机器学习（一）单、多变量线性回归与多项式回归

机器学习初步
机器学习，作为实现人工智能的一种方法，专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

简单的说，机器学习就是让计算机能根据已有的数据和经验，来优化自身的程序性能的研究方向。

打个比方，你在市场上买了一批芒果（训练数据），并记录下了它们的大小、颜色、产地、品种、采摘时间等相关信息（特征），然后开始品尝这些芒果的甜度（训练数据的输出变量），你或许会从这个过程中习得一些经验，并以此做出预测：在这家店买的颜色更黄，才摘下来不久的芒果（测试数据）会更好吃（测试数据的输出变量）。虽然这个预测不一定能做到100%的正确，但我们总能凭借着经验做出准确率十分高的预测，这也是我们希望计算机能够做到的一点。我们将训练数据提交给计算机，根据我们设计的模型，希望它能够找到一种特征与输出变量的映射关系（要求较好的拟合，同时避免过拟合的情况出现），就能让我们日后使用这个映射关系，根据输入的特征，预测一个输出变量。如果这个输出变量的预测与实际情况较其他模型而言相近（需要自行引入评价的指标，例如方差），我们就可以认为这是一个比较好的模型。

像上述这种通过我们给定的训练数据来给计算机“学习”，并进行预测的方法叫做监督学习，还有一种只是给计算机一个数据集，让它自行对这些数据的特征进行分类的方式被称为无监督学习，相较于监督学习，无监督学习更为贴近人类学习的方式，毕竟你永远不会为了教会一个孩子分辨老虎和狮子而给他看上成千上万张图片，而是让他自己发现两种动物的异同。除此以外，还有根据对外界环境反馈进行自我调整的机器学习方式被称作深度学习，例如平日里B站、淘宝上的推荐，就是根据你平常点击的习惯不断调整给你的推荐。

以上的是机器学习根据学习方法的不同的三种分类，当然还有一些比较模糊的分类（例如半监督学习）和其他的分类方式，在此不过多赘述。

接下来我们来讲讲机器学习的最简单的模型———线性回归模型

线性回归模型：单变量

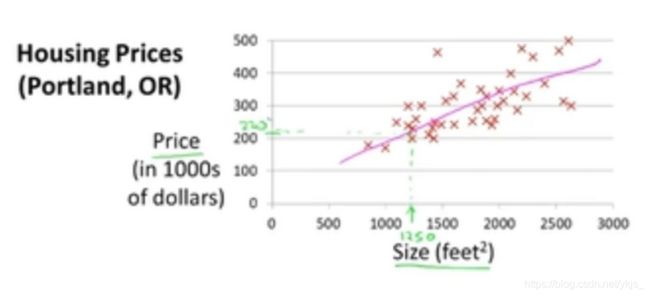
如上图，我们已知该地房价与房屋面积的一组数据，我们希望能构建一个函数让我们根据房屋的面积预测房屋价格。很简单地，我们希望这会是一个线性的模型，于是我们假设该地的房价与房屋面积有如下的关系（$h_{\theta }(x)$代表房价，x代表房屋面积）：

$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

那我们接下来的目标就是寻找这个函数关系中的${\theta }_0$和${\theta }_1$，使得我们做出的这条直线能够尽可能好地符合这组提供的数据，因此我们需要引入代价函数这个评价指标。

评价指标的选取可以多样化，你可以选取所有点到这条直线的距离之和，也可以选对于同一个面积，预测的房价减去实际的房价的差值的求和，但为了便于计算，我们选取如下的评价指标：

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
上式中的m代表训练集中有m组对应的数据，$x^{(i)}$代表训练集中第$i$个输入变量的取值，$y^{(i)}$代表训练集中第$i$个输出变量的取值，所以上式可以看作是平面上所有的点到给定直线的距离平方之和再乘上一个系数。为了让拟合的效果更好，我们想让$J({\theta }_0,{\theta }_1)$尽可能小，所以现在的问题就在于如何将$J({\theta }_0,{\theta }_1)$最小化。

面对数据量较小的数据集（小于10000条数据）时，采用暴力算法往往比较快，即对$J({\theta }_0,{\theta }_1)$求偏导
$$\frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_0}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$
$$\frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_1}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$

再令两偏导等于0
$$\frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_0}=0$$
$$\frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_1}=0$$
由数学上我们可以证明这个代价函数$J({\theta }_0,{\theta }_1)$是个凸函数，为此上述两个方程的解就是目标的${\theta }_0$和${\theta }_1$。

但对于数据量较大的数据集（大于10000条数据）时，暴力求解的速度就不是那么理想了。为此我们引入了梯度下降算法：先任取一组${\theta }_0$和${\theta }_1$，进行如下操作：
$${\theta }_0={\theta }_0-\alpha \frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_0}$$
$${\theta }_1={\theta }_1-\alpha \frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_1}$$
重复上两步操作直至$J({\theta }_0,{\theta }_1)$收敛（$J({\theta }_0,{\theta }_1)$是个凸函数保证了$J({\theta }_0,{\theta }_1)$若收敛则必定收敛于其最小值），此时的${\theta }_0$和${\theta }_1$就是我们要的目标。
该方法的思路就是找到一个让$J({\theta }_0,{\theta }_1)$下降最快的方向，并让这两个自变量按照这个方向一步步的移动，以达到最小的$J({\theta }_0,{\theta }_1)$。
注意：式子中给出的$\alpha$被称作学习率，用来控制${\theta }_0$和${\theta }_1$每一次改变量的大小，若$\alpha$过大，会导致$J({\theta }_0,{\theta }_1)$经过长时间的迭代后仍未发现收敛的迹象，若$\alpha$过小，则会使$J({\theta }_0,{\theta }_1)$达到目标结果的时间变长，为此，我们要根据处理的数据调整$\alpha$的大小。

多变量线性回归
以开头的芒果为例，影响其甜度的变量往往不止一个，现实中也是如此，为此我们需要引入多变量的线性回归。针对这个问题，我们只要对单变量的线性回归的公式略做修改：
$$h_{\theta }(x)=\theta x$$其中$\theta =({\theta }_0,{\theta }_1,\cdots ,{\theta }_n),x=(x_0,x_1,\cdots ,x_n),x_0=1$
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$其中$x^{(i)}$为第i个训练集中所有输入变量构成的向量，记该向量的第$j$个分量为$x_j^{(i)}$

由于$J(\theta )$是一个凸函数（不知道对不对的证明：关于代价函数为凸函数的证明）所以我们依然可以用求导法和梯度下降法来计算$\theta$这个向量，
求导法
$$\frac{\partial J(\theta )}{\partial {\theta }_i}=0,i=0,1,\cdots ,n$$梯度下降法
$${\theta }_i={\theta }_i-\alpha \frac{\partial J(\theta )}{\partial {\theta }_i},i=0,1,\cdots ,n$$
Python算法实现

def cost(theta,x,y):
    return sum((x*theta.T-y)*(x*theta.T-y).T)/(2*len(x))

def gradientdescent(theta,x,y):
    o=cost(theta,x,y)
    k=0
    for i in range(len(x)):
        theta[i]=theta[i]-a*sum(multipy(x*theta.T-y,x[:,i]))
    while (abs(cost(theta,x,y)-o)<0.0001 or k<10000):
        k=k+1
        o=cost(theta,x,y)
        for i in range(len(x)):
            theta[i]=theta[i]-a*sum(multipy(x*theta.T-y,x[:,i]))
    if (k==10000):
        print("请调整学习率")
    else:
        print("目标的theta取值为",theta)

在数据量过于庞大时，梯度下降算法的计算也显得较为复杂，为此，人们优化了梯度下降算法，提出了随机梯度下降算法，即每次只更新$\theta$中的一个分量，来达到梯度下降的效果。
随机梯度下降
$${\theta }_i={\theta }_i-\alpha \frac{\partial J(\theta )}{\partial {\theta }_i},随机取一个i$$

多项式回归
理解了上述的多变量回归，多项式回归理解起来就容易了。

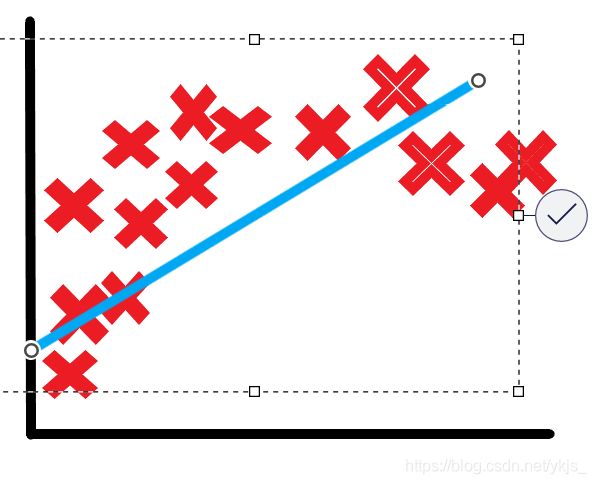
红色的是（房屋面积，房屋价格）的点列，蓝色是我们拟合的直线，可以发现，我们这条直线拟合的效果并不是很好，不少点离直线的距离有点远，这就是我们说的欠拟合。

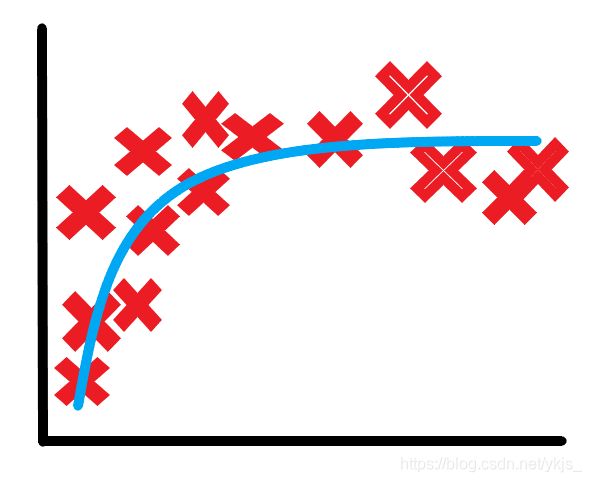
这张图中的曲线的拟合效果更好，如何得到这条曲线呢？
我们假设这条曲线的最高次数为n，房屋面积为$S$那么原本仅有一个特征的单变量线性回归，就可以增加$S^2,S^3,\cdots ,S^n$这$n-1$个特征，再使用多变量线性回归的方法处理即可。即使开始时有多个变量，也可以通过组成一般的多元$n$次多项式引入特征再用多元线性回归处理，这就是多项式回归的方法。

尽管多项式回归能很好地拟合你所提供的数据，但对这数据之外的其他数据其预测的效果就未必很好了，如上图就是一种给定的$n$比较大的情况，在图中所给的最后一个点之后，拟合的函数陡然上升，面积接近0的时候，拟合的函数陡然下降，这显然不符合生活实际。上图的情况就是我们常说的过拟合，因此，我们要学会控制多项式回归的最高次数以达到尽可能好的拟合效果。