基于SPSS的聚类分析原理概述
文章目录
- 1. 聚类分析的基本概念
-
- 1.1 方法概述
- 1.2 聚类方法
- 2. 系统聚类
-
- 2.1系统聚类的类型
- 2.2 两个距离概念
- 2.3亲疏程度的度量
-
- 2.3.1 个体间的亲疏程度的度量
- 2.3.2 个体与小类、小类与小类间的亲疏程度的度量
- 2.4 Transform Values and Measure
- 2.5 Statistics and Plots
- 3. K-均值聚类
-
- 3.1 K-均值聚类的操作界面
- 4. 聚类分析的注意点
1. 聚类分析的基本概念
在声音样本数目比较多的情况下,直接进行成对比较法,工作量非常大,且评价者容易疲劳,在很大程度上影响评价结果的一致性和准确性。对于这种情况,采用聚类分析,从 30 个声音样本中选择有代表性的样本进行主观评价试验,大大降低了主观评价试验的工作量1。
[1] 孙强. 基于人工神经网络的汽车声品质评价与应用研究[D]. 长春:吉林大学,2010.
1.1 方法概述
聚类分析是一种建立分类的方法,它能够将一批样本按照它们在性质上的亲疏程度在没有先验知识的情况下自动进行分类。这里,同一类中的个体有较大的相似性,不同类中的个体差异较大。
没有先验知识是指没有事先指定分类标准;亲疏程度是指在各变量(特征)取值上的总体差异程度。
1.2 聚类方法
SPSS软件中提供了3种聚类方法:
- Hierarchical Cluster Analysis 系统聚类法(又称层次聚类)
- K-Means Cluster Analysis K-均值聚类(又称快速聚类法)
- TwoStep Cluster Analysis 两步法聚类
2. 系统聚类
系统聚类法的基本思想是:
- 首先在聚类分析的开始,有多少样本就有多少类;
- 按照某种方法度量所有样本之间的亲疏程度,并把其中最亲密(或称最相似)的样本首先聚成一小类;
- 度量剩余的样本和小类间的亲疏程度,并将当前最亲密的样本或小类再聚成一类;
- 再度量剩余的样本和小类(或小类和小类)间的亲疏程度,并将当前最亲密的样本或小类再聚成一类;
- 如此反复,直到所有样本聚成一类为止。显然,越是后来合并的类,距离就越远。
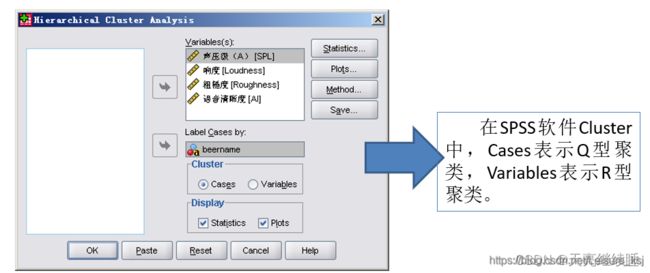
2.1系统聚类的类型
系统聚类有两种类型:
- 一是对样品聚类,称为Q型聚类;
- 二是对变量的聚类,称为R型聚类。
同时根据聚类过程不同,又分为分解法和凝聚法(SPSS软件的系统聚类采用的是凝聚法)。
2.2 两个距离概念
点和点之间的距离和类和类之间的距离。
- 点间距离有很多定义方式。最简单的是欧式距离,还有其他的距离。
- 当然还有一些和距离相反但起同样作用的概念,比如相似性等,两点相似度越大,就相当于距离越短。
- 由一个点组成的类是最基本的类;如果每一类都由一个点组成,那么点间的距离就是类间距离。但是如果某一类包含不止一个点,那么就要确定类间距离。
- 类间距离是基于点间距离定义的:比如两类之间最近点之间的距离可以作为这两类之间的距离,也可以用两类中最远点之间的距离作为这两类之间的距离;当然也可以用各类的中心之间的距离来作为类间距离。在计算时,各种点间距离和类间距离的选择是通过统计软件的选项实现的。不同的选择的结果会不同,但一般不会差太多。
2.3亲疏程度的度量
为了衡量样本间的亲疏程度,常用距离、匹配系数和相似系数作为度量标准。在SPSS中,对不同度量类型的数据采用了不同的测定亲疏程度的统计量。
2.3.1 个体间的亲疏程度的度量
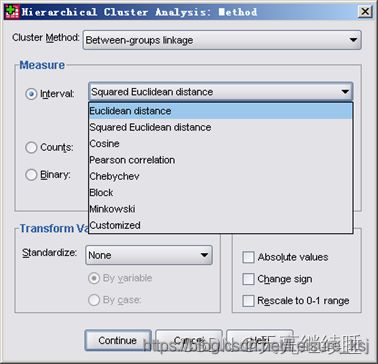
Measure(度量标准)
Interval(区间)——定距离变量个体间距离的计算公式,适用于R型聚类和Q型聚类。
-
Euclidean distance(欧氏距离)
d ( x , y ) = ∑ i ( x i − y i ) 2 d(x,y)=\sqrt{\sum_{i}(x_{i}-y_{i} )^{2}} d(x,y)=∑i(xi−yi)2 公式一 -
Squared Euclidean distance(平方欧氏距离)
d ( x , y ) = ∑ i ( x i − y i ) 2 d(x,y)=\sum_{i}(x_{i}-y_{i} )^{2} d(x,y)=∑i(xi−yi)2 公式二 -
Cosline(夹角余弦)
C x y ( 1 ) = cos θ x y = ∑ i x i y i ∑ i x i 2 ∑ i y i 2 C_{xy}(1)=\cos \theta _{xy} =\frac{\sum_{i}x_{i}y_{i}}{\sqrt{\sum_{i}x_{i}^{2}\sum_{i}y_{i}^{2}}} Cxy(1)=cosθxy=∑ixi2∑iyi2∑ixiyi 公式三 -
Pearson conelation(皮尔逊相关系数)
C x y ( 2 ) = γ x y = ∑ i ( x i − x ˉ ) ( y i − y ˉ ) ∑ i ( x i − x ˉ ) 2 ∑ i ( y i − y ˉ ) 2 C_{xy}(2)=\gamma _{xy} =\frac{\sum_{i}(x_{i}-\bar{x})(y_{i}-\bar{y} )}{\sqrt{\sum_{i}(x_{i}-\bar{x})^{2}\sum_{i}(y_{i}-\bar{y} )^{2}}} Cxy(2)=γxy=∑i(xi−xˉ)2∑i(yi−yˉ)2∑i(xi−xˉ)(yi−yˉ) 公式四 -
Chebychev(切比雪夫距离)
d ( x , y ) = M a x i ∣ x i − y i ∣ d(x,y)=\underset{i}{Max}\left | x_{i}-y_{i} \right | d(x,y)=iMax∣xi−yi∣ 公式五 -
Block(曼哈顿距离)
d ( x , y ) = ∑ i ∣ x i − y i ∣ d(x,y)=\sum_{i}\left | x_{i}-y_{i} \right | d(x,y)=∑i∣xi−yi∣ 公式六 -
Minkowski(闵科夫斯基距离)
d ( x , y ) = [ ∑ i ∣ x i − y i ∣ q ] 1 q d(x,y)=\left [ \sum_{i}\left | x_{i}-y_{i} \right | ^{q} \right ] ^{\frac{1}{q} } d(x,y)=[∑i∣xi−yi∣q]q1 公式七 -
Customized(自定义距离)
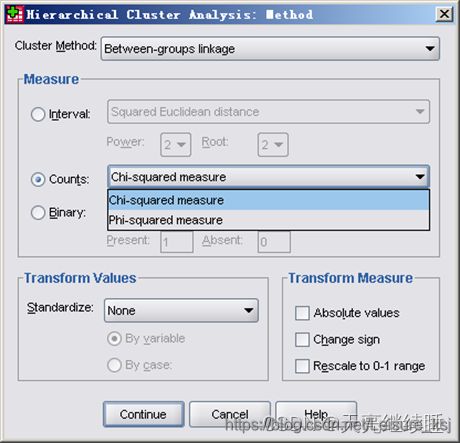
如果所涉及的个变量都是计数的非连续变量,对计数变量的不相似性测度方法,是根据被计算的两个观测量或两个变量总额数计算其不相似性。期望值来自观测量或变量的独立模型。
个体间距离定量的方式:
- Chi-square measure(卡方测度):用卡方值测度不相似性。系统默认选项。
- Phi-square measure(Phi方测度):两组频数之间的Ф2 测度。
Binary(二值变量)——二值变量个体间距离的计算公式
如果所涉及的定义通常都是二值变量,那么个体间距离的定义通常有简单匹配系数(Simple matching)和雅科比系数(Jaccard)两种方式。
2.3.2 个体与小类、小类与小类间的亲疏程度的度量
概念:不同类中两个最近的点之间的距离。
特点:对噪声和离群点很敏感。
公式: D p q = min d ( x i , x j ) D_{pq}=\min d\left ( x_{i},x_{j} \right ) Dpq=mind(xi,xj) 公式八
概念:不同类中两个最远的点之间的距离。
特点:对噪声和离群点不是很敏感,倾向于分裂较大的类。
公式: D p q = max d ( x i , x j ) D_{pq}=\max d\left ( x_{i},x_{j} \right ) Dpq=maxd(xi,xj) 公式九
- Centroid clustering (质心聚类法)
公式: D p q = min d ( x p ˉ , x q ˉ ) D_{pq}=\min d\left ( \bar{x_{p}} ,\bar{x_{q}} \right ) Dpq=mind(xpˉ,xqˉ) 公式十
- Ward’s method (离差平方和法)
公式:
D 1 = ∑ x i ∈ G p ( x i − x p ˉ ) ′ ( x i − x p ˉ ) D_{1} =\sum_{x_{i}\in G_{p}}(x_{i}-\bar{x_{p}} )'(x_{i}-\bar{x_{p}} ) D1=∑xi∈Gp(xi−xpˉ)′(xi−xpˉ) 公式十一
D 2 = ∑ x j ∈ G q ( x j − x q ˉ ) ′ ( x j − x q ˉ ) D_{2} =\sum_{x_{j}\in G_{q}}(x_{j}-\bar{x_{q}} )'(x_{j}-\bar{x_{q}} ) D2=∑xj∈Gq(xj−xqˉ)′(xj−xqˉ) 公式十二
D 1 + 2 = ∑ x k ∈ G p ∪ G q ( x k − x ˉ ) ′ ( x i − x ˉ ) ⇒ D p q = D 1 + 2 − D 1 − D 2 D_{1+2} =\sum_{x_{k}\in G_{p}\cup G_{q}}(x_{k}-\bar{x} )'(x_{i}-\bar{x})\Rightarrow D_{pq}=D_{1+2}-D_{1}-D_{2} D1+2=∑xk∈Gp∪Gq(xk−xˉ)′(xi−xˉ)⇒Dpq=D1+2−D1−D2 公式十二
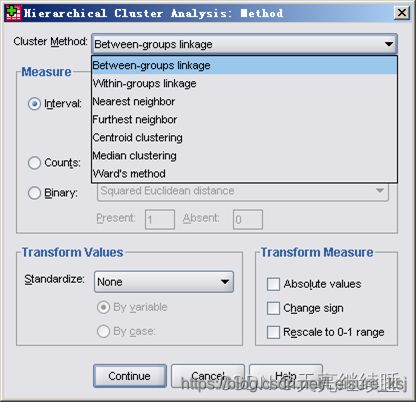
-
Between-groups linkage (组间联接法)
-
Within-groups linkage (组内联接法)
-
Median clustering (中位数聚类法)
一般情况下,用不同的方法聚类的结果是不会完全一致的。在实际应用中,一般采用以下两种处理方法:
- 根据分类问题本身的专业知识结合实际需要来选择分类方法,并确定分类个数;
- 多用几种分类方法去作,把结果中的共性提出来,对有争议的样本用判别分析去归类。
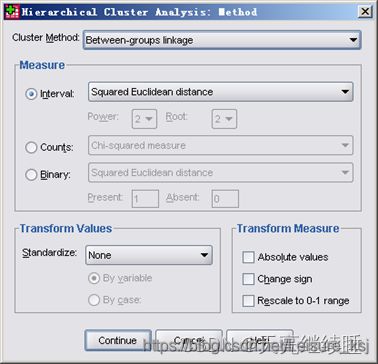
2.4 Transform Values and Measure
Transform Values(转换值)
SPSS软件中,提供了将数据标准化的方法。注意只有等间隔测度的数据(选择Interval)或计数数据(选择Counts)才可以进行标准化。
- None:不进行标准化(系统默认值)。
- Z scores:数据标准化到Z 分数,标准化后变量均值为0,标准差为 1。
- Range -1 to 1:把数据标准化到-1 到+1 范围内。
- Range 0 to 1:把数据标准化到0 到+1 范围内。
- Maximum Magnitude of 1:把数据标淮化到最大值为1。表示各变量除以最大值。
- Mean of 1:把数据标准化到均值为1。表示各变量除以均值。
- Standard deviation of 1:把数据标准化到标准差为1。表示各变量除以标准差。
Transform Measure(转换方法)
- Absolute Values:把距离值取绝对值。
- Change sign:把相似性值变为不相似性值或相反。
- Rescale bo 0~1 range:重新调整测度值到范围0~l。
2.5 Statistics and Plots
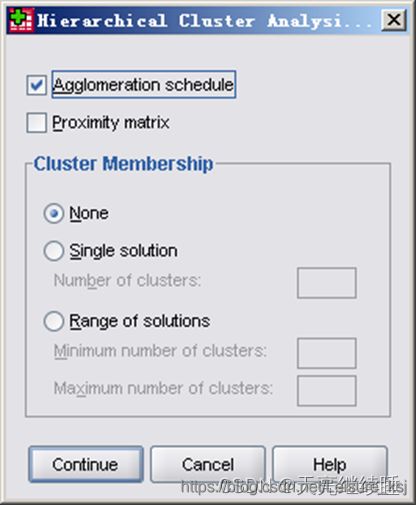
Agglomeration schedule(合并进程表):显示聚类过程中每一步合并的类或观测量,反映聚类过 程中每一步样品或类的合并过程(系统默认选项)。
Proximity matrix(相似性矩阵):输出各类之间的距离矩阵。
Cluster Membership(聚类成员):显示每个样本被分派到的类或显示若干步凝聚过程,其中:
- None(无):不显示类成员表,系统默认选项。
- Single solution(单一方案):选择此项并在对应的(Number of clusters(聚类数)参数框中指定分类数。例如指输入数字“4”,则会在输出窗中显示聚为 4类的分析结果。
- Range of solutions(方案范围):选择此选项并在下边的Mi nimum number of clusters(最小聚类数)和Maxmum number of clusters(最大聚类数)参数框中输入最小聚类数目和最大聚类数目。表示分别输出样品或变量的分类数从最小值到最大值的各种分 类聚类表。输入的两个数值必须是不等于1 的正整数,最大类数值不 能大于参与聚类的样品数或变量总数。
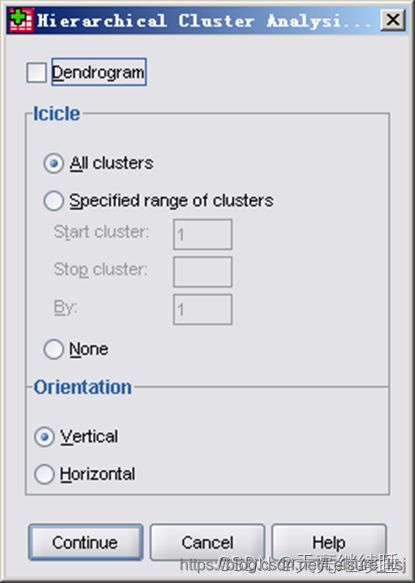
Dendrogram(树状图):显示树形图。
Icicle(冰柱):显示冰柱图形,其中:
- All clusters:显示全部聚类结果的冰柱图。
- Specified range clusters:限定显示的聚类范围。例如,输入的结果是:3,9,2,生成的冰柱图从第三步开 始,显示第三、五、七、九步聚类的情况。
- None:不生成冰柱图。
Orientation(方向):冰柱图的显示方向
- Vertical:纵向显示的冰柱图。
- Horizontal:横向显示的冰柱图。
3. K-均值聚类
系统聚类无需事先确定聚成多少类,但k-均值聚类却要求事先确定聚成多少类:
- 首先由用户指定需要聚成多少类(假定聚成3类);
- 然后,确定3个初始类的中心。有两种方式:一是用户指定方式,二是通过SPSS软件自动确定初始类的中心。
- 然后,根据距离最近原则进行分类。计算每个样本到这3类中心点的距离,把各个样本按照距离最近的原则归入这3类中。
- 这样,3类中可能由若干个样本,重新计算这3类的中心。 按照新的中心位置,重新计算每个样本距离新的3类中心点的距离,并重新进行归类。
- 如此叠代下去,直到达到停止叠代的要求。
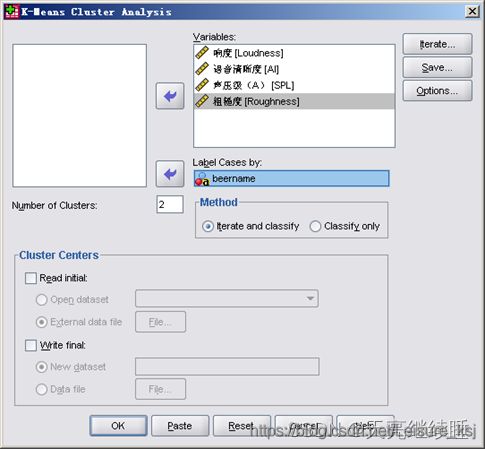
3.1 K-均值聚类的操作界面
Method(方法):指定聚类过程是否调整类中心点。
- Iterate and classify——表示在聚类分析的每一步都重新确定类中心点;
- Classify only——表示聚类分析过程中类中心点始终为初始类中心点,此时仅一次迭代。
Cluster Centers(类中心)
- Read initial——表示使用指定数据文件中的样本作为初始类中心;
- Write final——表示把聚类结果中的各类数据保存到指定的文件中。
Number of Clusters(确定聚类数目):应小于样本数。
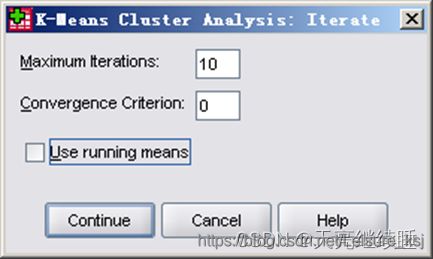
迭代参数的设置
- Maximum Iterations:输入最大迭代次数。当达到迭代次数上限时,即使没有满足收敛判据,迭代也停止。系统默认值为10。选择范围为1~999。
- Convergence Criterion:指定收敛标准,输入一个不超过1的正数作为判定迭代收敛的标准。系统缺省的收敛标准是0.02,表示当两次迭代计算的最小的类中心的变化距离小于初始类中心距离的2%时迭代停止。
- Use running means:表示在每个样本被分配到一类后立刻计算新的类中心。如果不选择此项,则在完成了所有样本的一次分配后再计算各类的类中心,这样可以节省迭代时间。
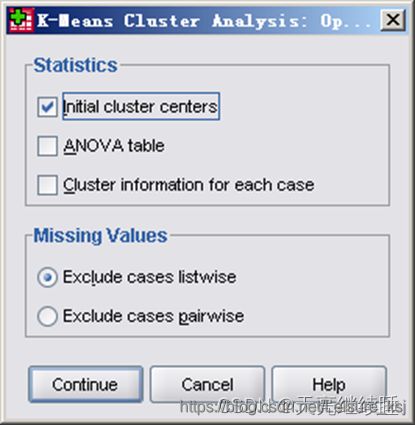
其他选项输出:
- Statistics(统计量)——选择输出统计量。
- Initial cluster centers:初始聚类中心。
- ANOVA table:表示以聚类分析产生的类为控制变量,以个变量为样本变量进行单因素分析,并输出各个变量的方差分析表。
- Cluster information for each case:显示每个观测量的聚类信息。
- Missing Values(缺失值)——选择处理缺失值方法。
- Exclude cases listwise:将出现在Variables变量表中变量带有缺失值的样本从分析中剔除。
- Exclude cases pairwise:只有当一个观测量的全部聚类变量值均缺失时才将其从分析中剔除,否则,根据所有其他非缺失变量值把它分配到最近的一类中去。
4. 聚类分析的注意点
- 聚类结果主要受所选择的变量影响。如果去掉一些变量,或者增加一些变量,结果会很不同。因此可根据实际工作经验和研究问题的特征人为的选择变量,这些变量应该和分析的目标密切相关,反映分类对象的特征。
- 各变量的变量值不应有数量级上的差异,因此为了避免对变量单位选择的依赖,数据应当标准化。
- 各变量间不应有较强的线性相关关系。
- 相比之下,聚类方法的选择则不那么重要。因此,聚类之前一定要目标明确。
- 另外就分成多少类来说,也要有道理。只要你高兴,可以得到任何可能数量的类。但是,聚类的目的是要使各类距离尽可能的远,而类中各点的距离尽可能的近,而且分类结果还要有令人信服的解释。这一点就不是数学可以解决的了。
1 ↩︎