谣言检测文献阅读四—Reply-Aided Detection of Misinformation via Bayesian Deep Learning
系列文章目录
- 谣言检测文献阅读一—A Review on Rumour Prediction and Veracity Assessment in Online Social Network
- 谣言检测文献阅读二—Earlier detection of rumors in online social networks using certainty‑factor‑based convolutional neural networks
- 谣言检测文献阅读三—The Future of False Information Detection on Social Media:New Perspectives and Trends
- 谣言检测文献阅读四—Reply-Aided Detection of Misinformation via Bayesian Deep Learning
- 谣言检测文献阅读五—Leveraging the Implicit Structure within Social Media for Emergent Rumor Detection
- 谣言检测文献阅读六—Tracing Fake-News Footprints: Characterizing Social Media Messages by How They Propagate
- 谣言检测文献阅读七—EANN: Event Adversarial Neural Networks for Multi-Modal Fake News Detection
- 谣言检测文献阅读八—Detecting breaking news rumors of emerging topics in social media
文章目录
- 系列文章目录
- 前言
- 1 介绍
- 2 相关工作
-
- 2.1 文本内容
- 2.2 来源可信度分析
- 2.3 多媒体功能
- 2.4 社会参与
- 3 问题说明
- 4 贝叶斯深度学习
-
- 4.1对声明进行编码
- 4.2 对人们的回复进行编码
- 4.3 准确性建模
- 5 优化
-
- 5.1 推理模型
- 5.2 目标函数
- 5.3 梯度估计
- 5.4 预测
- 6 实验设置
-
- 6.2 数据集
- 6.4 超参数设置
- 7 结果与讨论
-
- 7.2 潜在分布的合并是否优于确定性分布?
- 7.3 从人们的回复中获得的辅助信息是否会产生一种更准确的后验信念,即声明的真实性?
- 7.4 在对回复进行编码时,时间顺序是否优于随机顺序?
- 7.5 加入一个潜在变量来编码回复是否有益?
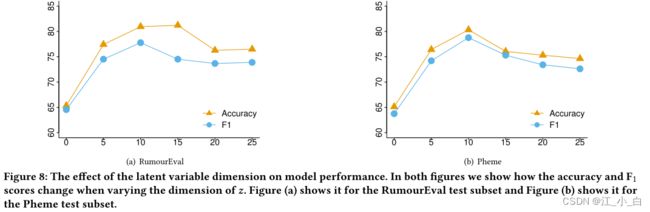
- 7.6 潜在变量z的维数如何影响模型的性能?
前言
文章:Reply-Aided Detection of Misinformation via Bayesian Deep Learning
发表会议:2019 IW3C2 (International World Wide Web Conference Committee)
时间:2019年5月
1 介绍
1、文章说目前其他的文章存在的一个问题:这些模型的一个主要限制是它们无法表示由有关正在审查的声明的不完整或有限的可用数据引起的不确定性。(A major limitation of these models is their inability to represent uncertainty caused by incomplete or finite available data about the claim being examined.)
2、使用原贴信息和评论信息两部分
3、提出了一种随机梯度变分贝叶斯(SGVB)算法,推导了模型的易处理下限(ELBO)目标函数,以逼近难以处理的分布。该模型沿着最大化ELBO目标函数的方向进行优化。
4、优越之处
- 由于不完整/有限的可用数据而导致的不确定性的有效表示
- 基于时间顺序的方法从人们的回复中提取辅助信息;
- 一种推断潜在分布的 SGVB 算法;
- 我们的模型在两个真实世界数据集上的系统实验。
2 相关工作
2.1 文本内容
包含语言特征,因为虚假信息不是为了叙述客观事实,因此它们通常包含固执己见或煽动性的语言
2.2 来源可信度分析
原始发帖者诚信度越高、专业知识越渊博发帖的真实率越高(诚信度和专业知识可以通过账户特征来评估,例如个人信息的完整性、关注者和粉丝的数量)
2.3 多媒体功能
通过多媒体的视觉特征和统计特征判断信息的真假。视觉特征包括清晰度得分、连贯性得分、多样性得分和聚类得分。统计特征包括计数、图像比率、多图像比率、热图像比率、长图像比率等
2.4 社会参与
人群的智慧,即通过其他人对于原贴的态度,立场,支持、反对、中性
3 问题说明
声明 C = { c 1 , c 2 , . . . , c N } C=\{c_1,c_2,...,c_N\} C={c1,c2,...,cN}, c i c_i ci由一 M M M个用户的回复 D = { d 1 , d 2 , . . . , d M } D=\{d_1,d_2,...,d_M\} D={d1,d2,...,dM}组成,其中需要判断的消息为 { c i , D i } \{c_i,D_i\} {ci,Di},标签为 y i y_i yi
4 贝叶斯深度学习
4.1对声明进行编码
通过对声明编码得到先验概率,声明 c = { w 1 , w 2 , . . . , w l } c=\{w_1,w_2,...,w_l\} c={w1,w2,...,wl},其中 w l ∈ R d w_l\in \mathbb{R}^d wl∈Rd是一个 d d d维向量
![]()
![]() 其中 p p p是一个潜在分布, θ θ θ表示 h c h_c hc的非线性变换,以生成 p p p的参数。这种非线性变换对于捕获 h c h_c hc的更高级别表示至关重要;我们通过多层感知器(MLP)实现这种非线性变换。
其中 p p p是一个潜在分布, θ θ θ表示 h c h_c hc的非线性变换,以生成 p p p的参数。这种非线性变换对于捕获 h c h_c hc的更高级别表示至关重要;我们通过多层感知器(MLP)实现这种非线性变换。
我们假设潜变量z是连续的,服从多元高斯分布。变量z的参数化如下:
![]() 其中, μ θ μ_θ μθ和 d i a g ( σ θ 2 ) diag(σ^2_θ) diag(σθ2)是多元高斯分布的均值和协方差矩阵。由于变量 z z z取决于声称的隐藏状态 h c h_c hc,我们通过深层神经网络从 h c h_c hc推导出高斯分布的这两个参数:
其中, μ θ μ_θ μθ和 d i a g ( σ θ 2 ) diag(σ^2_θ) diag(σθ2)是多元高斯分布的均值和协方差矩阵。由于变量 z z z取决于声称的隐藏状态 h c h_c hc,我们通过深层神经网络从 h c h_c hc推导出高斯分布的这两个参数:

其中 f θ f_θ fθ表示一个MLP, l 1 l_1 l1和 l 2 l_2 l2表示两个线性变换(LT)。因为LT可以产生负值,为了产生 σ θ σ_θ σθ,我们将 l 2 l_2 l2的结果指数化。
为了使 μ θ μ_θ μθ和 σ θ σ_θ σθ可微,并通过潜在分布 ( p ) (p) (p)反向传播损失,使用以下重新参数化技巧:
![]() 其中 0 0 0是零向量, I I I是单位矩阵。通过使用潜变量 z z z,我们的模型能够捕获数据中复杂的噪声模式。
其中 0 0 0是零向量, I I I是单位矩阵。通过使用潜变量 z z z,我们的模型能够捕获数据中复杂的噪声模式。
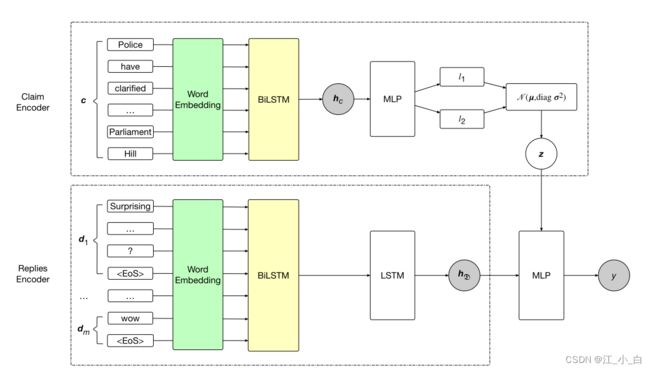
4.2 对人们的回复进行编码
我们现在展示人们的回复编码器来获取辅助信息。该辅助信息是特定于声明的,用于通过纠正声明真实性的先验信念来生成后验信念。
社交媒体平台上的回复按时间线列出,最早的回复显示在列表顶部。随着更多证据的出现,关于事件的真相可以逐渐显现,因此我们假设最新的回复往往比早期的回复更可靠、更重要。基于这个假设,我们设计了一个两层循环神经网络来编码回复:第一层应用 BiLSTM 来总结每个回复的语义信息,第二层应用 LSTM 来捕捉回复的时间语义变化.
![]() h d m h_{d_m} hdm 是回复 d m d_m dm 的摘要
h d m h_{d_m} hdm 是回复 d m d_m dm 的摘要
为了捕获所有回复的语义信息,我们将每个回复的串联隐藏状态依次输入到 LSTM 中。我们使用 LSTM 而不是 BiLSTM,因为前者对最近的输入赋予了很高的权重,这符合我们对最新回复的相对重要性的假设。具体来说,LSTM 以顺序方式将每个回复的隐藏状态作为输入:
![]() 其中 h d M = { h d 1 , . . . , h d m , . . . , h d M } h^M_d = \{h_{d_1}, . . . ,h_{d_m} , . . . ,h_{d_M}\} hdM={hd1,...,hdm,...,hdM}
其中 h d M = { h d 1 , . . . , h d m , . . . , h d M } h^M_d = \{h_{d_1}, . . . ,h_{d_m} , . . . ,h_{d_M}\} hdM={hd1,...,hdm,...,hdM}
最后一个隐藏状态 h D h_D hD 包含每个回复的语言信息和回复之间沿时间线的语义变化。然后,该 h D h_D hD 用于通过纠正声明真实性的先验信念来生成后验信念。
4.3 准确性建模
后验信念是通过 MLP 组合声明和回复信息来生成的。 MLP 的强非线性使其适合于查找索赔与其答复之间的复杂关系。具体来说,MLP 输入是潜在声明变量 z 连接到回复的隐藏状态 h D h_D hD
![]()
5 优化
我们模型的随机变量是非线性和非共轭的。因此,后验分布不能通过分析推导出来。为了逼近后验分布,我们构建了一个由 ϕ \phi ϕ 参数化的推理模型来逼近难以处理的真实后验 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc);然后我们推导出一个目标函数来衡量 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc)的逼近程度;最后,我们利用随机梯度变分贝叶斯 (SGVB) 方法来学习推理模型参数 ϕ \phi ϕ和生成模型参数 θ θ θ。
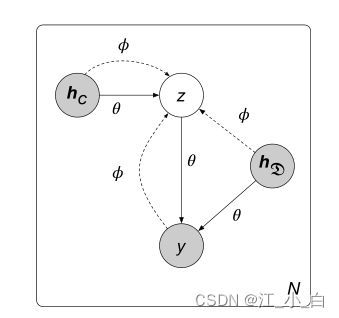 灰色节点代表观察变量,而空白节点代表潜在变量。实线表示生成模型 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc)、 p ( y ∣ z , h D ) p(y|z,h_D) p(y∣z,hD),虚线表示变分逼近 q ϕ ( z ∣ y , h c , h D ) q_\phi(z|y,h_c,h_D) qϕ(z∣y,hc,hD) 到难以处理的后验 p θ ( z ∣ h c ) p_θ (z|h_c) pθ(z∣hc)。变分参数与生成模型参数一起学习。
灰色节点代表观察变量,而空白节点代表潜在变量。实线表示生成模型 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc)、 p ( y ∣ z , h D ) p(y|z,h_D) p(y∣z,hD),虚线表示变分逼近 q ϕ ( z ∣ y , h c , h D ) q_\phi(z|y,h_c,h_D) qϕ(z∣y,hc,hD) 到难以处理的后验 p θ ( z ∣ h c ) p_θ (z|h_c) pθ(z∣hc)。变分参数与生成模型参数一起学习。
5.1 推理模型
遵循神经变分推理方法,我们构建了一个由 ϕ \phi ϕ 参数化的推理模型,以计算近似的后验分布,称为变分分布。给定观察到的变量,我们定义了一个变分分布 q ϕ ( z ∣ y , h c , h D ) q_\phi(z|y,h_c,h_D) qϕ(z∣y,hc,hD) 来逼近真实的后验分布 p θ ( z ∣ h c ) p_θ (z|h_c) pθ(z∣hc)。类似于变分自动编码器(VAE),类似于方程式。 公式(3) 对于 p θ ( z ∣ h c ) p_θ (z|h_c) pθ(z∣hc),变分分布被选择为多元高斯分布:
![]() 其中 µ ϕ µ_ϕ µϕ 和 d i a g ( σ ϕ 2 ) diag(σ^2_ϕ ) diag(σϕ2) 是多元高斯分布的均值和协方差矩阵。我们使用深度神经网络从观察到的变量中推导出这两个参数:
其中 µ ϕ µ_ϕ µϕ 和 d i a g ( σ ϕ 2 ) diag(σ^2_ϕ ) diag(σϕ2) 是多元高斯分布的均值和协方差矩阵。我们使用深度神经网络从观察到的变量中推导出这两个参数:
 其中 f ϕ f_ϕ fϕ 表示一个 MLP, l 3 l_3 l3 和 l 4 l_4 l4 表示两个 LT。请注意,在计算 µ µ µ和 l o g σ log σ logσ的推理模型中,我们使用 y , h c , h D y,h_c,h_D y,hc,hD 而不仅仅是生成模型中的 h c h_c hc。
其中 f ϕ f_ϕ fϕ 表示一个 MLP, l 3 l_3 l3 和 l 4 l_4 l4 表示两个 LT。请注意,在计算 µ µ µ和 l o g σ log σ logσ的推理模型中,我们使用 y , h c , h D y,h_c,h_D y,hc,hD 而不仅仅是生成模型中的 h c h_c hc。
5.2 目标函数
下面我们根据变分原理推导出贝叶斯深度学习模型的目标函数。为了最大化对数似然 l n ( p ( y ∣ h c , h D ) ) ln(p(y|h_c,h_D)) ln(p(y∣hc,hD)) ,我们推导出一个证据下界 (ELBO) 目标函数,以确保正确逼近真实的后验。为了简化目标函数推导的符号,我们进行以下代入: p θ ( y ) = p θ ( y ∣ z , h D ) , p θ ( z ) = p θ ( z ∣ h c ) , q ϕ ( z ) = q ϕ ( z ∣ y , h c , h D ) p_θ (y) = p_θ (y|z,h_D), p_θ (z) = p_θ (z|h_c ), q_ϕ (z) =q_ϕ(z|y,h_c,h_D) pθ(y)=pθ(y∣z,hD),pθ(z)=pθ(z∣hc),qϕ(z)=qϕ(z∣y,hc,hD)-公式(10)。目标函数推导如下:

其中 L ( θ , ϕ ∣ y , h c , h D ) L(θ, ϕ|y,h_c,h_D) L(θ,ϕ∣y,hc,hD) 是 ELBO 目标函数。通过使用 Jensen 不等式,推导的第二行是可能的。由于 ELBO 目标函数是对数似然 l n ( p ( y ∣ h c , h D ) ) ln(p(y|h_c,h_D)) ln(p(y∣hc,hD)) 的下界,因此其最大化最大化对数似然。
- 关于ELBO这篇文章和这篇文章写的很清楚,还有代码
- 变分自编码器,这篇文章写的很清楚
5.3 梯度估计
我们推导出一个基于小批量的 SGVB 估计器来区分和优化关于推理参数 ϕ ϕ ϕ和生成参数 θ θ θ的ELBO 目标函数 L ( θ , ϕ ∣ y , h c , h D ) L(θ, ϕ|y,h_c,h_D) L(θ,ϕ∣y,hc,hD)。通过蒙特卡罗估计,我们计算了 ELBO 目标函数的期望部分。让小批量大小为 B,对于每个声明 c i , i ∈ [ 1 , B ] c_i,i ∈ [1, B] ci,i∈[1,B],S 是从变分后验分布 z ~ ∼ q ϕ \widetilde{z} ∼ q_ϕ z ∼qϕ中抽取的样本。给定一个声明子集,我们可以为基于小批量的完整数据集构建一个 ELBO 目标函数的估计器,如下所示:
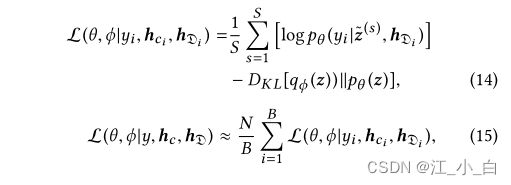 其中 L ( θ , ϕ ∣ y i , h c i , h D i ) L(θ, ϕ|y_i,h_{c_i} ,h_{D_i} ) L(θ,ϕ∣yi,hci,hDi)表示基于第 i 个声明的估计值,N 是声明总数。算法 1 显示了生成 (θ) 和推理 (ϕ) 参数的小批量梯度下降优化过程。请注意,算法 1 中的梯度步骤可以很容易地与更强大的优化器交替使用,例如 Adam 算法。尽管 q ϕ ( z ∣ y , h c , h D ) q_ϕ (z|y,h_c,h_D) qϕ(z∣y,hc,hD) 和 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc) 都被建模为参数化高斯分布。前者是后者的近似值,仅在学习期间起作用。相反,后者是生成样本的学习分布,以便对声明的真实性进行分类。
其中 L ( θ , ϕ ∣ y i , h c i , h D i ) L(θ, ϕ|y_i,h_{c_i} ,h_{D_i} ) L(θ,ϕ∣yi,hci,hDi)表示基于第 i 个声明的估计值,N 是声明总数。算法 1 显示了生成 (θ) 和推理 (ϕ) 参数的小批量梯度下降优化过程。请注意,算法 1 中的梯度步骤可以很容易地与更强大的优化器交替使用,例如 Adam 算法。尽管 q ϕ ( z ∣ y , h c , h D ) q_ϕ (z|y,h_c,h_D) qϕ(z∣y,hc,hD) 和 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc) 都被建模为参数化高斯分布。前者是后者的近似值,仅在学习期间起作用。相反,后者是生成样本的学习分布,以便对声明的真实性进行分类。

5.4 预测
训练后,我们通过生成网络计算后验分布 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc)。声明真实性的实际预测是通过对 S 个样本的期望给出的:
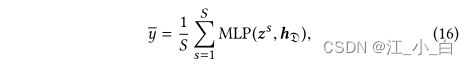 其中 z s z^s zs 表示从真实后验分布 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc) 中抽取的样本
其中 z s z^s zs 表示从真实后验分布 p θ ( z ∣ h c ) p_θ (z|h_c ) pθ(z∣hc) 中抽取的样本
6 实验设置
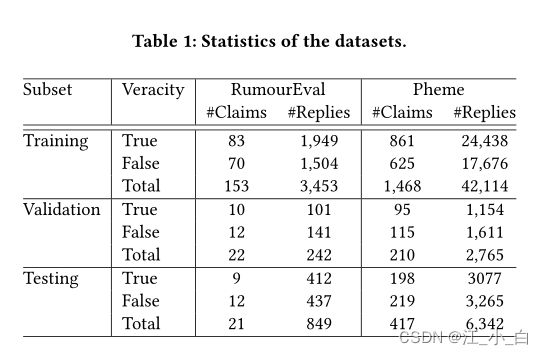
6.2 数据集
6.4 超参数设置
三个 LSTM 的激活函数是 tanh。 MLP 的激活函数是 ReLu。在验证子集上调整的超参数是:
- 所有三个 LSTM 的隐藏层的维度都是 30;
- 潜在变量的维数为 10;
- minibatch 大小为 32;
- Monte Carlo 估计中使用的样本数为 20。
Dropout 用于改进神经网络训练,L2 范数正则化被应用于神经网络的权重,优化器采用Adam。
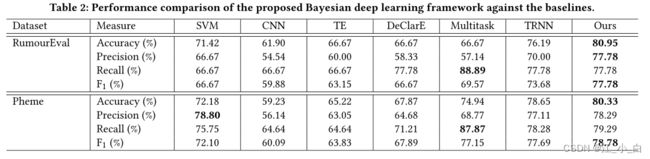
7 结果与讨论
7.2 潜在分布的合并是否优于确定性分布?
在本小节中,我们评估了在声明编码器中使用潜在分布对错误信息检测任务的影响。为了评估潜在分布p的影响,我们在我们的模型中去除p,并将其分类性能与完整模型进行比较。具体来说,去除p是通过获取BiLSTM隐藏状态的输出,即 h c h_c hc,并将其作为输出MLP的输入来完成的。模型的其余部分保持不变。由于不涉及潜在分布,去除p的模型根据传统的Softmax损耗最小化进行了优化。在图4(a)和图4(b)中,我们展示了在Rumoreval和Pheme测试子集上去除p的模型相对于完整模型的分类性能。我们观察到,在每个评估指标上,完整模型的表现都比烧蚀模型好至少7.77%。这表明通过使用潜在分布可以获得更好的表示质量。

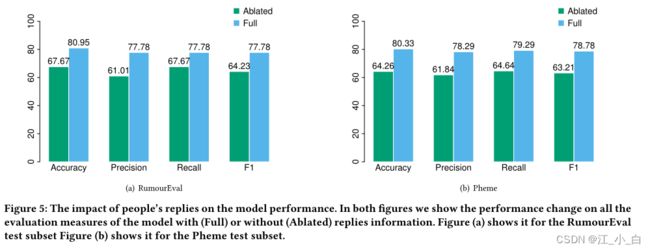
7.3 从人们的回复中获得的辅助信息是否会产生一种更准确的后验信念,即声明的真实性?
7.4 在对回复进行编码时,时间顺序是否优于随机顺序?
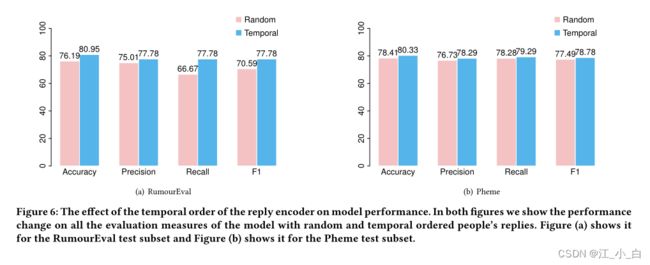 对于RumorEval数据集影响较大,但是对于Pheme数据集影响较小,而RumorEval数据量(153)远远小于Pheme(1468),推测是否是和数据量有关,是否是当原始数据量大时候回复的影响几乎消失
对于RumorEval数据集影响较大,但是对于Pheme数据集影响较小,而RumorEval数据量(153)远远小于Pheme(1468),推测是否是和数据量有关,是否是当原始数据量大时候回复的影响几乎消失
7.5 加入一个潜在变量来编码回复是否有益?
我们通过在回复编码器中添加一个新的潜在分布来扩展我们的模型。与声明编码器所做的类似,新的潜在分布被设计为多维高斯分布,其均值和协方差矩阵源自 LSTM 输出 h D h_D hD(如公式 3、4 和 5 中所示)。与等式 6 类似地对一个新的潜在变量进行采样,并将其输入到 MLP 以预测正在检查的声明的准确性。实验证明,回复添加额外的潜在分布并没有提供任何额外的性能改进。
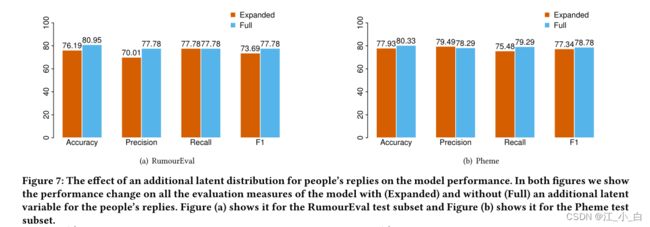 文章说没有影响,但是对于性能的提升,甚至比回复顺序在树枝上影响更大,不知道为什么时间顺序说有影响,这个又说没有影响
文章说没有影响,但是对于性能的提升,甚至比回复顺序在树枝上影响更大,不知道为什么时间顺序说有影响,这个又说没有影响