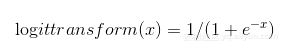《Python机器学习——预测分析核心算法》——2.4 基于因素变量的实数值预测：鲍鱼的年龄...

本节书摘来异步社区《Python机器学习——预测分析核心算法》一书中的第2章，第2.4节，作者：【美】Michael Bowles（鲍尔斯），更多章节内容可以访问云栖社区“异步社区”公众号查看。

2.4　基于因素变量的实数值预测：鲍鱼的年龄

探测未爆炸的水雷数据集的工具同样可以用于回归问题。在给定物理测量值的情况下，预测鲍鱼的年龄就是此类问题的一个实例。鲍鱼的属性中包括因素属性，下面将说明属性中含有因素属性后与上例有什么不同。

鲍鱼数据集的问题是根据某些测量值预测鲍鱼年龄。当然可以对鲍鱼进行切片，然后数年轮获得鲍鱼年龄的精确值，就像通过数树的年轮得到树的年龄一样。但是问题是这种方法代价比较大，耗时（需要在显微镜下数年轮）。因此更方便经济的方法是做些简单的测量，如鲍鱼的长度、宽度、重量等指标，然后通过一个预测模型对其年龄做相对准确的预测。预测分析有大量的科学应用，学习机器学习的一个好处就是可以将其应用到一系列很有趣的问题上。

鲍鱼数据集可以从UC Irvine数据仓库中获得，其URL是http://archive.ics.uci.edu/ml/machine-learning-database/abalone/abalone.data。此数据集数据以逗号分隔，没有列头。每个列的名字存在另外一个文件中。代码清单2-11将鲍鱼数据集读入Pandas数据框，然后进行分析，这些分析与“分类问题：用声纳探测未爆炸的水雷”节中的一样。由数据的性质决定的，“岩石vs.水雷”数据集的列名（属性名）更加通用。为了能够从直觉上判断提出的预测模型是否可接受，理解鲍鱼数据集各个列名（属性名）的意义是十分重要的。因此，在代码中将列名（属性名）直接拷贝到代码中，与相关的数据绑定在一起，帮助直接感受下一步机器学习算法应该怎么预测。建立预测模型所需的数据包括性别、长度、直径、高度、整体重量、去壳后重量、脏器重量、壳的重量、环数。最后一列“环数”是十分耗时采获得的，需要锯开壳，然后在显微镜下观察得到。这是一个有监督机器学习方法通常需要的准备工作。基于一个已知答案的数据集构建预测模型，然后用这个预测模型预测不知道答案的数据。

代码清单2-11不仅展示了产生统计信息的代码，而且展示了打印输出的统计信息。第一部分打印数据集的头和尾。为了节省空间只显示了头。当你自己运行代码时，就可以看到全部的输出。绝大多数数据框中的数据是浮点数。第一列是性别，标记为M（雄性）、F（雌性）和I（不确定的）。鲍鱼的性别在出生时是不确定的，成熟一些之后才能确定。因此对于小的鲍鱼其性别是不确定的。鲍鱼的性别是一个三值的类别变量。类别属性需要特别注意。一些算法只能处理实数值的属性（如支持向量机（support vector machines）、K最近邻、惩罚线性回归，这些将在第4章介绍）。第4章会讨论把类别属性转换成实数值属性的技巧。代码清单2-11还展示了实数值属性按列的统计信息。

代码清单2-11　鲍鱼数据集的读取与分析-abaloneSummary.py

__author__ = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot

target_url = ("http://archive.ics.uci.edu/ml/machine-"
              "learning-databases/abalone/abalone.data")
#read abalone data
abalone = pd.read_csv(target_url,header=None, prefix="V")
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',
                   'Whole weight','Shucked weight', 'Viscera weight',
                   'Shell weight', 'Rings']


print(abalone.head())
print(abalone.tail())

#print summary of data frame
summary = abalone.describe()
print(summary)

#box plot the real-valued attributes
#convert to array for plot routine
array = abalone.iloc[:,1:9].values
boxplot(array)
plot.xlabel("Attribute Index")
plot.ylabel(("Quartile Ranges"))
show()

#the last column (rings) is out of scale with the rest
# - remove and replot
array2 = abalone.iloc[:,1:8].values
boxplot(array2)
plot.xlabel("Attribute Index")
plot.ylabel(("Quartile Ranges"))
show()

#removing is okay but renormalizing the variables generalizes better.
#renormalize columns to zero mean and unit standard deviation
#this is a common normalization and desirable for other operations
# (like k-means clustering or k-nearest neighbors
abaloneNormalized = abalone.iloc[:,1:9]

for i in range(8):
    mean = summary.iloc[1, i]
    sd = summary.iloc[2, i]

abaloneNormalized.iloc[:,i:(i + 1)] = (
                    abaloneNormalized.iloc[:,i:(i + 1)] - mean) / sd


array3 = abaloneNormalized.values
boxplot(array3)
plot.xlabel("Attribute Index")
plot.ylabel(("Quartile Ranges - Normalized "))
show()

Printed Output: (partial)
  Sex Length Diameter Height Whole wt Shucked wt Viscera wt
0   M  0.455    0.365  0.095   0.5140     0.2245     0.1010
1   M  0.350    0.265  0.090   0.2255     0.0995     0.0485
2   F  0.530    0.420  0.135   0.6770     0.2565     0.1415
3   M  0.440    0.365  0.125   0.5160     0.2155     0.1140
4   I  0.330    0.255  0.080   0.2050     0.0895     0.0395

   Shell weight Rings
0         0.150    15
1         0.070     7
2         0.210     9
3         0.155    10
4         0.055     7
     Sex Length Diameter Height Whole weight Shucked weight
4172   F  0.565    0.450  0.165       0.8870         0.3700
4173   M  0.590    0.440  0.135       0.9660         0.4390
4174   M  0.600    0.475  0.205       1.1760         0.5255
4175   F  0.625    0.485  0.150       1.0945         0.5310
4176   M  0.710    0.555  0.195       1.9485         0.9455

     Viscera weight Shell weight Rings
4172         0.2390       0.2490    11
4173         0.2145       0.2605    10
4174         0.2875       0.3080     9
4175         0.2610       0.2960    10
4176         0.3765       0.4950    12
           Length    Diameter      Height    Whole wt  Shucked wt
count 4177.000000 4177.000000 4177.000000 4177.000000 4177.000000
mean     0.523992    0.407881    0.139516    0.828742    0.359367
std      0.120093    0.099240    0.041827    0.490389    0.221963
min      0.075000    0.055000    0.000000    0.002000    0.001000
25%      0.450000    0.350000    0.115000    0.441500    0.186000
50%      0.545000    0.425000    0.140000    0.799500    0.336000
75%      0.615000    0.480000    0.165000    1.153000    0.502000
max      0.815000    0.650000    1.130000    2.825500    1.488000

       Viscera weight Shell weight       Rings
count     4177.000000  4177.000000  4177.000000
mean         0.180594     0.238831     9.933684
std          0.109614     0.139203     3.224169
min          0.000500     0.001500     1.000000
25%          0.093500     0.130000     8.000000
50%          0.171000     0.234000     9.000000
75%          0.253000     0.329000    11.000000
max          0.760000     1.005000    29.000000```
不仅可以列出统计信息，还可以像代码清单2-11那样产生每个实数值属性（列）的箱线图（box plots）。第一个箱线图如图2-9所示。箱线图又叫作盒须图（box and whisker plots）、盒式图、盒状图。这些图显示了一个小长方形，有一个红线穿过它。红线代表此列数据的中位数（第50百分位数），长方形的顶和底分别表示第25百分位数和第75百分位数（或者第一四分位数、第三四分位数）。可以比较打印出来的统计信息和箱线图中的线段来证实这一点。在盒子的上方和下方有小的水平线，叫作盒须（whisker）。它们分别据盒子的上边和下边是四分位间距的1.4倍，四分位间距就是第75百分位数和第25百分位数之间的距离，也就是从盒子的顶边到盒子底边的距离。也就是说盒子上面的盒须到盒子顶边的距离是盒子高度的1.4倍。这个盒须的1.4倍距离是可以调整的，详见箱线图的相关文档。在有些情况下，盒须要比1.4倍距离近，这说明数据的值并没有扩散到原定计算出来的盒须的位置。在这种情况下，盒须被放在最极端的点上。在另外一些情况下，数据扩散到远远超出计算出的盒须的位置（1.4倍盒子高度的距离），这些点被认为是异常点。




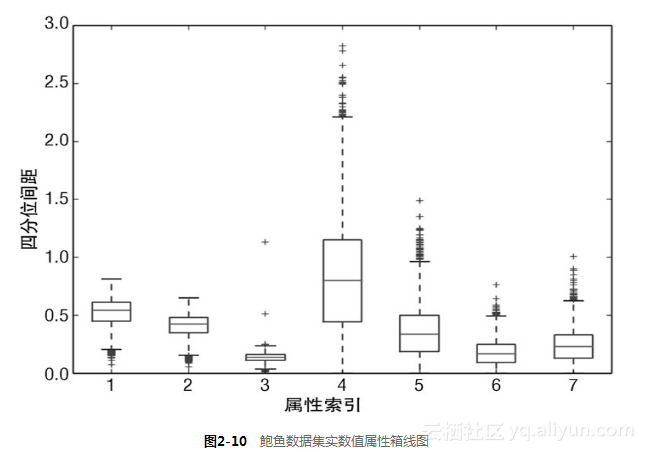
图2-9所示的箱线图是一种比打印出数据更快、更直接的发现异常点的方法，但是最后一个环数属性（最右边的盒子）的取值范围导致其他属性都被“压缩”了（导致很难看清楚）。一种简单的解决方法就是把取值范围最大的那个属性删除。结果如图2-10所示。这个方法并不令人满意，因为没有实现根据取值范围自动缩放（自适应）。




代码清单2-11的最后一部分代码在画箱线图之前将属性值归一化（normalization）。此处的归一化指确定每列数据的中心，然后对数值进行缩放，使属性1的一个单位值与属性2的一个单位值相同。在数据科学中有相当数量的算法需要这种归一化。例如，K-means 聚类方法是根据行数据之间的向量距离来进行聚类的。距离是对应坐标上的点相减然后取平方和。单位不同，算出来的距离也会不同。到一个杂货店的距离以英里为单位是1英里，以英尺为单位就是5 280英尺。代码清单2-11中的归一化是把属性数值都转换为均值为0、标准差为1的分布。这是最通用的归一化。归一化计算用到了函数summary()的结果。归一化后的效果如图2-11所示。




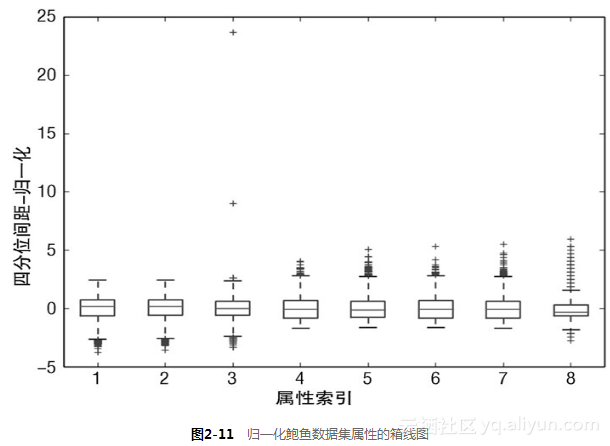注意归一化到标准差1.0并不意味着所有的数据都在−1.0和+1.0之间。盒子的顶边和底边多少都会在−1.0和+1.0附近，但是还有很多数据在这个边界外。

####2.4.1　回归问题的平行坐标图：鲍鱼问题的变量关系可视化
下一步是看属性之间、属性与标签之间的关系。对于“岩石vs.水雷”数据集，加颜色的平行坐标图以图形化方式展示了这两种关系。针对鲍鱼问题，上述方法需要做些修正。岩石vs.水雷是分类问题。平行坐标图对于此类问题，折线代表了一行数据，折线的颜色表明了其所属的类别。这有利于可视化属性和所属类别之间的关系。鲍鱼问题是一个回归问题，应该用不同的颜色来对应标签值的高低。也就是实现由标签的实数值到颜色值的映射，需要将标签的实数值压缩到[0.0,1.0]区间。代码清单2-12由函数summary()获得最大、最小值实现这种转换。结果如图2-12所示。

代码清单2-12　鲍鱼数据的平行坐标图-abalonParallelPlot.py

author = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot
from math import exp

target_url = ("http://archive.ics.uci.edu/ml/machine-"

          "learning-databases/abalone/abalone.data")

read abalone data

abalone = pd.read_csv(target_url,header=None, prefix="V")
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',

               'Whole Wt', 'Shucked Wt',
               'Viscera Wt', 'Shell Wt', 'Rings']

get summary to use for scaling

summary = abalone.describe()
minRings = summary.iloc[3,7]
maxRings = summary.iloc[7,7]
nrows = len(abalone.index)

for i in range(nrows):

#plot rows of data as if they were series data
dataRow = abalone.iloc[i,1:8]
labelColor = (abalone.iloc[i,8] - minRings) / (maxRings - minRings)
dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)

plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()

renormalize using mean and standard variation, then compress

with logit function

meanRings = summary.iloc[1,7]
sdRings = summary.iloc[2,7]

for i in range(nrows):

#plot rows of data as if they were series data
dataRow = abalone.iloc[i,1:8]
normTarget = (abalone.iloc[i,8] - meanRings)/sdRings
labelColor = 1.0/(1.0 + exp(-normTarget))
dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)

plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()`
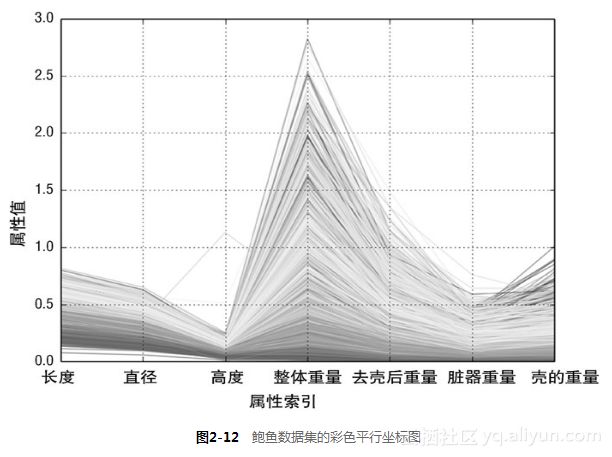
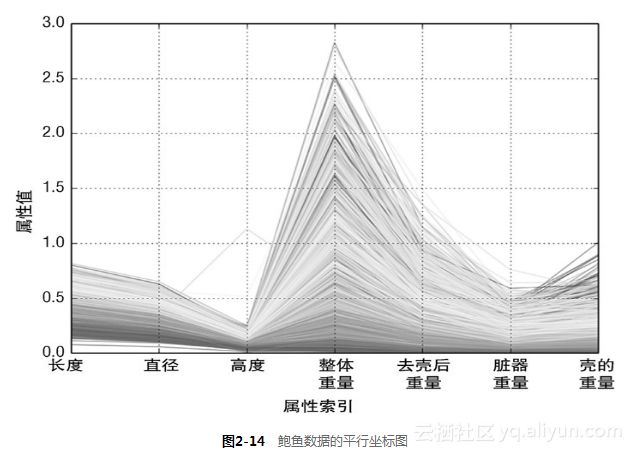
图2-12的平行坐标图为鲍鱼年龄（壳的环数）和用于预测年龄的属性之间的关系。折线使用的颜色标尺从深红棕色、黄色、浅蓝色一直到深蓝色。图2-11的箱线图显示整个数据集的最大值和最小值分布十分广泛。图2-12有压缩的效果，导致绝大多数的数据都分布在颜色标尺的中间部分。尽管如此，图2-12还是能够显示每个属性和目标环数的相关性。在属性值相近的地方，折线的颜色也比较接近，则会集中在一起。这些相关性都暗示可以构建相当准确的预测模型。相对于那些体现了良好相关性的属性和目标环数，有些微弱的蓝色折线与深橘色的区域混合在一起，说明有些实例可能很难正确预测。

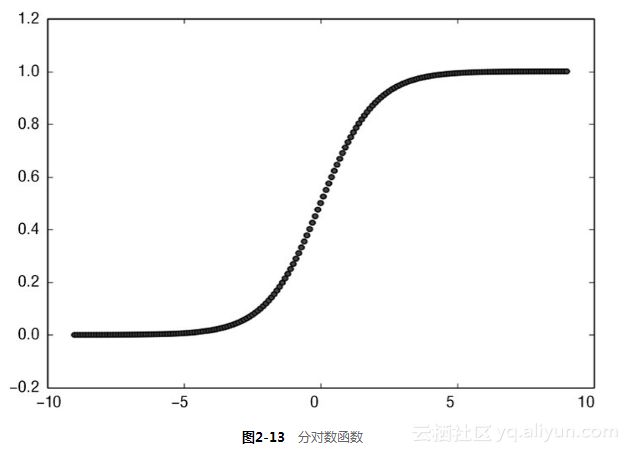
改变颜色映射关系可以从不同的层面来可视化属性与目标之间的关系。代码清单2-11的最后一部分用到了箱线图中用过的归一化。此归一化不是让所有的值都落到0和1之间。首先让取负值的数据与取正值的数据基本上一样多。代码清单2-11中使用分对数变换（logit transform）实现数值到（0,1）的映射。分对数变换如公式2-5所示，分对数函数如图2-13所示。

如图2-13所示，分对数函数将很大的负数映射成０（接近），很大的正数映射成1（接近），０映射成0.5。在第4章还会看到分对数函数，在将线性函数与概率联系起来它起到了关键的作用。

图2-14为归一化之后的结果。转换后可以更充分地利用颜色标尺中的各种颜色。注意到针对整体重量和去壳后的重量这两个属性，有些深蓝的线（对应具有大环数的品种）混入了浅蓝线的区域，甚至是黄色、亮红的区域。这意味着，当鲍鱼的年龄较大时，仅仅这些属性不足以准确地预测出鲍鱼的年龄（环数）。好在其他属性（如直径、壳的重量）可以很好地把深蓝线区分出来。这些观察都有助于分析预测错误的原因。

2.4.2　回归问题如何使用关联热图—鲍鱼问题的属性对关系的可视化

最后一步是看不同属性之间的相关性和属性与目标之间的相关性。代码清单2-13为针对鲍鱼数据产生关联热图和关系矩阵的代码。遵循的方法与“岩石vs.水雷”数据集相应章节里的方法一样，只有一个重要差异：因为鲍鱼问题是进行实数值预测，所以在计算关系矩阵时可以包括目标值。

代码清单2-13　鲍鱼数据的相关性计算-abaloneCorrHeat.py

__author__ = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot

target_url = ("http://archive.ics.uci.edu/ml/machine-"
              "learning-databases/abalone/abalone.data")
#read abalone data
abalone = pd.read_csv(target_url,header=None, prefix="V")
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',
                   'Whole weight', 'Shucked weight',
                   'Viscera weight', 'Shell weight', 'Rings']

#calculate correlation matrix
corMat = DataFrame(abalone.iloc[:,1:9].corr())
#print correlation matrix
print(corMat)

#visualize correlations using heatmap
plot.pcolor(corMat)
plot.show()

                 Length Diameter   Height Whole Wt  Shucked Wt
Length         1.000000 0.986812 0.827554  0.925261   0.897914
Diameter       0.986812 1.000000 0.833684  0.925452   0.893162
Height         0.827554 0.833684 1.000000  0.819221   0.774972
Whole weight   0.925261 0.925452 0.819221  1.000000   0.969405
Shucked weight 0.897914 0.893162 0.774972  0.969405   1.000000
Viscera weight 0.903018 0.899724 0.798319  0.966375   0.931961
Shell weight   0.897706 0.905330 0.817338  0.955355   0.882617
Rings          0.556720 0.574660 0.557467  0.540390   0.420884

               Viscera weight Shell weight    Rings
Length               0.903018     0.897706 0.556720
Diameter             0.899724     0.905330 0.574660
Height               0.798319     0.817338 0.557467
Whole weight         0.966375     0.955355 0.540390
Shucked weight       0.931961     0.882617 0.420884
Viscera weight       1.000000     0.907656 0.503819
Shell weight         0.907656     1.000000 0.627574
Rings                0.503819     0.627574 1.000000```
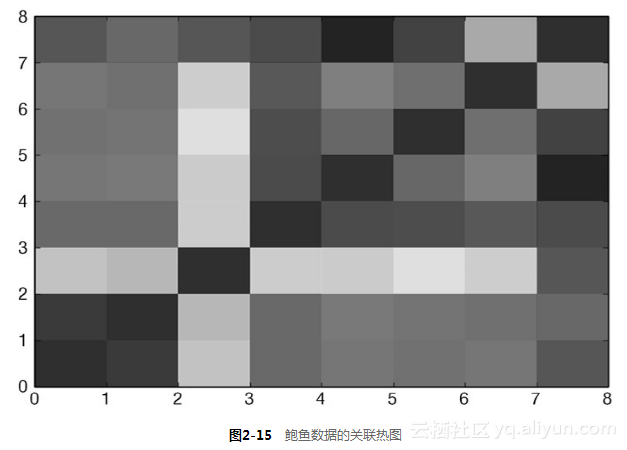
图2-15为关联热图。在图2-15中，红色代表强相关，蓝色代表弱相关。目标（壳上环数）是最后一项，即关联热图的第一行和最右列。蓝色说明这些属性与目标弱相关。浅蓝对应目标与壳的重量的相关性。这个结果与在平行坐标图看到的一致。如图2-15所示，在偏离对角线的单元内，红棕色的值代表这些属性相互高度相关。这多少与平行坐标图的结论有些矛盾，因为在平行坐标图中，目标与属性的一致性是相当强的。代码清单2-13展示了具体的关联值。