使用线性回归，岭回归，Lasso回归预测鲍鱼年龄

实验目的
掌握数据预处理方法
掌握线性回归预测基本原理与实现。
实验问题背景
鲍鱼的年龄可以通过鲍鱼壳的“环数”来判断，但是获取这个“环数”是十分耗时的，需要锯开壳，然后在显微镜下观察得到。
可以通过鲍鱼的其他特征比如性别、长度、直径、高度、整体重量、去壳后重量、脏器重量、壳的重量等，通过机器学习的方法来预测其环数，从而得到年龄，具有很大的应用价值。
实验问题描述
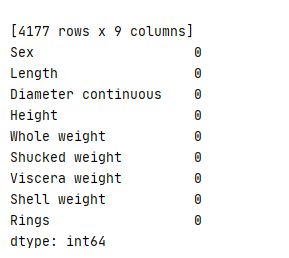
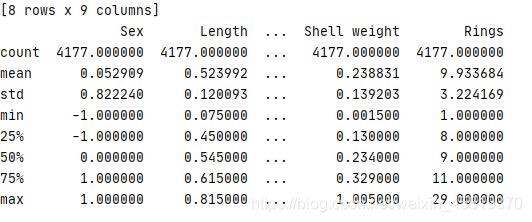
现有一份鲍鱼的数据集abalone.csv，该数据集有4177个数据样本，每个样本有9个特征，具体信息如下：
属性 数据类型 单位 内容描述
性别（Sex） 标称 M, F,I(infant)
长度（Length） 连续 毫米
直径（Diameter） 连续 毫米
高度（Height） 连续 毫米
整体重量（Whole weight） 连续 克
去壳后重量（Shucked weight） 连续 克
脏器重量（Viscera weight） 连续 克
壳的重量（Shell weight） 连续 克
环数（Rings） 连续
实验内容：
1.数据预处理：
(1)标称数据的连续化：利用函数将性别Sex列中的‘F’，’M’用‘0’，‘1’等数字表示
程序：

结果：Sex标称已经实现连续化

(2)发现数据中的NaN，并用中位值填补
程序实现
发现NaN

中位值填补

结果：数据中空值已被填补

(3)处理极端值，并导出到新的csv文件中
1.为了观察有没有明显错误的值，采用了画图的方法来观测极端值
箱型图：

发现散点图更为直观。

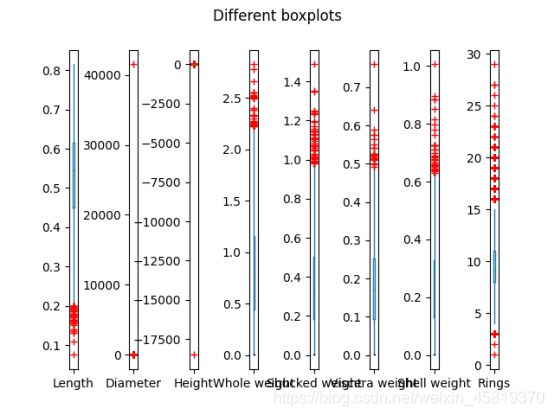
1.在第二三列中发现极端值，而且极端值的绝对值远远大于普通数据的绝对值，因此利用其特性将其替换
想法：去掉绝对值大于平均值四倍的数据，并用该列的中位数填补
（ 选择临界点为平均值四倍的原因：为了适应每列的情况不同，最好采用每列的特征值，而不是固定数，平均值是反映数据集中趋势的一项重要指标，而且还要给数据一些灵活度，因此选择平均值的四倍作为临界点。
选择中位数的原因：极端值会影响平均值，因此用中位数来替代。
）

结果：发现max，min恢复正常，原极端值被删除

2.将数据集按照3:1分为训练集和验证集
因为目的是通过鲍鱼其它特征来预测鲍鱼年龄环数，因此用X,Y来将变量因变量分开。
然后引入 sklearn.model_selection 中的train_test_split包，划分训练集和验证集。
程序：

3.调用第三方软件包（比如Sklearn）实现线性回归、岭回归、LASSO回归
①　普通线性回归实现
调用sklearn.linear_model中的LinearRegression，将训练集带入，求出参数，
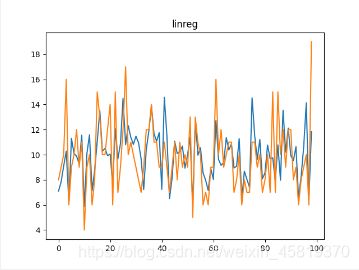
并将测试集带入用来检测，并画出拟合图像。

结果：b = 3.0132231704721466
各列的系数为：
[ 0.08407275 -2.66150222 15.14972465 10.03392069 8.79095617
-19.95672912 -8.20363118 8.61863201]
Score值，即决定系数R^2为：
0.5266091889605017
（决定系数R^2
决定系数（coefficient ofdetermination），有的教材上翻译为判定系数，也称为拟合优度。
决定系数反应了y的波动有多少百分比能被x的波动所描述，即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释。
意义：拟合优度越大，说明x对y的解释程度越高。自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。）
可视化图像：

②　岭回归
由于岭回归受参数alpha的影响较大，所以先画图分析，选取较好的alpha参数。

上图能够看到各个数组的回归系数随参数alpha的变化。可以看到，随着λ的变大，所有回归系数都缩减到0。
横坐标选择：通过观察，选取喇叭口附近的值，此时各系数取值已趋于稳定，通过观察岭迹线大于10次方 各个特征的权重就几乎为0了，而小于10^-2次方 某些特征的权重的变化幅度就会非常大，很容易出问题，所以猜测，在10^-3次方到10的1次方之间取一个alpha值比较合适。
规定大致范围后，选取尚不明显，因此通过枚举的方式作图来更加直观的观察。

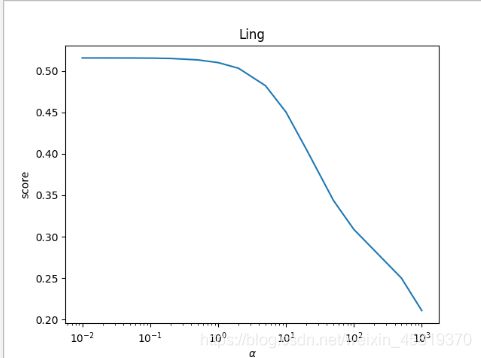
令alpha取各个不同的值，分别带入岭回归求取score，发现alpha在接近10^-2到10这一段score值较为平缓，而后随着alpha的增大，score逐渐变小，这也与上个回归系数图的观察相吻合，因此选取alpha == 1.
然后借助sklearn函数，带入训练测试集，创建岭回归。

结果：
b = 3.272111284388725
各列系数：[ 0.07303543 2.41349521 8.20099343 7.32182758 6.69908352 -17.21552799 -4.83336808 10.46067075]
Score值（R^2)：0.5189765084864537
拟合图像显示：

③　LASSO回归
与岭回归相似的是，lasso也受参数alpha的影响，因此先通过可视化选取适合的alpha值。
首先：

画出lasso的正则化拟合曲线，观察到在alpha变化的过程中，通过观察大于0.1各个特征的权重就已经接近0，小于0.05时，而特征权重变化幅度过大，j极易出问题.因此，初步确定alpha在0.1-0.05这个范围内。
进一步确定：

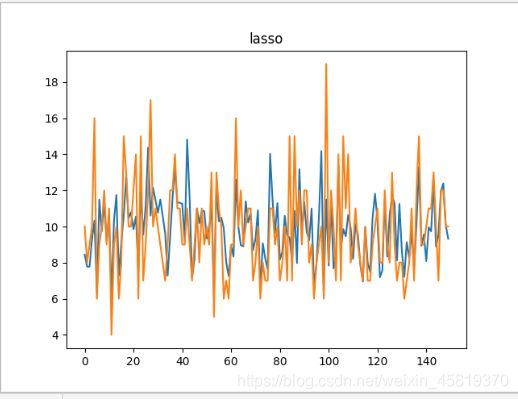
将alpha的多个值带入，求出其score值，通过图像观察，发现随着alpha的增大，score减少，且当alpha的值大于1时，score值几乎接近于0，因此，选取alpha为0.01，并将参数带入，求lasso回归

得出结果：
b = 3.610186708754836
各项系数：[ 0. 0. 9.35199529 9.47261795 0. -8.60890724 0. 17.80445353]
Score值：0.49434794625533063
拟合图像：

4.编程实现线性回归和岭回归算法

1)实现线性回归

根据原理，进行编程：
注意：将X,Y转化为矩阵。

另外，引用了numpy的库，来实现矩阵运算。
输出结果：
得到各项系数：[ 0.10762547 5.0079725 15.42687314 12.4400711 8.21075551
-20.84413583 -9.86107619 6.9365935 ]

实现岭回归

程序实现：

得出结果：
各项系数：[ 0.1007056 8.83355883 11.08854968 9.39323737 5.66562161
-17.8600036 -5.96550196 9.10760764]

发现分析：
分析：1.由于岭回归实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。lasso回归在线性回归的损失函数的基础上加上了L1正则化参数，L1正则项是为了使得那些原先处于零（即|w|≈0）附近的参数w往零移动，使得部分参数为零，从而降低模型的复杂度（模型的复杂度由参数决定），从而防止过拟合，提高模型的泛化能力。也因此，训练集的拟合能力被限制住了.相比普通线性回归模型确实不容易过拟, 但是却有可能出现欠拟。因此，在该已经处理过异常值的数据下，普通的线性回归模型所得到的决定系数要优于牺牲了部分信息降低精度的岭回归与lasso回归。
2.Lasso 的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于0 的回归系数，得到可以解释的模型。所以在lasso回归中可以看到许多为0的回归系数。
代码及数据集下载：
https://github.com/wmj555/-01