图像金字塔

• **学习图像金字塔的原理
• 使用图像金字塔进行一个图像的融合
• 学习的函数有cv2.pyrUp, cv2.pyrDown**

原理

一般情况下,我们要处理是一副具有固定分辨率的图像。但是有些情况下,
我们需要对同一图像的不同分辨率的子图像进行处理。比如,我们要在一幅图
像中査找某个目标,比如脸,我们不知道目标在图像中的尺寸大小。这种情况
下,我们需要创建创建一组图像,这些图像是具有不同分辨率的原始图像。我
们把这组图像叫做图像金字塔(简单来说就是同一图像的不同分辨率的子图集
合)如果我们把最大的图像放在底部,最小的放在顶部,看起来像一座金字
塔,故而得名图像金字塔。
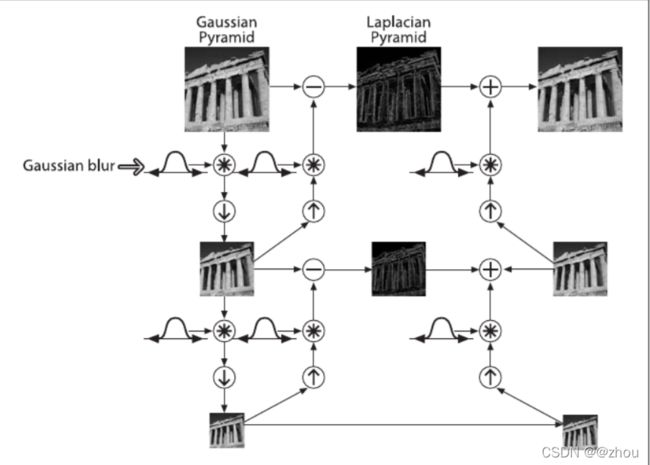
有两类图像金字塔:高斯金字塔和拉普拉斯金字塔。
高斯金字塔的顶部是通过将底部图像中的连续的行和列去除得到的。顶
部图像中的每个像素值等于下一层图像中5个像素的高斯加权平均值。这样
操作一次一个$(M,N)$的图像就变成了一个$(\frac{M}{2},\frac{N}{2})$的图像。所以这幅图像的面积就变为原来图像面积的四分之一。这被称为 Octave。连续进行这样
的操作我们就会得到一个分辨率不断下降的图像金字塔。我们可以使用函数
cv2 pyrDown和cv2 pyrUp构建图像金字塔
函数cv2 pyrDown(从一个高分辨率大尺寸的图像向上构建一个金子塔
尺寸变小,分辨率降低):

img = cv2.imread(path)
img = cv2.pyrDown(img)

例如下图：我们将建立一个三层的金字塔模型，并绘画出图像

如果要观察原图和第三幅图像的分辨率，我们将其所占的空间长度取相等，观察那个图片的清晰度好：

显而易见经过两次的Down操作，图片的分辨率变低，视觉上的效果就是图片变得有点模糊，不如原图来的清晰。

拉普拉斯金字塔可以通过高斯金字塔计算得到，给出下面的公式：
$$L_i=G_i-cv2.pyrUp(G_{i+1})$$
拉普拉斯相对于高斯金字塔，它的作用是将图片的size放大2倍，查阅了相关资料后得知，拉普拉斯金字塔体现的是一种残差，所以拉普拉斯其中的像素很多是0，而且拉普拉斯金字塔不改变图像的分辨率，

图像融合实战

• 读取两幅图片，并对其resize尺寸为2的幂次，不然以后融合的时候不对
• 建立6层的高斯金字塔
• 之后通过上面的公式得到拉普拉斯金字塔
• 之后将两种水果的各层金字塔分别进行拼接，得到新的金字塔
• 对新的金字塔进行重建,最终得到融合后的图像，并且与简单拼接得到的融合图像对比
  
  结果：我们将经过金字塔融合后得到的水果和简单的拼接之后得到的水果同展现在一张图片中，我们发现前者融合后的结果非常的平滑，也看不到明显的缝合痕迹，而后者中它的缝合痕迹是相对明显。
  

import cv2
import matplotlib.pyplot as plt
import numpy as np

# cv2.pyrUp cv2.pyrDown
img = cv2.imread('original.JPG')
image_L = [img]
for i in range(2):
    image_L.append(cv2.pyrDown(image_L[i]))

(leng, wid, depth) = img.shape
new = np.zeros((leng+image_L[1].shape[0], wid, depth), dtype=img.dtype)
new[:leng, :wid] = image_L[0]
new[leng:, :image_L[1].shape[1]] = image_L[1]
new[leng:(leng+image_L[2].shape[0]), image_L[1].shape[1]:(image_L[1].shape[1]+image_L[2].shape[1])] = image_L[2]
plt.imshow(new)
plt.axis('off')
plt.show()

# plot 不同分辨率下的图片清晰度
plt.subplot(121)
plt.imshow(image_L[0])
plt.axis('off')
plt.title('Original image')
plt.subplot(122)
plt.imshow(image_L[-1])
plt.axis('off')
plt.title('3 pyrDown')
plt.show()

apple = cv2.imread('Apple.JPG')
orange = cv2.imread('orange.JPG')
apple = cv2.resize(apple, (512, 512))
orange = cv2.resize(orange, (512, 512))
plt.subplot(221)
plt.imshow(apple, cmap='hsv')
plt.axis('off')
plt.title('original Apple')
plt.subplot(222)
plt.imshow(orange, cmap='hsv')
plt.title('original Original')
plt.axis('off')



gao_apple = [apple]
gao_orange = [orange]
for i in range(5):
    img = cv2.pyrDown(gao_apple[i])
    print(img.shape)
    gao_apple.append(img)

for i in range(5):
    img = cv2.pyrDown(gao_orange[i])
    print(img.shape)
    gao_orange.append(img)


la_apple = [gao_apple[-1]]
la_orange = [gao_orange[-1]]
for i in range(5, 0, -1):
    img1 = cv2.pyrUp(gao_apple[i])
    #print(img1.shape)
    img = cv2.subtract(gao_apple[i-1], img1)
    #print(img.shape)
    la_apple.append(img)

for i in range(5, 0, -1):
    img1 = cv2.pyrUp(gao_orange[i])
    #print(img1.shape)
    img = cv2.subtract(gao_orange[i-1], img1)
    #print(img.shape)
    la_orange.append(img)

for i in range(5):
    w, h, d = la_apple[i].shape
    la_apple[i][:, int(h/2):, :] = la_orange[i][:, int(h/2):, :]

blend_img = la_apple[0]
for i in range(1, 6):
    img = cv2.pyrUp(blend_img)
    blend_img = cv2.add(la_apple[i], img)

plt.subplot(223)
plt.imshow(blend_img, cmap='hsv')
plt.title('Blend image')
plt.axis('off')
plt.subplot(224)
w, h, d = apple.shape
apple[:, int(h/2):] = orange[:, int(h/2):]
plt.imshow(apple, cmap='hsv')
plt.title('Easy hstack')
plt.axis('off')

plt.show()

在编写代码的时候出现的问题

• 在我编写图融合的代码中出现的问题就是如果图片的初始尺寸不是2的幂次，那么在后来的拉普拉斯操作中将会出现报错的情况，比如$G_i$的尺寸为（25,25），那么$G_{i+1}$的尺寸为（12,12），经过Up之后尺寸变为（24,24）此时我们进行减法的时候将会报错，所以我们读取照片之后，需要进行这一步的预处理，将图片resize为2的幂次$(2^m,2^n)，m,n为整数$。
• 另外的一点就是我们对图像进行加减法是不要使用简单的+、-符号，我们应该使用subtract和add函数，opencv里面的这两个内置函数可以帮助我们计算图片的加减法而且还可以对图片，起到平滑的作用。详细的解释可以参考这篇博客里面有对这两种加减法的试验和比较：https://blog.csdn.net/LaoYuanPython/article/details/109020778