NeRF学习笔记(含公式、图解和过程)
NeRF学习笔记
引言
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis作为2020年ECCV的一篇论文,在用深度学习完成图形学中非常重要的渲染任务上作出了很重要的贡献。此学习笔记主要分为以下几个部分:
1.问题的提出
2.NeRF工作的Pipeline
3.NeRF详细工作的解析
①Neural Radiance Field Scene Representation
②Volume Rendering with Radiance Fields
③Positional encoding
④Hierarchical volume sampling
⑤Implementation details
4.参考文献
1.问题的提出
视角合成方法通常使用一个中间3D场景表征作为中介来生成高质量的虚拟视角,如何对这个中间3D场景进行表征,分为了“显示表示“和”隐式表示“,然后再对这个中间3D场景进行渲染,生成照片级的视角。
“显示表示”3D场景包括Mesh,Point Cloud,Voxel,Volume等,它能够对场景进行显式建模,但是因为其是离散表示的,导致了不够精细化会造成重叠等伪影,更重要的是,它存储的三维场景表达信息数据量极大,对内存的消耗限制了高分辨率场景的应用。
”隐式表示“3D场景通常用一个函数来描述场景几何,可以理解为将复杂的三维场景表达信息存储在函数的参数中。因为往往是学习一种3D场景的描述函数,因此在表达大分辨率场景的时候它的参数量相对于“显示表示”是较少的,并且”隐式表示“函数是种连续化的表达,对于场景的表达会更为精细。
NeRF做到了利用”隐式表示“实现了照片级的视角合成效果,它选择了Volume作为中间3D场景表征,然后再通过Volume rendering实现了特定视角照片合成效果。可以说NeRF实现了从离散的照片集中学习出了一种隐式的Volume表达,然后在某个特定视角,利用该隐式Volume表达和体渲染得到该视角下的照片。
2.NeRF工作的Pipeline
简单的来说,NeRF工作的过程可以分成两部分:三维重建和渲染。
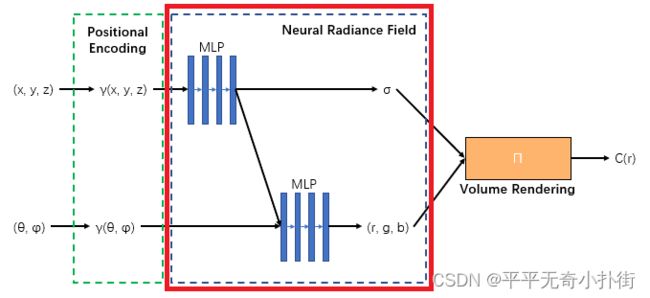
Ⅰ、三维重建部分本质上是一个2D到3D的建模过程,利用3D点的位置(x,y,z)及方位视角(θ,φ)作为输入,通过多层感知机(MLP)建模该点对应的颜色color(c)及体素密度volume density(σ),形成了3D场景的”隐式表示“。(详情看①Neural Radiance Field Scene Representation部分,即下图的红框部分)
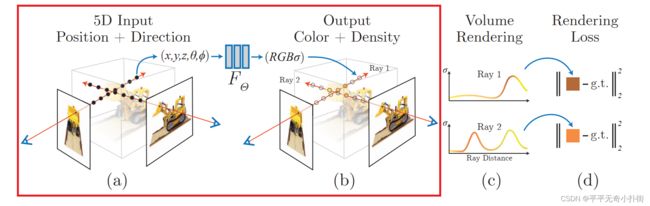
Ⅱ、渲染部分本质上是一个3D到2D的建模过程,渲染部分利用重建部分得到的3D点的颜色及不透明度沿着光线进行整合得到最终的2D图像像素值。(详情看②Volume Rendering with Radiance Fields部分,即下图的红框部分)
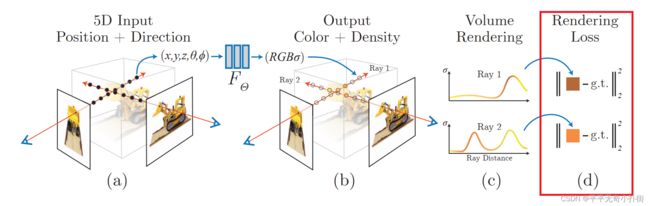
Ⅲ、在训练的时候,利用渲染部分得到的2D图像,通过与Ground Truth做L2损失函数(L2 Loss)进行网络优化。(即下图的红框部分)
3.NeRF详细工作的解析
①Neural Radiance Field Scene Representation
该部分的输入是三维位置(x,y,z)和二维方位视角(θ,φ),输出是颜色c=(r,g,b)和体素密度σ,即利用一个MLP网络近似地表示这种映射F:(x,d) -> (c,σ),这个映射F就是一种3D场景的”隐式表示“。
该MLP网络先使用8个全连接层处理三维位置(x,y,z),输出体素密度σ和256维特征向量(因此体素密度σ仅是关于三维位置(x,y,z)的函数);然后将上面得到的256维特征向量与二维方位视角(θ,φ)concat,接着用4个全连接层处理,输出颜色c=(r,g,b)。(当然,这里预处理需要使用高频位置编码,详细信息看③Positional encoding部分)
②Volume Rendering with Radiance Fields
该部分使用经典体渲染(Volume Rendering)的原理渲染通过场景的任何光线的颜色,即下面这条式子:
C ( r ) = ∫ t n t f T ( t ) σ ( r ( t ) ) c ( r ( t ) , d ) d t , w h e r e T ( t ) = ∫ t n t σ ( r ( s ) ) d s C(r)=\int_{t_n}^{t_f}T(t)σ(r(t))c(r(t), d)dt,whereT(t)=\int_{t_n}^{t}σ(r(s))ds C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt,whereT(t)=∫tntσ(r(s))ds
其中函数T(t)表示射线从tn到t沿射线累积透射率,即射线从tn到t不碰到任何粒子的概率。从①中建模的Neural Radiance Field中绘制视图,需要估计通过所需虚拟相机的每个像素跟踪的相机光线的积分C®,然而①中建模后选取了Volumn作为3D中间表示,势必会使用到离散求积法对这个连续积分进行数值估计,这会极大地限制表示的分辨率,因此可通过分层抽样方法(详细信息看④Hierarchical volume sampling部分)的方法,使得即使使用离散的样本估计积分,但是能够较好地表示一个连续的场景(类似重要性采样,对整个积分域进行非均匀离散化,较能还原原本的积分分布)。
其中离散化式子为:
C ^ ( r ) = ∑ i = 1 N T i ( 1 − e x p ( − σ i δ i ) ) c i , w h e r e T i = e x p ( − ∑ j = 1 i − 1 σ j δ j ) \hat C(r)=\sum_{i=1}^NT_i(1-exp(-\sigma_i\delta_i))c_i,whereT_i=exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j) C^(r)=i=1∑NTi(1−exp(−σiδi))ci,whereTi=exp(−j=1∑i−1σjδj)
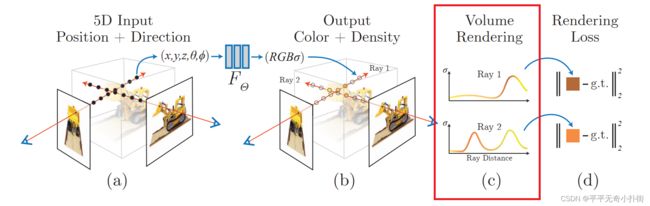
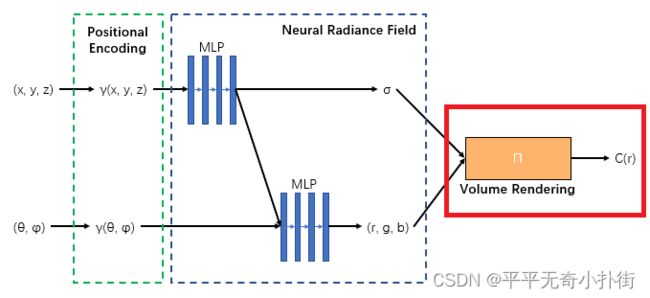
该部分即下图红框部分:
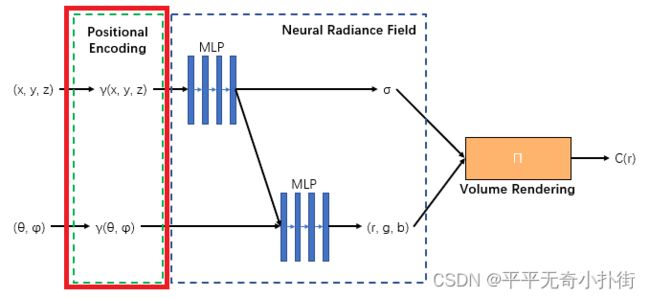
③Positional encoding
该部分中指出尽管神经网络是通用的函数近似器,但是他们发现,让①中的MLP网络(F:(x,d) -> (c,σ))直接操作 (x,y,z,θ,φ)输入会导致渲染在表示颜色和几何形状方面的高频变化方面表现不佳,表明深度网络偏向于学习低频函数。因此在将(x,y,z,θ,φ)输入传递给网络之前,使用高频函数将输入映射到更高维度的空间,可以更好地拟合包含高频变化的数据。该高频编码函数为:
γ ( p ) = ( s i n ( 2 0 π p ) , c o s ( 2 0 π p ) , . . . , s i n ( 2 L − 1 π p ) , c o s ( 2 L − 1 π p ) ) \gamma(p)=(sin(2^0\pi p),cos(2^0\pi p),...,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p)) γ(p)=(sin(20πp),cos(20πp),...,sin(2L−1πp),cos(2L−1πp))
这个高频编码函数有点类似傅里叶级数的方式,其中p就是(x,y,z,θ,φ)输入,并且输入均归一化于[-1,1],在实验中针对于(x,y,z)输入取L=10,针对于(θ,φ)输入取L=4,即:
γ ( ( x , y , z ) ) = ( s i n ( 2 0 π ( x , y , z ) ) , c o s ( 2 0 π ( x , y , z ) ) , . . . , s i n ( 2 9 π ( x , y , z ) ) , c o s ( 2 9 π ( x , y , z ) ) ) \gamma((x,y,z))=(sin(2^0\pi (x,y,z)),cos(2^0\pi (x,y,z)),...,sin(2^{9}\pi (x,y,z)),cos(2^{9}\pi (x,y,z))) γ((x,y,z))=(sin(20π(x,y,z)),cos(20π(x,y,z)),...,sin(29π(x,y,z)),cos(29π(x,y,z)))
γ ( ( θ , φ ) ) = ( s i n ( 2 0 π θ , φ ) , c o s ( 2 0 π θ , φ ) , . . . , s i n ( 2 3 π θ , φ ) , c o s ( 2 3 π θ , φ ) ) \gamma((θ,φ))=(sin(2^0\pi θ,φ),cos(2^0\pi θ,φ),...,sin(2^{3}\pi θ,φ),cos(2^{3}\pi θ,φ)) γ((θ,φ))=(sin(20πθ,φ),cos(20πθ,φ),...,sin(23πθ,φ),cos(23πθ,φ))
④Hierarchical volume sampling
该部分指出在Volume Rendering中是在每条相机光线上的N个查询点密集地评估神经辐射场网络,这是低效的(仍然重复采样与渲染图像无关的自由空间和遮挡区域),于是提出一种分层体积采样的做法,同时优化一个“粗糙”的网络和一个“精细”的网络。
做法是:首先使用分层抽样对第一组Nc位置进行采样,并在这些位置评估“粗糙”网络。给出这个“粗糙”网络的输出,然后我们对每条射线上的点进行更明智的采样,即利用反变换采样从这个分布中采样第二组Nf位置,然后将Nc+Nf采样得到的数据输入“精细”网络,并计算最终渲染的光线颜色C®。
核心操作即先通过第一次采样把大概的分布采出来,然后第二次采样利用反变换采样(用的是概率论中的拒绝采样),对第一次采到的大概的分布再采一次,达到了重要性采样的目的。
⑤Implementation details
Ⅰ、关于Loss
Loss是④中提到的“粗糙”网络和“精细”网络渲染结果和真实像素颜色之间的总平方误差。
L o s s = ∑ r ∈ R [ ∣ ∣ C ^ c ( t ) − C ( r ) ∣ ∣ 2 2 + ∣ ∣ C ^ f ( t ) − C ( r ) ∣ ∣ 2 2 ] Loss=\sum_{r\in R}[||\hat C_c(t)-C(r)||_2^2+||\hat C_f(t)-C(r)||_2^2] Loss=r∈R∑[∣∣C^c(t)−C(r)∣∣22+∣∣C^f(t)−C(r)∣∣22]
其中Cc®为“粗糙”网络输出,Cf®为“精细”网络的输出。
Ⅱ、关于一些超参数
Batchsize为4096条射线(Ray)。
每条射线在粗体积中Nc=64坐标下采样,在细体积中Nf=128额外坐标下采样。
使用Adam优化器,学习速率从5e-4,并在优化过程中指数衰减到5e-5。
优化一个场景通常需要10 - 30万次迭代,集中在一个NVIDIA V100 GPU上(大约1-2天)。
4.参考文献
[1] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
[2] NeRF的数学推导
[3] NeRF及其发展
[4] 图形学新高潮? NeRF 笔记