Spatial-Temporal Fusion Graph Neural Networks 阅读笔记
参考资料:
论文笔记:https://zhuanlan.zhihu.com/p/342483943
DTW算法:https://blog.csdn.net/zouxy09/article/details/9140207
Spatial-Temporal Fusion Graph Neural Networks 阅读笔记
1、Abstract
当前模型存在问题:
-
通过含不完全的邻接连接的空间图结构表示能力有限,限制了这些模型有效地学习时空相关性。
-
通常使用单独的模块来实现空间和时间相关性,或者只使用独立的组件来捕获局部或全局的异质依赖关系的方法在处理复杂的时空数据时效果不好。
本文提出了一种新的网络STFGNN
- 使用数据驱动的方法生成temporal graph,用以弥补时空图不能反映的关系。
- 一种新的时间图和空间图的融合方法
- 将图融合模块和门控卷积融合到统一的层中
2、Introduction
当前一些模型存在以下不足:
1.缺乏一个有效的信息图结构
当前大部分模型通过空间邻接矩阵来构建图这种做法忽略了具有相同时间模式的节点关系(比如在高峰期,写字楼附近的路段会在同一时期遭遇交通拥堵的情况)
以往的一些改进
- Mask matrix
- self-adaptive matrix
以上两种方法都缺乏对复杂时空相关性的表征能力。
- Temporal self-attention module :可以提取动态的时空相关性,但是在长时间范围的预测中由于时空数据的动态变化和噪音,该模块面临过拟合问题,且对于自回归模型而言误差积累难以避免
2.当前一些模型难以捕捉局部和全局之间的依赖关系
- 基于RNN/LSTM的模型:费时,且在捕捉长期依赖时容易遭受梯度消失和梯度爆炸问题
- transformer之类的序列方法:计算复杂度高
- 基于CNN的方法:扩张率变大时容易丢失局部信息
主要贡献:
-
通过数据驱动的方法构建了一个新的图结构,并且提出了一种新的时空融合图模块来同步捕获时空相关性
-
提出了一个有效的框架来同时捕捉局部和全局相关性,通过将门控扩张的CNN模块与时空融合图模块并行组装。
3.Related Works
**Similarity of Temporal Sequences:**时间序列相似度的算法可以分为三类:(1)基于时间步的(2)基于形状的(3)基于变化的
本文使用的时基于形状的DYW算法,DTW算法主要思路
1.计算两个序列各个点之间的距离矩阵。
给定两个时间序列: X = ( x 1 , x 2 , ⋯ , x n ) , Y = ( y 1 , y 2 , ⋯ , y m ) X=(x_{1}, x_{2}, \cdots, x_{n}),Y=(y_{1}, y_{2}, \cdots, y_{m}) X=(x1,x2,⋯,xn),Y=(y1,y2,⋯,ym) ,计算量两个时间序列之间的距离矩阵 M n × m M_{n\times m} Mn×m
2.寻找一条从矩阵左上角到右下角的最短距离
DWT在寻找该路径时给出了三个限制:
1)边界条件:w1=(1, 1)和wk=(m, n)。即所选的路径必定是从左下角出发,在右上角结束。
2)连续性:如果wk-1= (i’, j’),那么的下一个点wk=(i, j)需要满足 (i-i’) <=1和 (j-j’) <=1。也就是不可能跨过某个点去匹配,只能和自己相邻的点对齐。
3)单调性:如果wk-1= (i’, j’),那么对于路径的下一个点wk=(i, j)需要满足0<=(i-i’)和0<= (j-j’)。这限制W上面的点必须是随着时间单调进行的。也就是不能回退。
显然问题可以由动态规划求出最短路径,定义如下:
M c ( i , j ) = M i , j + min ( M c ( i , j − 1 ) , M c ( i − 1 , j ) , M c ( i , j ) ) M_{c}(i, j)=M_{i, j}+\min \left(M_{c}(i, j-1), M_{c}(i-1, j), M_{c}(i, j)\right) Mc(i,j)=Mi,j+min(Mc(i,j−1),Mc(i−1,j),Mc(i,j))
由于DWT算法的时间复杂度是 O ( n 2 ) \mathcal{O}\left(n^{2}\right) O(n2),由于在很多现实生活时间序列都很长所以难以应用带现实一些问题中,所以作者在这边对他加了限制:
ω k = ( i , j ) , ∣ i − j ∣ ≤ T \omega_{k}=(i, j), \quad|i-j| \leq T ωk=(i,j),∣i−j∣≤T
将时间复杂度由 O ( n 2 ) \mathcal{O}\left(n^{2}\right) O(n2)降低到 O ( T n ) \mathcal{O}(T n) O(Tn)。
4.Spatial-Temporal Fusion Graph Neural Networks
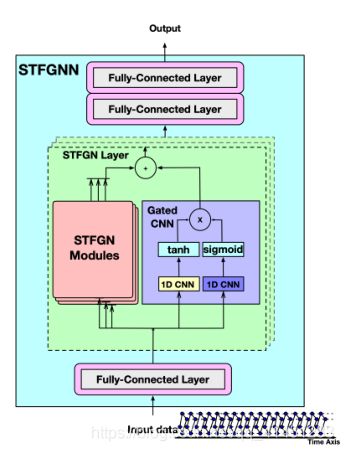
Spatial-Temporal Fusion Graph Neural Network由三部分组成(1)输入层(2)堆叠的STFGN(3)输出层
网络总图如下
1.Spatial-Temporal Fusion Graph Construction
生成时态图是为了获得比空间图更精确的依赖关系和真实关系的图结构,这可以使深度学习模型变得轻量级,因为该融合图已经具有每个节点与其(1)空间邻居(2)具有相似时间模式的节点(3)沿着时间轴拥有以前或以后的情况。时空图生成算法如下:

算法大概步骤:首先利用TDL算法计算出每个节点之间的时空序列的差异性,取出最小的k个标记为具有相同时间模式的节点,这样就得到了时间图ATG。最终的时空图是由三种图合成的分别是(1)空间图ASG,时间图ATG和时间连接图ATC。其中ATC表示同一节点在相近时间步长的连接。是一个对称轴为1,其余为0的 N × N N\times N N×N矩阵,三种图的融合见下图。最终生成的时空融合图为 A S T F G ∈ R K N × K N A_{STFG}\in\mathbb{R}^{KN\times KN} ASTFG∈RKN×KN这边的K我认为是作者将原始输入切割 X = [ X G ( t ) , ⋯ , X G ( t + T ) ] ∈ R T × N × d × C X=\left[X_{\mathcal{G}}^{(t)}, \cdots, X_{\mathcal{G}}^{(t+T)}\right] \in \mathbb{R}^{T \times N \times d \times C} X=[XG(t),⋯,XG(t+T)]∈RT×N×d×C为 h 0 = [ X G ( t ) , ⋯ , X G ( t + K ) ] ∈ R K × N × d × C h^{0}=\left[X_{\mathcal{G}}^{(t)}, \cdots, X_{\mathcal{G}}^{(t+K)}\right] \in \mathbb{R}^{K \times N \times d \times C} h0=[XG(t),⋯,XG(t+K)]∈RK×N×d×C后输入的时间维度。这边切割应该是为了让多个STFGN模块同时处理输入数据加快数据处理速度。
2.Spatial-Temporal Fusion Graph Neural Module
模块结构图如下:
在时空融合图神经模块中,轻量级深度学习模型可以通过矩阵乘法、残差连接和最大池化等简单操作提取隐藏的时空依赖关系。在STFGN模块中图形乘法模块的公式如下:
h l + 1 = ( A ∗ h l W 1 + b 1 ) ⊙ σ ( A ∗ h l W 2 + b 2 ) h^{l+1}=\left(A^{*} h^{l} W_{1}+b_{1}\right) \odot \sigma\left(A^{*} h^{l} W_{2}+b_{2}\right) hl+1=(A∗hlW1+b1)⊙σ(A∗hlW2+b2)
这边 h l h^{l} hl表示某个STFGN第l个隐藏状态,A*是ASTFG的缩写, W 1 , W 2 ∈ R C × C , b 1 , b 2 ∈ R C W_{1}, W_{2} \in \mathbb{R}^{\mathrm{C} \times \mathrm{C}}, b_{1}, b_{2} \in \mathbb{R}^{\mathrm{C}} W1,W2∈RC×C,b1,b2∈RC, ⊙ \odot ⊙是哈达玛乘积, σ \sigma σ表示sigmoid函数STFGN模块通过堆叠多个multiplication blocks聚集更复杂和非局部空间依赖。每个模块之间采取残差连接。最大池化被用于每个隐藏状态可以表示为: h M = MaxPool ( [ h 1 , ⋯ , h L ] ) ∈ R K × N × d × C h_M=\operatorname{MaxPool}\left(\left[h^{1}, \cdots, h^{L}\right]\right) \in \mathbb{R}^{K \times N \times d \times C} hM=MaxPool([h1,⋯,hL])∈RK×N×d×C,在池化层后为了减少参数数量作者进行了简直操作使 h o = h M [ ⌊ K 2 ⌋ : ⌊ K 2 ⌋ + 1 , : : : : : ] ∈ R 1 × N × d × C h^{o}=h^{M}\left[\left\lfloor\frac{K}{2}\right\rfloor:\left\lfloor\frac{K}{2}\right\rfloor+1,:::::\right] \in \mathbb{R}^{1 \times N \times d \times C} ho=hM[⌊2K⌋:⌊2K⌋+1,:::::]∈R1×N×d×C。输入数据会被多个STFGN模块同时处理。多个STFGN模块的输出级联后和Gated CNN的输出相加作为STFGN layer的最终输出和下以STFGN layer的输入。
这边需要注意的使每经过一层STFGN layer输入数据的时间维度将从T降到T-K+1(一个窗口大小为K的窗口每次移动一格最后输出维度为T-K+1),也就是每层减少了K-1个时间维度所以最多可以叠 ⌊ T K − 1 ⌋ − 1 \left\lfloor\frac{T}{K-1}\right\rfloor-1 ⌊K−1T⌋−1层STGFGN层。
3.Gated Convolution Module
虽然ASTFG可以通过集成ATG来提取全局时空相关性,但它包含的相关性更多地来自远处的节点。但是节点自身的长时间依赖也很重要,所以本文提出了一个具有打扩张率的扩张卷积。对于输入 X ∈ R T × N × d × C X \in \mathbb{R}^{T \times N \times d \times C} X∈RT×N×d×C操作如下:
Y = ϕ ( Θ 1 ∗ X + a ) ⊙ σ ( Θ 2 ∗ X + b ) Y=\phi\left(\Theta_{1} * X+a\right) \odot \sigma\left(\Theta_{2} * X+b\right) Y=ϕ(Θ1∗X+a)⊙σ(Θ2∗X+b)
其中 ϕ \phi ϕ和 σ \sigma σ分别代表tanh和sigmoid函数, Θ 1 , Θ 2 \Theta_{1},\Theta_{2} Θ1,Θ2是两个dilation rate为K-1的1D卷积。它可以沿时间轴扩大接受域,从而增强模型提取序列相关性的性能。本文使用Huber loss作为损失函数,具体函数如下:
L ( X ^ G ( t + 1 ) : ( t + T ) , Θ ) = ∑ i = 1 T ∑ j = 1 N ∑ k = 1 d h ( X ^ G ( t + i ) , X G ( t + i ) ) T × N × d L\left(\hat{\mathbf{X}}_{\mathcal{G}}^{(t+1):(t+T)}, \Theta\right)=\frac{\sum_{i=1}^{T} \sum_{j=1}^{N} \sum_{k=1}^{d} h\left(\hat{\mathbf{X}}_{\mathcal{G}}^{(t+i)}, \mathbf{X}_{\mathcal{G}}^{(t+i)}\right)}{T \times N \times d} L(X^G(t+1):(t+T),Θ)=T×N×d∑i=1T∑j=1N∑k=1dh(X^G(t+i),XG(t+i))
L ( X ^ G ( t + 1 ) : ( t + T ) , Θ ) = ∑ i = 1 T ∑ j = 1 N ∑ k = 1 d h ( X ^ G ( t + i ) , X G ( t + i ) ) T × N × d L\left(\hat{\mathbf{X}}_{\mathcal{G}}^{(t+1):(t+T)}, \Theta\right)=\frac{\sum_{i=1}^{T} \sum_{j=1}^{N} \sum_{k=1}^{d} h\left(\hat{\mathbf{X}}_{\mathcal{G}}^{(t+i)}, \mathbf{X}_{\mathcal{G}}^{(t+i)}\right)}{T \times N \times d} L(X^G(t+1):(t+T),Θ)=T×N×d∑i=1T∑j=1N∑k=1dh(X^G(t+i),XG(t+i))
δ是控制平方误差损失灵敏度的超参数。
5、Experiments
各个模型的比较:
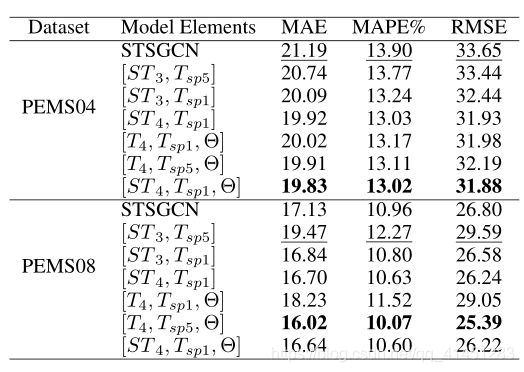
消融实验:
其中STn表示ASTFG的尺寸为K=4,T4表示将ASTFG中的ASG全部替换为ATG,Tsp1和Tsp5表示ATG中的零比率分别为0.01和0.05。
为K=4,T4表示将ASTFG中的ASG全部替换为ATG,Tsp1和Tsp5表示ATG中的零比率分别为0.01和0.05。