矩阵论体系简单梳理

基于本人在研一上学期的学习内容，以个人的视角，进行了一些梳理和解读。

摘要

矩阵理论作为一门应用广泛的数学基础课程，在很多行业、专业都有着重要的实用价值。所以对于这样的基础学科有必要进行系统学习，并应该掌握必要的应用方法。本文基于这样的学习目的，总结了矩阵理论的一些基础内容和应用。 包括矩阵论的基础理论、矩阵分解、矩阵分析、基础计算、Jordan 标准型等。本 文的贡献是总结了一张针对应用的矩阵理论基础框架逻辑图，涵盖了大部分科研工作中会涉及的相关概念、方法，不同于一般的知识框图，本文的工作更适用于 面向应用的角度。另外，本文也会列举一些在矩阵理论在图神经网络中的具体应用。

1 引言

随着科学技术的迅速发展，古典的线性代数知识已不能满足现代科技的需要， 矩阵的理论和方法业已成为现代科技领域必不可少的工具。诸如数值分析、优化 理论、微分方程、概率统计、控制论、力学、电子学、网络等学科领域都与矩阵 理论有着密切的联系，甚至在经济管理、金融、保险、社会科学等领域，矩阵理 论和方法也有着十分重要的应用。当今电子计算机及计算技术的迅速发展为矩阵 理论的应用开辟了更广阔的前景。因此，学习和掌握矩阵的基本理论和方法，对 于工科研究生来说是必不可少的。

本文正文分为四个章节，第二章用于介绍本文总结的矩阵论结构框架，并介绍其中的基础理论，包括线性空间、内积空间这两个矩阵理论的重要前提，也包 括矩阵分解这一应用的基本工具。第三章用于介绍特征值估计和 Jordan 标准型两大计算工具。第四章用于介绍矩阵分析，包括矩阵函数及相应的矩阵方程、矩 阵微分方程、广义逆等。在以上的理论介绍中将穿插应用的举例。最后在第五章 将提供一个 SVD 应用于图像压缩的实验。

本文的贡献在于，基于我们组内三位同学的汇报、哈工大严老师的课程、西北工业大学的教材《矩阵论》[1]以及 Gilbert Strang 的第五版教材《Introduction to linear Algebra》[2]总结出了面向应用的矩阵理论基础知识框架，囊括了大部分基础理论、计算理论。

2 矩阵基础理论

2.1 整体框图

经过学习和整理，本文按照应用的需求，站在应用的角度，将矩阵理论的基础内容总结到一张框架图中，如图 1。

图 1 矩阵理论整体理论框图

该框图分为三大部分，右侧黄色区域为基础理论，包括线性空间、内积空间两大基础前提。在每个空间下有相应的度量定义、运算定义等基础内容。同时还包括重要的矩阵分解，几乎囊括了全部的分解方法。右侧的绿色区域为两大计算工具：特征值估计与 Jordan 标准型，很多推论都是基于这两者而来。左侧蓝色区域为矩阵分析，包含矩阵函数为主的内容，这即是矩阵理论的高级用法，整体右侧为左侧基础，右侧的下方又为上方基础。结构上从下到上从右到左为递进逻辑， 也应是矩阵理论的学习顺序。下面讲依次介绍各部分内容。

2.2 基础理论

基础理论以线性空间开始，无论是线性代数还是矩阵理论的开端都是以线性空间起头的，这是要先确定讨论的前提，只有确定了问题发生的空间，统一了运算法则和度量规则，才能继续后面的讨论。首先基础部分的空间部分框图如图 2。

图 2 空间部分框图

线性空间是定义在域上的，所谓域就是一种代数系统，它可以做四则运算且对四则运算保持封闭。有理数域、实数域、复数域是常见的域，比如两个有理数相加、相乘等等还是有理数，但是整数集不是域，因为两个整数相除不一定是整数。线性空间中的元素没有形式上的限制，例如可以是多项式或者连续函数，我 们不关心所谓的向量是什么内容，只要它在运算上满足条件就可以。

在有了这样一个空间的基础上，我认为先要了解运算规则，因为有了规则， 才能对运算进行讨论。接着我们要明确对象，线性空间中有很多向量，一部分向 量可以看作一个有限序列，其实对于一组向量的处理也就是对于一组有限序列的处理。序列中的向量组下可划分子组，进而通过最大线性无关子组可求得一组向量，也就是一个矩阵的秩。这里的秩是一个并不陌生的概念。此处的解释默认建立在本科课程线性代数的基础之上。在一个矩阵中包含很多线性方程，有的是线性相关的，当去掉相关的向量，剩下的互不线性相关的方程的个数即为矩阵的秩。

在理解了秩的意义后，我们要利用秩来进行矩阵之间关系的判断，如果两个矩阵的秩相同，两矩阵相似，进而如果正负惯性指数相同，则两者合同，最后如果两者特征值相同，则两者等价。对于矩阵之间关系的判断也是应用中广泛涉及的问题，当所得两个矩阵等价时，我即可认为在欧式空间中两个矩阵所代表的点或平面重合。比如在做插值问题时，如何确定插值的起点与终点是否与目标吻合， 当经过计算两个矩阵并不能直接判断是否等价时，即可利用秩、特征值来判断两者的关系。

接着我们要有基的概念，把每个向量看作一个基坐标，也就是说一个或者几个向量即可确定一个基底，如果我要在一个空间中确定一个基底，并将其他所需向量映射到这个基底上时，即可进行相应的运算，这也为后面的矩阵分解做了一个基础。此处我们引入 Gram 矩阵，它是基向量组的度量矩阵，可以唯一确定一个向量组的内积。在图像处理中，可以看做 feature 之间的偏心协方差矩阵(即 没有减去均值的协方差矩阵)，在 feature map 中，每个数字都来自于一个特定滤波器在特定位置的卷积，因此每个数字代表一个特征的强度，而 Gram 计算的实际上是两两特征之间的相关性，哪两个特征是同时出现的，哪两个是此消彼长的等等，同时，Gram 的对角线元素，还体现了每个特征在图像中出现的量，因此， Gram 有助于把握整个图像的大体风格。有了表示风格的 Gram Matrix，要度量两个图像风格的差异，只需比较他们 Gram Matrix 的差异即可。Gram 矩阵可用于 度量各个维度自己的特性以及各个维度之间的关系。内积之后得到的多尺度矩阵中，对角线元素提供了不同特征图各自的信息，其余元素提供了不同特征图之间的相关信息。这样一个矩阵，既能体现出有哪些特征，又能体现出不同特征间的紧密程度。

我们有整体的空间概念，进而也可以推广到微观角度——向量空间的子空间， 向量空间的子空间需要满足：子空间内的向量进行相加相减，乘以或者除以一个 标量，或者子空间向量之间的线性组合得到的新向量还是位于该子空间中。

其实在此部分最重要的是有空间和基底的概念，这两个是我们的问题讨论基础。

其实内积空间是属于线性空间的，是一种特殊的线性空间。但这里要单独提出。此处需要涉及范数，这个是数值分析中已经涉及过的知识，此处便不做介绍直接使用。内积空间即是赋范的线性空间加上内积运算的空间，以此在空间中引入了角度的概念。内积空间有距离、长度、角度等，有限维的内积空间也就是我们熟悉的欧氏空间。欧式空间也是我们很多实验进行的基础。在内积空间中应用最多的是“投影定理”，也就是正交与投影，投影矩阵的应用如最小二乘、广义逆、 PCA 等。

2.3 矩阵分解

矩阵分解中在深度学习中使用最多的是 SVD 分解和其延伸的 PCA。在本小节将系统的概述全部分解方法，如图 3。

图 3 矩阵分解框图

特征值分解可以理解为方阵的奇异值分解(SVD)。在其中对称矩阵承担了基底的角色。对阵矩阵有一个性质：即把一组正交基映射为另一组正交基。对于任意的的矩阵 AA，AA 可以将 nn 维空间中的向量映射到 kk 维空间 中(k≤mk≤m)，那么现在来探究能否找到这样一组 nn 维正交基，使之经过 AA 的变换后，还是正交基。寻找这样正交基的过程，就是 SVD 的核心思路。在人 工智能中，PCA(主成分分析)是应用广泛的方法，它与 SVD 有着很多相似点。 两者都是矩阵分解的技术，一个直接分解 SVD，一个是对协方差矩阵操作后分 解 PCA；奇异值和特征向量存在关系，即有：。

SVD 可以获取另一个方向上的主成分，而 PCA 只能获得单个方向上的主成分， PCA 只与 SVD 的右奇异向量的压缩效果相同；通过 SVD 可以得到 PCA 相同的结果，但是 SVD 通常比直接使用 PCA 更稳定，因为在 PCA 求协方差时很可能会丢失一些精度。

3 计算基础

 本章介绍特征值估计和 Jordan 标准型两个计算工具。两者框图如图 4、5。

图 4 特征值估计框图

图 5 Jordan 标准型框图

 3.1 特征值估计

矩阵特征值是矩阵的重要参数之一。把矩阵对角化或者求矩阵的 Jordan 标准形、判别矩阵的收敛，以及矩阵函数的性质都与特征值有关。当矩阵的阶数高于五次时，没有求根公式，这个时候如果能够给出特征值的位置或者给出特征值 的取值范围，会对解决问题有一定的帮助。

不具体求特征值，而是给出特征值的范围，这就是特征值估计问题。例如讨论矩阵幂级数是否收敛，只要知道矩阵的谱半径是否小于幂级数的收敛半径即可。 在自动控制理论中，系统的稳定性与特征值的实数部分的符号有关，如果实数部分为负，则系统稳定。因此通过矩阵本身的数值来给出特征值的范围就显得很重要。

对于 n 阶非奇异方阵，有 n 个特征值。从宏观的思路出发，我们可以先确定整体特征值的上下界，对于复数域的矩阵，我们还需要分别考虑其特征值的实部和虚部。从微观角度出发，我们可以更深入的确定每个特征值的范围，如果这些范围有重叠，但我们可以通过相似矩阵具有相同特征值的特点设计对角阵来按比例缩放每个特征值的范围。在计算上下界中有四种方法，其中一种方法用到 schur 不等式；在计算特征值包含区域中，主要通过 Gerschorin 圆(盖尔圆)理论来划分特征值区域，盖尔圆的应用主要在于隔离特征值，该理论力求将每个特征值隔离到一个较小的范围内。

3.2 Jordan标准型

Jordan 标准型的证明和求解涉及到多项式矩阵和 Smith 标准型的内容。而 Jordan 标准型的应用价值在于，当两个矩阵并不能对角化，但还需要判定两者是否相似，而相似性问题的一个重点是研究矩阵的可对角化问题，此时就可把无法对角化矩阵的相似判断问题转化为求矩阵的 Jordan 标准形问题。在实际的应用中，面对的很多矩阵是无法对角化的，所以 Jordan 标准型在此起到了很大的作用。可以证明，任何一个方阵都可以找到对应的 Jordan 标准形，其关键问题是如何找到同阶的满秩方阵 P，使得。

4 矩阵分析

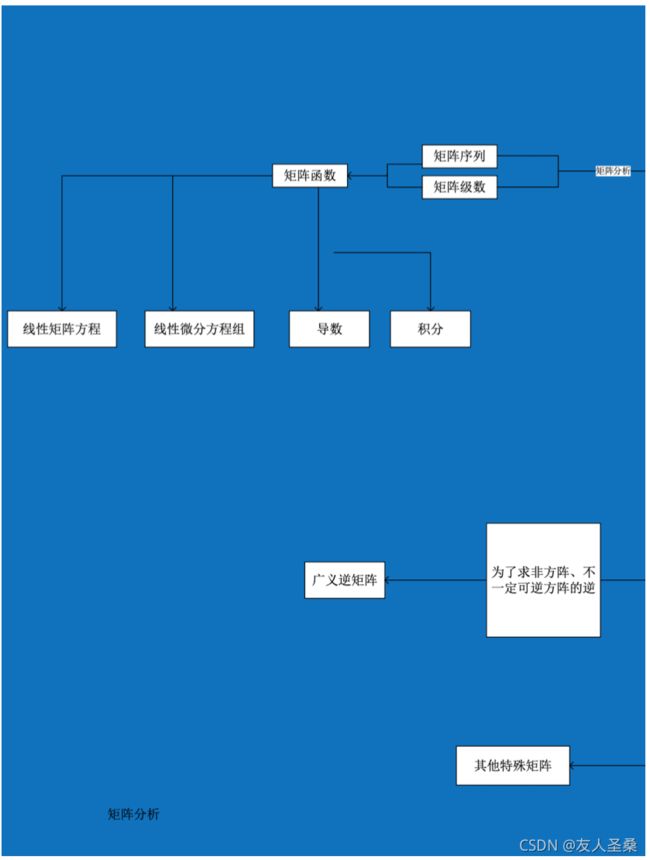
矩阵分析部分框图如图 6。该部分是利用前面所述内容进行应用的部分，此部分的重点在于矩阵方程的求解。

图6 矩阵分析框图

矩阵分析这一部分的目的就是将“矩阵”看作“数”，也就是每个矩阵都是一个元素， 就像我们普通代数中的数字一样，也可以建立方程、求解。这样便可引入更多的运算工具，也可以解决更多的数学问题。

该矩阵对于奇异矩阵甚至长方矩阵都存在、具有通常逆矩阵的一些性质、当矩阵非奇异时，它还原到通常的逆矩阵，满足以上 3 条性质的矩阵叫做广义逆矩阵。广义逆的作用是解决病态矩阵和一般矩阵的求逆问题。

5 应用举例

SVD 分解可用于图像压缩，下面将举例说明[3]。首先选取原始图片如图 7。

图7 人像实例

 这是一张人像。对该图片进行奇异值分解，则该图片可写成以下和的形式：

首先，若我们只保留最大的奇异值 λ1，舍去其它奇异值，作图 8(a)。接着取前五大奇异值，如图 8(b)。

图 8 舍去最大奇异值结果图；取 5 个奇异值结果图

图9 取50个奇异值结果图

最后取 50 个奇异值的结果如图 9。可见，取前 50 个最大奇异值来重构图像时，已经非常清晰了。我们得到和原图差别不大的图像。也就是说，随着选择的奇异值的增加，重构的图像越来越接近原图像。基于这个原理，奇异值分解可以用来进行图片压缩。例如在本例中，原始图片的维度是 870×870，总共需要保存的像素值是：870×870=756900。若使用 SVD，取前 50 个最大的奇异值即可，则总共需要存储的元素个数为 87050。

显然，所需存储量大大减小了。在需要存储许多高清图片，而存储空间有限的情况下，就可以利用 SVD，保留奇异值最大的若干项，舍去奇异值较小的项即可。值得一提的是，奇异值从大到小衰减得特别快，在很多情况下，前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了。

6 结论

本文章简要的从应用角度出发，按照从简入深的逻辑顺序，分三大块介绍了矩阵理论中的重要内容。本文分别介绍了作为讨论基础的空间，作为大矩阵求逆工具的矩阵分解，作为运算工具的特征值和 Jordan 标准型，最后将以上基本方法推广到了矩阵函数的求解。本文并为包含定理的证明，因为这些已在教材中有所体现，本文的目的是理清关系和构建体系框架，使面向应用的矩阵理论知识可以构成一个逻辑整体。在最后的 SVD 图像压缩实验则是对于理论结合实际的应用展示。

参考文献

[1] 程云鹏，张凯院，徐仲. 矩阵论[M]. 第 4 版. 西安:西北工业大学出版社，2017.

[2] Gilbert Strang. Introduction to Linear Algebra[M]. 5 edition. 北京:清华大学出 版社，2019.

[3] visionshop. 详解 SVD 分解过程[EB/OL]. https://blog.csdn.net/u012968002/article/details/91354566