决策树(Decision Tree)算法 python简单实现
1. 简介
决策数(Decision Tree)在机器学习中是比较常见的一种算法,属于监督学习中的一种。
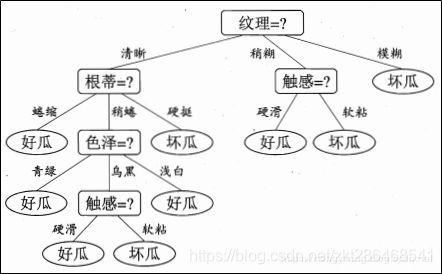
算法流程如图:

具体算法可以详见下方参考 有空再做详解
参考:https://blog.csdn.net/zaishuiyifangxym/article/details/96630813
2.代码实现
"""
Created on Thu Nov 28 14:01:04 2019
@author: alpha
"""
import numpy as np
from math import log
import operator
import json
#生成海洋生物数据
def createData():
data = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels=['不浮出水面可生存','脚蹼']
return data, labels
#生产西瓜数据
# =============================================================================
# 色泽: 浅白 青绿 乌黑
# 根蒂: 蜷缩 稍蜷 硬挺
# 敲声: 浊响 沉闷 清脆
# 纹理: 清晰 稍糊 模糊
# 脐部: 凹陷 稍凹 平坦
# 触感: 硬滑 软粘
# =============================================================================
def createWatermelonData():
data = [['青绿','蜷缩','浊响','清晰','凹陷','硬滑','好'],
['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','好'],
['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','好'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','好'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑','好'],
['青绿','稍蜷','浊响','清晰','稍凹','软粘','好'],
['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','好'],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','好'],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','坏'],
['青绿','硬挺','清脆','清晰','平坦','软粘','坏'],
['浅白','硬挺','清脆','模糊','平坦','硬滑','坏'],
['浅白','蜷缩','浊响','模糊','平坦','软粘','坏'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','坏'],
['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','坏'],
['乌黑','稍蜷','浊响','清晰','稍凹','软粘','坏'],
['浅白','蜷缩','浊响','模糊','平坦','硬滑','坏'],
['青绿','蜷缩','沉闷','模糊','稍凹','硬滑','坏']]
labels=['色泽','根蒂','敲声','纹理','脐部','触感']
return data, labels
#计算熵
def calcEnt(data):
num = len(data)
labelCounts = {}
for item in data:
label = item[-1]
if label not in labelCounts.keys():labelCounts[label] = 0
labelCounts[label] += 1
ent = 0
for key in labelCounts:
prob = labelCounts[key]*1.0/num
ent -= prob * log(prob,2)
return ent
#划分数据 根据某一特征axis 取出该特征某一特定值value的数据
def splitData(dataSet,axis,value):
retData=[]
for item in dataSet:
if item[axis]==value:
newItem = item[:axis]
newItem.extend(item[axis+1:])
retData.append(newItem)
return retData
#从特种中选择最好的方式 增益最高
def chooseBestFeature(dataSet):
numFeat = len(dataSet[0]) - 1
## 初始化 信息熵 最佳信息增益 最佳特征
baseEnt = calcEnt(dataSet)
bestGain = 0
bestFeat = -1
for i in range(numFeat):
##获取第i个特征的所有取值
uniFeats = set([item[i] for item in dataSet])
newEnt = 0
##计算按第i个特征分类的熵
for value in uniFeats:
##第i个特征值 value的概率
subData = splitData(dataSet,i,value)
prob = float(len(subData))/len(dataSet)
newEnt += prob * calcEnt(subData)
gain = baseEnt - newEnt
if gain>bestGain:
bestGain = gain
bestFeat = i
return bestFeat
## 返回类别最高的分类
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
#建立表
def createTree(dataSet,labels):
classList = [item[-1] for item in dataSet]
##只包含一种分类 返回该分类
if len(set(classList))==1:
return classList[0]
if len(dataSet[0])==1:
return majorityCnt(classList)
bestFeat = chooseBestFeature(dataSet)
bestFeatLabel = labels[bestFeat]
##以最佳分类标签为节点 以字典形式保存
myTree={bestFeatLabel:{}}
del(labels[bestFeat])
uniFeats = set([item[bestFeat] for item in dataSet])
for value in uniFeats:
subLabels = labels[:]
##根据不同的value 继续建立子分支
myTree[bestFeatLabel][value] = createTree(splitData(dataSet,bestFeat,value),subLabels)
return myTree
data,labels = createWatermelonData()
ret=createTree(data,labels)
print(json.dumps(ret,sort_keys=True, indent=2,ensure_ascii=False))
最终输出的结果如下
{
"纹理": {
"模糊": "坏",
"清晰": {
"根蒂": {
"硬挺": "坏",
"稍蜷": {
"色泽": {
"乌黑": {
"触感": {
"硬滑": "好",
"软粘": "坏"
}
},
"青绿": "好"
}
},
"蜷缩": "好"
}
},
"稍糊": {
"触感": {
"硬滑": "坏",
"软粘": "好"
}
}
}
}