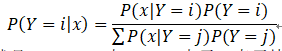分类算法原理及python实现(一)
文章目录
- 一、分类算法的概念
-
- 1.概念
- 2.应用
- 3.统计学分类与机器学习分类的区别
- 4. 概率模型与非概率模型基本思想
- 二、分类算法
-
- 1.逻辑回归
- 2.朴素贝叶斯
- 3.K近邻
一、分类算法的概念
1.概念
输出变量Y为有限个离散值的预测问题,是一种有监督学习。分类算法可以分为概率模型与非概率模型,概率模型通过学习得到属性集与分类标签的条件概率分布形式P(y|x),非概率模型通过学习得到一个属性集与分类标签的函数形式y=f(x)
2.应用
分类模型可以被用于预测类别未知的个体的类别标签,也可以根据分类模型解释样本分类规律等
3.统计学分类与机器学习分类的区别
统计学分类与机器学习分类的主要区别在于,统计学模型重点是刻画数据与结果变量之间的关系,而不是对未知个体进行预测;机器学习模型的重点是模型在与模型的预测精度,往往会牺牲掉模型的可解释性追求更高的精度。
因此对应到分类问题中,统计学分类更关注分类模型的可解释性,通过解释模型中的参数提取出数据中的分类规律(个体因为具备了哪些属性所以被分到了某一类);而机器学习分类更多的关注模型的预测效果(模型是个否能够准确预测未知个体的类别)。
4. 概率模型与非概率模型基本思想
分类学习算法可以分为两类:概率模型与非概率模型。概率模型的基本思想是求条件概率P(Y│x),选择概率最大值对应的类别作为分类结果,以获得最小的经验风险;非概率模型的基本思想是直接拟合输入向量x与输出类别y之间的映射关系。

二、分类算法
1.逻辑回归
定义:Logistic Regression逻辑回归属于概率模型,一个单独的逻辑回归只能用于二分类问题(类别用0,1表示),逻辑回归模型如下,其中x为输入的特征向量,ω,b为参数,
P(Y=1│x)=(exp(ωx+b))/(1+exp(ωx+b))
P(Y=0│x)=1/(1+exp(ωx+b))
可以看到对于给定的输入实例x,逻辑回归会得到该实例属于0或1的概率,并将实例x分到概率值较大的一类。
原理及推导:
明确目标:已知x求P(Y=1│x)
思考解决办法:找到一个x→p的映射f,即找到一个函数f满足自变量可以取任意值,因变量为一个概率值。
具体解决过程:
首先需要引入一个概念,一个事件发生的几率(Odds)是指该事件发生的概率与不发生的概率的比值,那么假设该事件发生的概率为p,那么该事件的几率为
对该事件发生的几率取对数即为logit函数,该函数的特点是定义域为(0,1),值域为R,
我们的目标是求概率p,所以取logit函数的反函数,得到sigmoid函数
对于逻辑回归有,
其中α可以取任意值且一定要与输入实例x联系起来,逻辑回归中取α=ωx+b,即
参数估计
逻辑回归利用极大似然估计法估计模型参数
设
则似然函数为
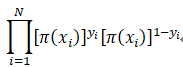
对似然函数取对数后,得到对数似然函数,再求其极大值,即可得到ω的估计值。
逻辑回归Python实现
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.metrics import accuracy_score
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:100, 2:4]
y = iris.target[:100]
X_train, X_test, y_train, y_test =\
train_test_split(X, y, test_size=0.20, random_state=0)
# Create an instance of Logistic Regression Classifier and fit the data
logreg = LogisticRegression(C=1)
logreg.fit(X_train, y_train)
LogisticRegression(C=1)
y_pred = logreg.predict(X_test)
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))
2.朴素贝叶斯
定义:基于贝叶斯定理与特征条件独立假设的分类方法,对于给定的训练集,首先基于特征独立假设学习输入与输出的联合概率分布;然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y.
原理及推导
明确目标:已知x求P(Y=i│x)
所以我们要求的就是P(x|Y=i)与P(x),由于x表示特征向量,假设
![]()
每一个特征有k_h (h=1,2,⋯,n)种可能取值,类别数为n,容易得出待求参数P(x|Y=i)共有
![]()
为了减少待求参数,朴素贝叶斯方法提出了特征条件独立的假设,该假设也正是朴素贝叶斯朴素之处。在特征条件独立的假设下,该算法的待求参数量减少到了![]()
参数估计:直接用训练数据集的频率估计概率。
适用范围及优缺点
由于朴素贝叶斯的特征条件独立假设,所以该模型比较适用于特征量较少的小数据集(特征量小独立性假设成立的可能性大)。
朴素贝叶斯很明显的优点就是简单易用,在特征独立假设成立的数据集上表现较好;当然,特征独立性假设也使得朴素贝叶斯适用条件比较苛刻。
朴素贝叶斯算法Python实现
import numpy as np
from sklearn.naive_bayes import GaussianNB # naive bayes
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.metrics import accuracy_score
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:100, 2:4]
y = iris.target[:100]
X_train, X_test, y_train, y_test =\
train_test_split(X, y, test_size=0.20, random_state=0)
# Create Naive Bayes classifier
classifier = GaussianNB()
# Train the classifier
classifier.fit(X_train, y_train)
# Predict the values
y_pred = classifier.predict(X_test)
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))
3.K近邻
定义:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
原理及推导
明确目标:已知x,求Y=f(x)
思考解决办法:从训练集中找到与输入实例x最相似的实例x’,根据x’所属的类别来确定输入实例x的类别。为了减小误差以及尽可能的利用训练集数据所提供的信息,我们进一步改进算法,从训练集中选取与输入实例最邻近的k个实例,按照多数表决的思想,将k个相似实例中出现次数最多的类别作为输入实例x的类别。
那么问题是如何根据特征向量判断两个实例的相似性?以及k值如何取?
距离度量
我们利用两个实例点的距离来反映两个实例点的相似程度。这个距离可以是欧式距离、Lp距离或曼哈顿距离等。
设
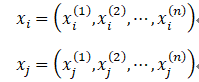
则xi ,xj的Lp距离定义为
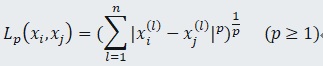
当p=2时,称为欧式距离,p=1时称为曼哈顿距离
k值选取
K值的选择会对k近邻算法产生很大的影响。
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,那么只有与输入实例较为相似的训练实例才会对预测结果起作用,但同时预测结果会对近邻的实例点非常敏感。
如果k值太大,就相当于用较大邻域中的训练实例进行预测。其优点是预测结果对某一个实例不会非常敏感,但同时预测结果可能会受到一些与输入实例不相关的点的影响,比如当k值取最大值,即训练集的实例个数N时,无论输入实例是什么都会被分到出现次数最多的类别中。
因此k值应该选择一个比较适中的值,一般情况下,我们会先取一个较小的数值,然后逐步增大,根据模型评估结果来选择最优的k值。
K近邻算法python实现
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.metrics import accuracy_score
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:100, 2:4]
y = iris.target[:100]
X_train, X_test, y_train, y_test =\
train_test_split(X, y, test_size=0.20, random_state=0)
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
clf = KNeighborsClassifier(n_neighbors=5)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))