【可解释机器学习】-线性回归案例【lasso特征选择版】(python)
阅读本文前需要先阅读:【可解释机器学习】-线性回归案例【基础版】
可解释机器学习:黑盒模型可解释性理解指南
作者: 【德】 Christoph Molnar
出版社: 电子工业出版社
译者: 朱明超英文版(作者在持续更新):Interpretable Machine Learning
原书github:GitHub - christophM/interpretable-ml-book: Book about interpretable machine learning
注意:原书使用R语言,本文的Python代码为我自己开发。内容基本参考原书,我进行了结构调整,并且添加了自己的理解和其他书籍的知识。
本文在【基础版】上做了以下变化(蓝色):
本案例模型简述
模型:最基础的多元线性归回
特征选择:lasso选择特征
特征交互:无
本案例数据集简述
目标变量:自行车租赁量,连续型,因此为回归问题
分类特征处理方式: 进行one-hot编码,其中未出现的取值(例如春、晴)作为参照类别
连续特征处理方式:使用原始值(不进行标准化和归一化)
lasso要点
为什么使用lasso:当特征数量过多,线性回归模型的解释能力就会下降。lasso使用L1范数对权重加大惩罚,可以使很多权重的估计值为0。如何选择正则化参数λ:将其视为一个优化参数,通过交叉验证找到模型预测效果+保留特征数量均合适的值。
进行lasso选择时特征构造要求:分类型使用one-hot编码时保留参照类别;由于添加了惩罚项,特征集需要统一进行z-score标准化。
本案例中,lasso仅作为特征选择的工具,后续将lasso选择的k个特征代入线性模型(流程参考基础线性回归模型),特别注意分类特征的入选。
目录
第0节:数据集处理
第一节:使用lasso进行特征选择
1.1.进行z-score标准化
1.2.运行lasso
1.3.以正则化参数为x轴,特征数量、评估指标为双y轴画图
1.4.参照图,找到模型预测效果+保留特征数量均合适的正则化参数值
1.5.确定最终入选特征
第二节:进行线性回归
2.1.检验多重共线性和目标变量正态性
2.2.建模
第一,将权重表的值组合为一个DataFrame
第二, 对比实例的真实值、预测值、置信区间,并画图
第一步:观察模型拟合效果。
第二步:文本解释特征(数值型和分类型有不同的文本模板)。
第三步:解释截距。
第四步:解释特征重要性。
第五步:进一步可视化解释权重。
第六步:可视化效应图。
第七步:通过效应图解释单个实例。
第0节:数据集处理
import numpy as np
import pandas as pd
import time #统计运行时间用
import copy #深拷贝的时候用
import _pickle as cPickle
import gc #释放内存使用
from tqdm import tqdm,tqdm_notebook #Tqdm 是一个快速,可扩展的Python进度条
import datetime #处理时间数据
import os
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_squared_error,roc_auc_score,log_loss
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator, FormatStrFormatter
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
import seaborn as sns
%matplotlib inline
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
warnings.filterwarnings("ignore")
pd.set_option('display.max_columns',100)
pd.set_option('max_colwidth',100)
path='../data/'
#原始数据集
bike=pd.read_csv(path+'Bike-Sharing-Dataset/day.csv',parse_dates=['dteday'])
#目前下载的原始数据,季节被更新了,无法与作者书中的数字保持一致,因此导入旧数据集
bike_oldseason=pd.read_csv(path+'Bike-Sharing-Dataset/bike_oldseason.csv' )
bike['season']=bike_oldseason['season'].map({'WINTER':1,'SPRING':2,'SUMMER':3,'FALL':4})
bike.head()
#添加特征days_since_2011,自数据集中第一天(20110101)起的天数),引入此特征为了考虑随时间变化的趋势
bike['days_since_2011']= (bike['dteday']-min(bike['dteday'])).dt.days
#原始数据集中的几个特征进行了标准化,这里还原到原始值
# denormalize weather features:
# temp : Normalized temperature in Celsius. The values are derived via (t-t_min)/(t_max-t_min), t_min=-8, t_max=+39 (only in hourly scale)
bike['temp'] = bike['temp'] * (39 - (-8)) + (-8)
# windspeed: Normalized wind speed. The values are divided to 67 (max)
bike['windspeed'] = 67 * bike['windspeed']
# hum: Normalized humidity. The values are divided to 100 (max)
bike['hum'] = 100 * bike['hum']
#保留的特征:租赁数量cnt(目标变量),季节,是否假期(1是,0不是),是否工作日(1是,0不是),天气情况(晴、雾、雨雪),温度(单位为℃),湿度(相对湿度百分比0~100%),风速(单位为km/h),天数
select_cols=['cnt','season','holiday', 'workingday', 'weathersit', 'temp', 'hum', 'windspeed', 'days_since_2011']
bike=bike[select_cols]
bike.to_csv(path+'处理完数据集/bike.csv',index=False,encoding='utf_8_sig')
def f_ohe(df,col,new_names=None,keep_cate='auto'):
'''
【功能】对一个特征进行独热编码
【参数】df:dataframe,数据集
col:str,需要进行独热编码的特征名
new_names: dic,如果需要对取值重命名(使特征名更能表达真实意思),则新建一个字典,默认None则特征名为col_取值
keep_cate: list,需要保留的取值,如果取值是数值型则需要先排序,例如[[1,3,4]];默认'auto'表示保留所有值
【返回】dataframe
【举例】t_season=f_ohe(df=bike,col='season',new_names={1:'冬',3:'夏',4:'秋'},keep_cate=[[1,3,4]])
'''
ohe=OneHotEncoder(dtype=np.int8,handle_unknown='ignore',sparse=False,categories=keep_cate)
ohe.fit(df[col].values.reshape(-1,1))
tmp=pd.DataFrame(ohe.transform(df[col].values.reshape(-1,1)))
org_names=ohe.get_feature_names_out([col]).tolist() #col作为新生成字段的前缀
if new_names is None:
tmp.columns=org_names
else:
new_names_keys=list(new_names.keys()) #获取输入的keys
new_names_keys=[col+'_'+str(item) for item in new_names_keys] #输入的keys加上col前缀
# print(new_names_keys)
new_names=dict(zip(new_names_keys,list(new_names.values()))) #加上前缀的keys和输入的values重新打包为字典
# print(new_names)
a=list(pd.Series(data=org_names).map(new_names).values) #list不能直接map,把原特征名map转为Series后映射为新特征名
tmp.columns=[col+'_'+str(item) for item in a] #加上col前缀
return tmp
#对于取值有两类的特征(是否假期holiday、是否工作日workingday),由于本身已是0/1编码,因此不作进一步处理
#对于取值>2类的特征(季节season、天气情况weathersit),进行one-hot编码
path='../data/'
bike=pd.read_csv(path+'处理完数据集/bike.csv')
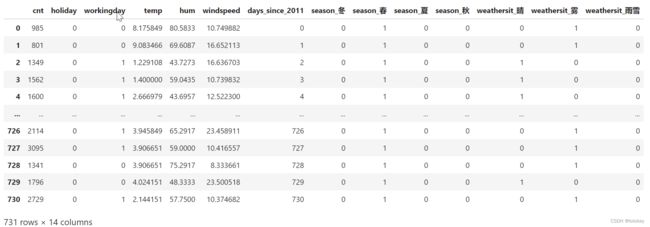
bike
#季节,全部类别保留
t_season=f_ohe(df=bike,col='season',new_names={1:'冬',2:'春',3:'夏',4:'秋'},keep_cate='auto')
#天气情况,全部类别保留
t_weathersit=f_ohe(df=bike,col='weathersit',new_names={1:'晴',2:'雾',3:'雨雪'},keep_cate='auto')
bike_ohe_comp=pd.concat((bike[['cnt','holiday', 'workingday', 'temp', 'hum', 'windspeed', 'days_since_2011']],
t_season,t_weathersit),axis=1)
bike_ohe_comp
bike_ohe_comp.to_csv(path+'处理完数据集/bike_ohe_comp.csv',index=False,encoding='utf_8_sig')path='../data/'
bike_ohe_comp=pd.read_csv(path+'处理完数据集/bike_ohe_comp.csv')
bike_ohe_comp
df=bike_ohe_comp
label='cnt'
feas=df.columns.tolist()
feas.remove(label)
print('特征数量:',len(feas))
X_train=df[feas]
y_train=df[label]
print('X_train:',X_train.shape)
print('y_train:',y_train.shape)第一节:使用lasso进行特征选择
1.1.进行z-score标准化
scaler = StandardScaler() # 标准化 z = (x - u) / s
X_train_std = pd.DataFrame(scaler.fit_transform(X_train))
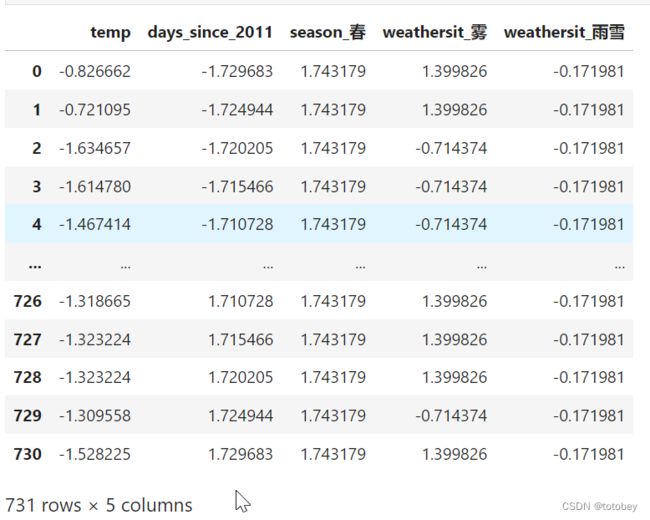
X_train_std.columns=X_train.columns
X_train_std1.2.运行lasso
def select_feas_lasso(trainX,trainy,metric_name='rmse',kfNum=2):
'''
【功能说明】
【参数】trainX:DataFrame,训练集的特征部分,需要先进行标准化,one-hot编码需要保留参照类别
trainy:Series,训练集的标签列
metric_name:str,评估指标,默认'rmse',可选'logloss','auc'
kfNum:int,>=2,默认2,交叉验证轮数
【返回】字典,包含参数array,评估指标均值、标准差,保留特征数均值、标准差
【举例】scaler = StandardScaler() # 标准化 z = (x - u) / s
X_train_std = pd.DataFrame(scaler.fit_transform(X_train))
res=select_feas_lasso(trainX=X_train_std,trainy=y_train,metric_name='rmse',kfNum=2)
lasso_alphas=res['lasso_alphas']
valid_scores=res['valid_scores']
keep_var_nums=res['keep_var_nums']
【版本】V1.0
'''
s=time.time()
print('\n********lasso_select_feas...start')
print('评估指标:',metric_name)
print('交叉验证轮数:',kfNum)
print('训练集形状:',trainX.shape,type(trainX))
#对于#0.001-100,使用logspace
lasso_alphas1 = np.logspace(start=-3, stop=2, num=50, base=10) #0.001-100
#对于比较大的lambda,使用整数步长
lasso_alphas2 = np.arange(start=100,stop=1000,step=20)
lasso_alphas= np.concatenate((lasso_alphas1, lasso_alphas2))
print('待计算正则化参数数量:',len(lasso_alphas))
print('待计算正则化参数最小值:',np.min(lasso_alphas))
print('待计算正则化参数最大值:',np.max(lasso_alphas))
valid_scores = [] #存储每个正则化参数下的评估指标均值如rmse
keep_var_nums = [] #存储每个正则化参数下保留的特征数量均值
valid_scores_std = [] #标准差
keep_var_nums_std = [] #标准差
for alpha in tqdm(lasso_alphas):
clf = Lasso(max_iter=1000,random_state=2020,alpha=alpha)
kf=KFold(n_splits=kfNum, shuffle=True, random_state=2020)
valid_score=[] #存储每轮交叉验证的评估指标如rmse
keep_var_num=[] #存储每轮交叉验证保留特征数量
for i,(trn_index,val_index) in enumerate(kf.split(trainX,trainy)): #i从0开始,可以显示第几轮了
trn_df=trainX.iloc[trn_index]
val_df=trainX.iloc[val_index]
trn_y=trainy.iloc[trn_index]
val_y=trainy.iloc[val_index]
clf.fit(X=trn_df, y=trn_y)
#利用本轮模型预测本轮验证集
valid_pred=clf.predict(val_df)
#-------计算本轮评估指标--------#
if metric_name == 'rmse':
valid_score_this=mean_squared_error(val_y,valid_pred,squared=True)
elif metric_name == 'logloss':
valid_score_this=log_loss(y_true=val_y,y_pred=valid_pred)
elif metric_name == 'auc':
valid_score_this=roc_auc_score(y_true=val_y,y_score=valid_pred)
else:
print('亲,没这评估指标')
return
valid_score.append(valid_score_this) #列表append后直接替换原对象,所以不用再赋值
# print(valid_score)
keep_var_num=sum(clf.coef_ != 0) #统计系数不为0的特征数量(不含截距)
# print(keep_var_num)
valid_scores.append(np.mean(valid_score)) #metric取均值,存入
keep_var_nums.append(np.mean(keep_var_num)) #保留特征数量取均值,存入
valid_scores_std.append(np.std(valid_score)) #metric取标准差,存入
keep_var_nums_std.append(np.std(keep_var_num)) #保留特征数量取均值取标准差,存入
res={'lasso_alphas':lasso_alphas,
'valid_scores':valid_scores,'valid_scores_std':valid_scores_std,
'keep_var_nums':keep_var_nums,'keep_var_nums_std':keep_var_nums_std}
return res
res=select_feas_lasso(trainX=X_train_std,trainy=y_train,metric_name='rmse',kfNum=2)1.3.以正则化参数为x轴,特征数量、评估指标为双y轴画图
lasso_alphas=res['lasso_alphas']
valid_scores=res['valid_scores']
keep_var_nums=res['keep_var_nums']
mertic_name='RMSE'
fig = plt.figure(figsize=(18, 8))
ax1=fig.add_subplot(111)
ax1.plot(lasso_alphas,keep_var_nums, "b-o",label='特征数量') #画出折线并且添加实心圆点
ax1.set_ylabel('特征数量',fontsize=20)
ax1.grid(True) #显示网格线
xmajorLocator = MultipleLocator(100) # x轴刻度间隔 100
ymajorLocator = MultipleLocator(1) # y轴刻度间隔 1
ax1.yaxis.set_major_locator(ymajorLocator)
ax1.xaxis.set_major_locator(xmajorLocator)
plt.xlabel('正则化参数',fontsize=18) #添加x轴名称
ax2 = ax1.twinx()
ax2.plot(lasso_alphas,valid_scores, "r-D",label=mertic_name) #画出折线并且添加实心菱形
ax2.set_ylabel(mertic_name,fontsize=20)
ax1.legend(loc='center left',fontsize=15) #添加图例
ax2.legend(loc='center right',fontsize=15)
plt.title('lasso',fontsize=30)
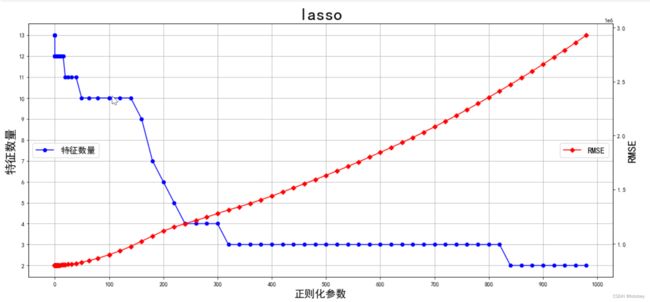
plt.show()1.4.参照图,找到模型预测效果+保留特征数量均合适的正则化参数值
### 保留5个变量(示例)
# 由于画图使用的是交叉验证,后续用的是全量实例,因此正则化参数值可能会有微小区别。
# 以上图的正则化参数值220为基础,调试后将其设定为250
# 找到保留的5个变量
best_clf = Lasso(max_iter=1000,random_state=2020,alpha=250)
best_clf.fit(X=X_train_std, y=y_train)
coef=pd.Series(best_clf.coef_,index=best_clf.feature_names_in_)
coef1.5.确定最终入选特征
连续型变量直接入选(temp、days_since_2011 )
上表中,季节中只有春季入选,因此其他三个季节(非春季)统一构成参照类别。这与基础线性回归时将春单独作为参照类别有很大不同,后续进行模型解释时要特别注意
上表中,天气情况入选的为晴、雨雪,最终选择雾、雨雪。变更后本质一样,只是将参照类别从雾变更为了晴以提高可解释性
#连续型变量直接入选(temp、days_since_2011 )
#上表中,季节中只有春季入选,因此其他三个季节(非春季)统一构成参照类别。这与基础线性回归时将春单独作为参照类别有很大不同,后续进行模型解释时要特别注意
#上表中,天气情况入选的为晴、雨雪,最终选择雾、雨雪。变更后本质一样,只是将参照类别从雾变更为了晴以提高可解释性
keep_var5=['temp','days_since_2011','season_春','weathersit_雾','weathersit_雨雪']第二节:进行线性回归
df=bike_ohe_comp
label='cnt'
feas=df.columns.tolist()
feas.remove(label)
print('特征数量:',len(feas))
X_train=df[keep_var5]
y_train=df[label]
print('X_train:',X_train.shape)
print('y_train:',y_train.shape)2.1.检验多重共线性和目标变量正态性
def checkVIF(df):
'''
【功能】计算方差膨胀因子
【参数】df:dataframe,特征集(不含target)
【返回】dataframe,展示各个特征的VIF
【参考】当0=100,'严重多重共线性',np.where(VIF['VIF']>=10,'较强多重共线性','无多重共线性'))
return VIF
def checkNORM(se,p=0.05,alt='two-sided',if_plot=True):
'''
【功能】检验一组数据是否符合正态分布
【参数】se:Series
p:float,p值,默认0.05
alt:str,默认双侧检验'two-sided',可选'less', 'greater'
if_plot,是否画图,默认True
【返回】dataframe,展示各个特征的VIF
【参考】结果返回两个值:statistic → D值,pvalue → P值
【备注】import matplotlib.pyplot as plt
%matplotlib inline
【举例】 res=checkNORM(y_train)
'''
from scipy import stats
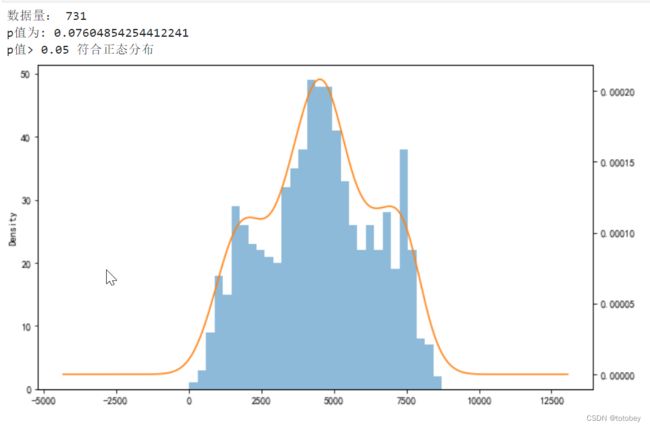
print('数据量:',len(se))
u = se.mean() # 计算均值
std = se.std() # 计算标准差
res=stats.kstest(rvs=se, cdf='norm',args= (u, std), alternative=alt)
print('p值为:',res[1])
if res[1]>p:
print('p值>',p,'符合正态分布')
else:
print('p值<=',p,'不符合正态分布')
if if_plot==True:
fig = plt.figure(figsize = (10,6))
se.hist(bins=30,alpha = 0.5) #直方图 alpha表示透明度
se.plot(kind = 'kde', secondary_y=True) #核密度估计KDE
plt.show()
return res
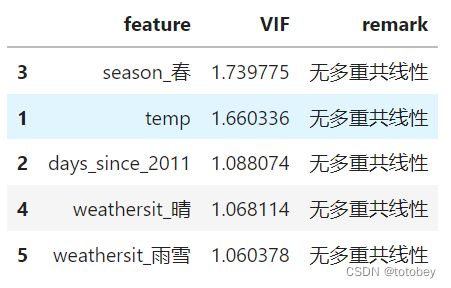
VIF1=checkVIF(X_train)
VIF1
res=checkNORM(y_train) 2.2.建模
from statsmodels.regression.linear_model import OLS,GLS #Ordinary least squares普通最小二乘法
import statsmodels.formula.api as smf
import statsmodels.api as sm
#建模方式1:使用smf.ols,自己编写formula,会自动添加常数列
#cnt为目标变量,分类特征可使用C(season)进行编码,由于本数据集的分类特征都已事先编码,因此不需要添加c()
model=smf.ols(formula='cnt ~ season_春 + weathersit_雾 + weathersit_雨雪 + temp + days_since_2011 ',data=df)
results=model.fit()
results.summary()第一,将权重表的值组合为一个DataFrame
df_coef=pd.DataFrame(results.params ) #权重
df_coef.columns=['coef']
df_coef['lw']=results.conf_int(alpha=0.05)[0].values #获取权重的置信区间下限
df_coef['up']=results.conf_int(alpha=0.05)[1].values #获取权重的置信区间上限
df_coef['SE']=results.bse.values #权重的标准误std err
df_coef['t']=results.tvalues.values #权重的t统计量,等于权重/标准误
df_coef['p']=results.pvalues.values #参数的t统计的双尾 p 值
df_coef['t_abs']=abs(df_coef['t']) #求绝对值
#根据已有的权重和置信区间计算上下误差,计算完毕后发现上下误差相同
df_coef['lw_err']=df_coef['coef']-df_coef['lw']
df_coef['up_err']=df_coef['up']-df_coef['coef']
df_coef
第二, 对比实例的真实值、预测值、置信区间,并画图
#获取置信区间的上下限
pred_ols = results.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
#results.fittedvalues为模型预测值
target_df=pd.concat((y_train,results.fittedvalues,iv_l,iv_u),axis=1)
target_df.columns=['true','predict','ci_lower','ci_upper']
target_df['resid']=results.resid #残差
target_df
#按实际租赁量排序,reset_index是必须的
plot_df=target_df.sort_values(['true']).reset_index(drop=True)
fig, ax = plt.subplots(figsize=(20, 9))
ax.plot(plot_df['true'], "b-", label="True")
ax.plot(plot_df['predict'], "r", label="Pred")
# ax.plot(plot_df['ci_lower'], "r--",alpha=0.5) #置信区间虚线
# ax.plot(plot_df['ci_upper'], "r--",alpha=0.5) #置信区间虚线
plt.fill_between(plot_df.index,plot_df['ci_lower'],plot_df['ci_upper'],color='blue',alpha=0.15)
ax.legend(loc="best")
plt.ylabel('自行车租赁量',fontsize=18)
plt.title('真实值与预测值对比',fontsize=20)
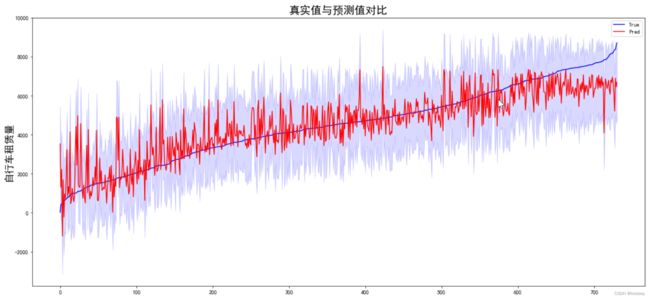
plt.show()
上图中,蓝线为真实值,红色实线为预测值,蓝紫色为置信区间。
由上图可知,左侧租赁量较小时,部分预测值远高于真实值且波动较大;右侧租赁量较大时,预测值整体偏低。
由此图也可以看出,前文中提到的线性回归模型的【同方差性】在现实中是很难满足的。
本案例数据量较小,如果数据量较大,可以随机抽样后再画图。
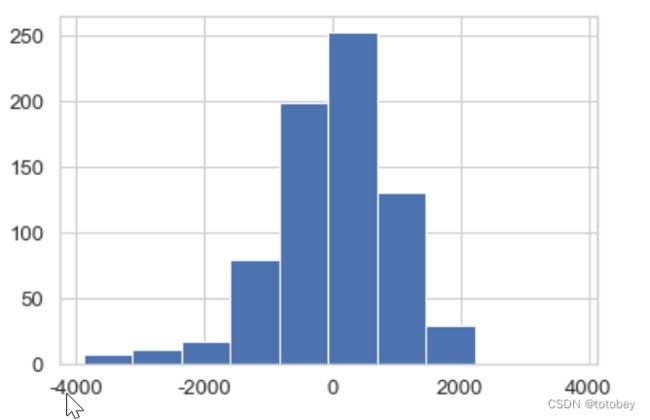
#残差——同方差性
#1.应该为均值是0的正态分布
sns.set(style="whitegrid",font_scale=1.2)#设置主题,文本大小
plt.hist(target_df['resid'])
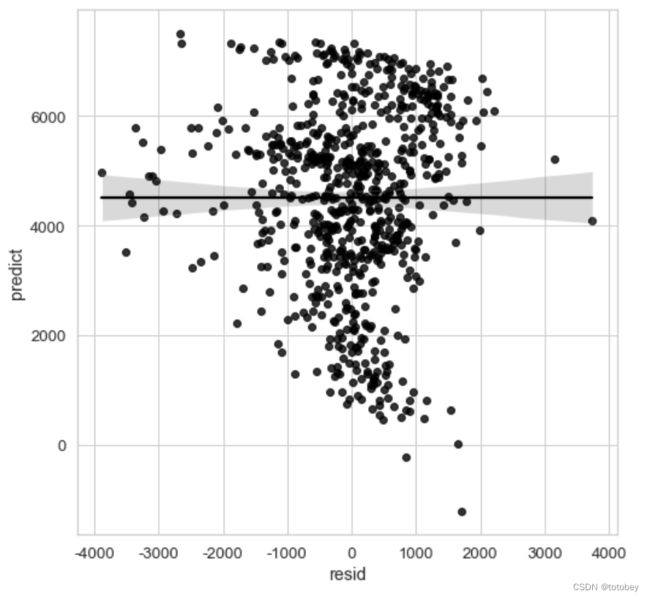
plt.show()#2.残差与predict之间应该不相关
#regplot默认参数线性回归图
plt.figure(figsize=(8, 8))
sns.set(style="whitegrid",font_scale=1.2)#设置主题,文本大小
g=sns.regplot(x='resid', y='predict', data=target_df,
color='#000000',#设置marker及线的颜色
# marker='*',#设置marker形状
)下面进行模型解释。
第一步:观察模型拟合效果。
观察调整后R方(解释一个该值很低的模型是没有意义的,对权重的任何解释都没有意义)。
该模型的调整后R方是0.756,表示该模型解释了目标结果75.6%的总方差,拟合度较优。
未进行特征选择的模型调整后R方是0.79,为了提高可解释性(减少特征数量),牺牲了一部分的模型预测准确度。
第二步:文本解释特征(数值型和分类型有不同的文本模板)。
数值特征文本模板:当所有其他特征保持不变时,特征x增加一个单位,则预测结果y增加β。
分类特征文本模板:当所有其他特征保持不变时,将特征x从参照类别改变为其他类别时,预测结果y会增加β。
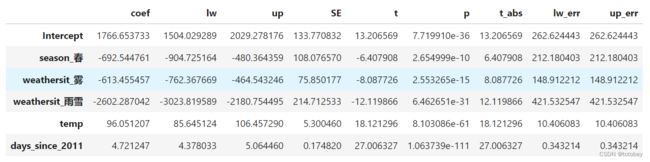
观察权重(上图中coef列)(由于本数据集使用了原始值,即未进行标准化和归一化,因此可以直接进行表述):
温度(数值特征):当所有其他特征保持不变时,将温度升高1℃,自行车的预测数量增加96辆(基础线性回归为110,近似)。
季节(分类特征):所有其他特征保持不变,春季的自行车租赁量比其他三个季节少了692辆(注意,由于只有春季入选,因此其他三个季节(非春季)统一构成参照类别)。
第三步:解释截距。
截距权重:对所有数值特征为0和分类特征为参照类别的实例,模型预测值即为截距的权重。上述解释通常没有意义(特征全部为0 的实例通常无实际含义)。但是,当特征标准化(均值为0,标准差为1)时,这种解释将会有实际含义,此时截距反应所有特征都处于均值时实例的预测结果。
本例中,截距的权重为2399,表示当处于非春季、晴天,温度为0,且为2011年1月1号时,预测的自行车数量为1766辆。以上解释无实际意义。
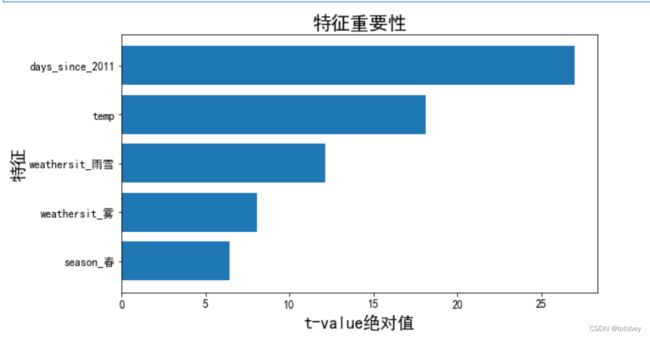
第四步:解释特征重要性。
使用t-统计量的绝对值解释特征重要性,(t=权重/SE,其中SE是标准误)。特征的重要性随着权重的增加而增加,随着方差的增加而减小(方差越大表明对正确值的把握越小)。
本例中,t统计量已经被计算出来了,上图中的t=coef/std err。
plot_df=df_coef.drop(index='Intercept') #删除截距行
plot_df=plot_df.sort_values(['t_abs']) #排序
fig = plt.figure(figsize = (9,5))
plt.barh(plot_df.index,plot_df['t_abs']) #画水平条形图
#设置x轴y轴
plt.xlabel('t-value绝对值',fontsize=18)
plt.ylabel('特征',fontsize=18)
plt.xticks(fontsize=12) #放大横纵坐标刻度线上的特征名字体
plt.yticks(fontsize=12)
plt.title('特征重要性',fontsize=20)
plt.show()由上图可知,最重要的特征为距离2011年第一天的天数,排名第二的为温度,排名第三的为是否是雨雪天气(与基础线性回归排名一致)
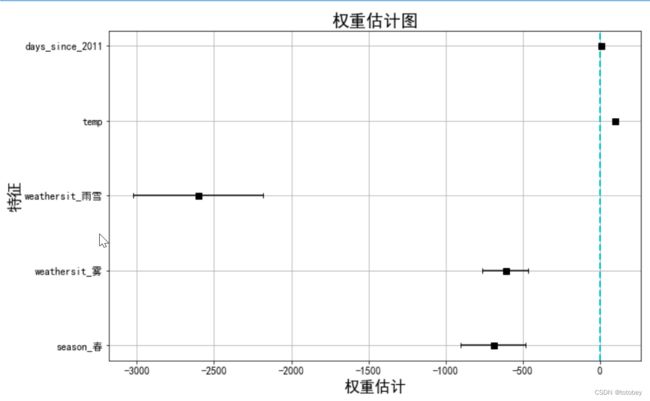
第五步:进一步可视化解释权重。
第二步已通过文本解释了权重(coef)的实际含义,这一步根据权重和置信区间画权重图。
plot_df=df_coef.drop(index='Intercept') #删除截距行
fig = plt.figure(figsize = (11,7))
#由于上下误差相同,因此直接用 xerr=plot_df['lw_err'],否则可以使用xerr=plot_df[['lw_err','up_err']].T.values来分别规定上下限
plt.errorbar(x=plot_df['coef'], y=plot_df.index,xerr=plot_df['lw_err'], color="black", capsize=3,
linestyle="None",
marker="s", markersize=7, mfc="black", mec="black")
plt.grid(True) #显示网格线
plt.xlabel('权重估计',fontsize=18)
plt.ylabel('特征',fontsize=18)
plt.xticks(fontsize=12) #放大横纵坐标刻度线上的特征名字体
plt.yticks(fontsize=12)
plt.title('权重估计图',fontsize=20)
plt.axvline(c="c",ls="--",lw=2) #原点竖线
plt.show()由上图可知:
1.雨雪天气对自行车租赁量有很大的负效应。
2.天数、温度的置信区间很短,估计值接近于0,但特征效应在统计上是显著的。
3.如果某特征的权重接近于0,并且95%的置信区间包含0,这表明该效应在统计上不显著。(基础线性回归中有是否工作日)
权重图的问题:
各个特征的量纲不一样,比如天气情况反映了晴天和雨雪天的差异,但是温度只反映了1℃的变化情况。
因此可以通过在建模前对特征进行标准化(均值为0,标准差为1),使估计的权重更具有可比性。
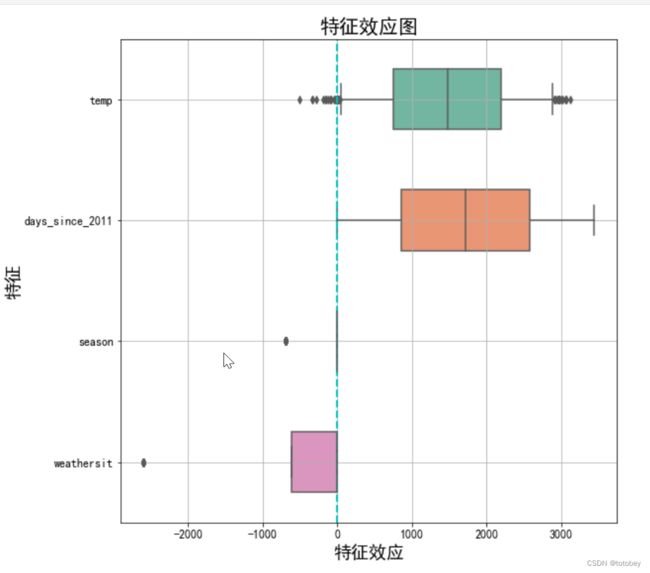
第六步:可视化效应图。
效应图(effect plot)帮助了解权重和特征的组合对数据预测的贡献程度。特征效应为每个特征的权重乘以实例的特征值。如改变特征的量纲,则权重会发生变化,但特征效应不会改变。
通过画箱线图(注意,分类特征总结为一个箱线图),可以观察下面几个方面:1)特征效应的正负性;2)特征效应的绝对值大小;3)特征效应的方差(如果方差小,则意味着这个特征几乎在所有实例中都有类似的贡献)。
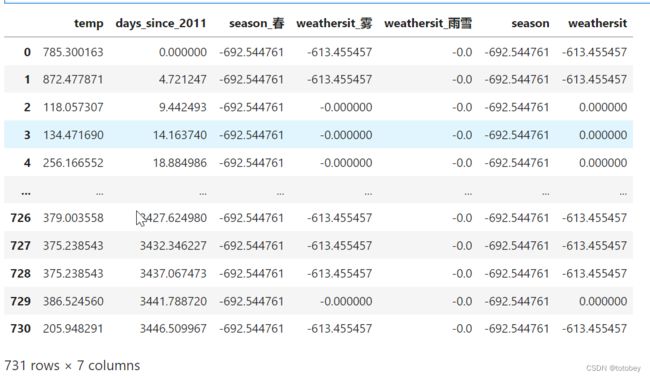
#求特征效应——每个特征的权重乘以实例的特征值
w=df_coef['coef'].values
w_order=[] #将特征权重与实例中的顺序一一对应
my_dict={0:4,1:5,2:1,3:2,4:3} #权重表与数据集中特征的对应顺序
for i in range(5):
w_order.insert(i,w[my_dict[i]])
#计算特征效应
effect=X_train*w_order
#分类特征合并
effect['season']=np.sum(effect[['season_春']],axis=1)
effect['weathersit']=np.sum(effect[['weathersit_雾','weathersit_雨雪']],axis=1)
effectplt.subplots(figsize=(9, 9))
cols=[ 'temp', 'days_since_2011',
'season', 'weathersit']
sns.boxplot(data=effect[cols],orient="h",width=0.5,whis=0.5, palette="Set2")
plt.grid(True) #显示网格线
plt.xlabel('特征效应',fontsize=18)
plt.ylabel('特征',fontsize=18)
plt.xticks(fontsize=12) #放大横纵坐标刻度线上的特征名字体
plt.yticks(fontsize=12)
plt.title('特征效应图',fontsize=20)
plt.axvline(c="c",ls="--",lw=2) #原点竖线
plt.show()由上图可知:
1.对预测自行车租赁数量正向贡献最大的来自温度和天数。
2.天气的情况参照类别为晴天,图中说明除了晴天外的天气(雾、雨雪)都会对自行车租赁量产生负向影响。
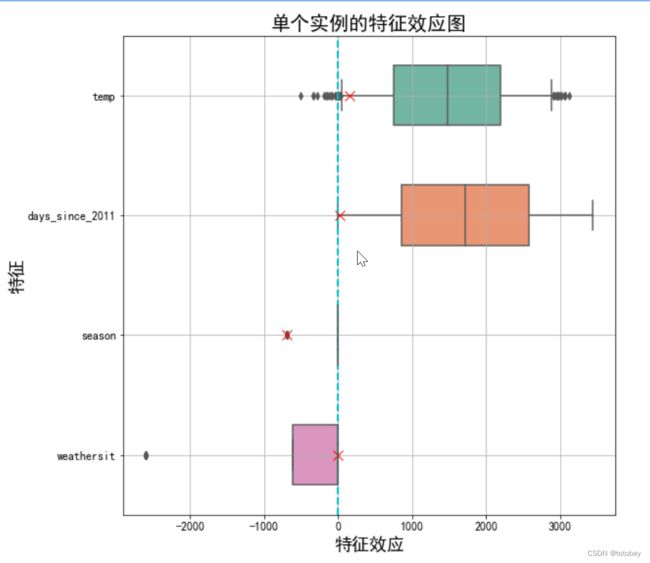
第七步:通过效应图解释单个实例。
通过计算单个实例的特征效应,可以得到这个实例的各个特征对预测有多大的贡献。
步骤1:得到这个实例的预测值、所有实例的平均预测值、这个实例的实际值。将这个实例的预测值与所有实例的平均预测值进行对比,如果差距很大,则进一步解释原因。
步骤2:计算这个实例的特征效应,然后加入第六步的特征效应图中。即将这个实例的特征效应与所有实例的特征效应分布进行比较,得出结论。
single_idx=5 #第6个实例
print(bike_ohe.loc[single_idx])
target_predict=target_df.loc[single_idx,'predict']
target_predict_mean=np.mean(target_df['predict'])
target_true=target_df.loc[single_idx,'true']
print('该实例预测值',target_predict)
print('所有实例平均预测值',target_predict_mean)
print('该实例实际值',target_true)plt.subplots(figsize=(9, 9))
cols=[ 'temp', 'days_since_2011',
'season', 'weathersit']
sns.boxplot(data=effect[cols],orient="h",width=0.5,whis=0.5, palette="Set2")
plt.grid(True) #显示网格线
plt.xlabel('特征效应',fontsize=18)
plt.ylabel('特征',fontsize=18)
plt.xticks(fontsize=12) #放大横纵坐标刻度线上的特征名字体
plt.yticks(fontsize=12)
plt.title('单个实例的特征效应图',fontsize=20)
plt.axvline(c="c",ls="--",lw=2) #原点竖线
#画单个实例中每个特征的效应
for col in cols:
col_index=cols.index(col) #获取某个特征在特征名列表的索引位置
plt.plot(effect.loc[single_idx,col], col_index,'rx', ms=10) #rx 红色叉号,ms控制大小
plt.show()以数据集中第6个实例为例:
相较于所有实例的平均预测值4504辆,该实例的预测值很小,只有1251辆自行车被租赁。效应图揭示了原因:
1.该实例温度的特征效应较小,这一天温度仅为1.6℃,与其他大多数日期的温度相比较低(温度权重为正)。
2.该实例天数的特征效应也较小,该实例自第一天起仅过了5天(天数权重为正)。
参考:statsmodels模块的fit_regularized实现lasso
# 参考:statsmodels模块的fit_regularized实现lasso
from statsmodels.regression.linear_model import OLS,GLS #Ordinary least squares普通最小二乘法
import statsmodels.formula.api as smf
import cvxopt #lasso需要 凸优化模块
import statsmodels.api as sm
#建模方式1:使用smf.ols,自己编写formula,会自动添加常数列
#cnt为目标变量,分类特征可使用C(season)进行编码,由于本数据集的分类特征都已事先编码,因此不需要添加c()
model=smf.ols(formula='cnt ~ season_夏 + season_秋 + season_冬 + holiday + workingday +weathersit_雾 + weathersit_雨雪 + temp + hum + windspeed +days_since_2011 ',data=df)
results=model.fit_regularized(method='sqrt_lasso',alpha=10)
results