一文了解数据异常值检测方法
异常值检测方法作为数据分析过程中的重要一步,也是数据分析师的必备技能之一。下面简单介绍一下数据分析相关的检测方法,如有不足还请批评指正。
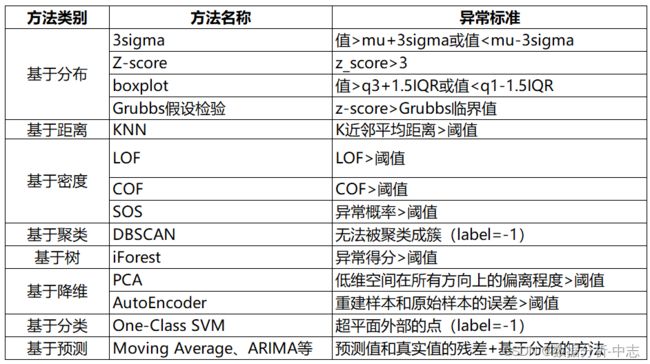
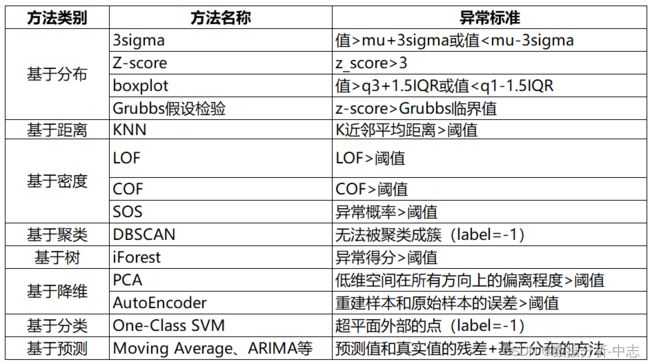
一、基于分布的异常值检测方法
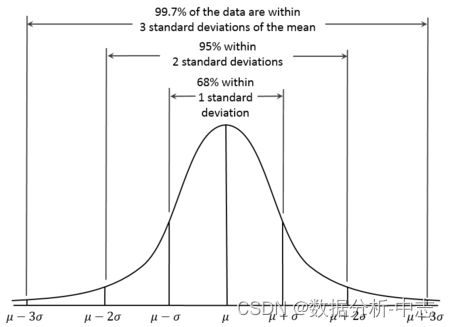
1. 3sigma
基于正态分布,3sigma准则认为超过3sigma的数据为异常点。
python程序实现:
def three_sigma(s):
mu, std = np.mean(s), np.std(s)
lower, upper = mu-3*std, mu+3*std
return lower, upper
2.Z-score
Z-score为标准分数,测量数据点和平均值的距离,若A与平均值相差2个标准差,Z-score为2。当把Z-score=3作为阈值去剔除异常点时,便相当于3sigma。
def z_score(s):
z_score = (s - np.mean(s)) / np.std(s)
return z_score
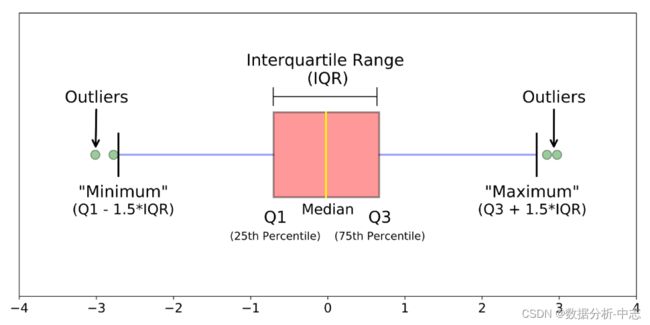
3. boxplot
def boxplot(s):
q1, q3 = s.quantile(.25), s.quantile(.75)
iqr = q3 - q1
lower, upper = q1 - 1.5*iqr, q3 + 1.5*iqr
return lower, upper
4.Grubbs假设检验
Grubbs’Test为一种假设检验的方法,常被用来检验服从正态分布的单变量数据集(univariate data set)Y中的单个异常值。若有异常值,则其必为数据集中的最大值或最小值。原假设与备择假设如下:
● H0: 数据集中没有异常值
● H1: 数据集中有一个异常值
使用Grubbs测试需要总体是正态分布的。算法流程:
1,样本从小到大排序
2,求样本的mean和dev
3, 计算min/max与mean的差距,更大的那个为可疑值
4,求可疑值的z-score (standard score),如果大于Grubbs临界值,那么就是outlier
Grubbs临界值可以查表得到,它由两个值决定:检出水平α(越严格越小),样本数量n,排除outlier,对剩余序列循环做 1-4 步骤 [1]。详细计算样例可以参考。
from outliers import smirnov_grubbs as grubbs
print(grubbs.test([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.min_test_outliers([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.max_test_outliers([8, 9, 10, 1, 9], alpha=0.05))
print(grubbs.max_test_indices([8, 9, 10, 50, 9], alpha=0.05))
局限:
1、只能检测单维度数据
2、无法精确的输出正常区间
3、它的判断机制是“逐一剔除”,所以每个异常值都要单独计算整个步骤,数据量大吃不消。
4、需假定数据服从正态分布或近正态分布
二、基于距离的异常值检测方法
1、KNN
依次计算每个样本点与它最近的K个样本的平均距离,再利用计算的距离与阈值进行比较,如果大于阈值,则认为是异常点。优点是不需要假设数据的分布,缺点是仅可以找出全局异常点,无法找到局部异常点。
from pyod.models.knn import KNN
# 初始化检测器clf
clf = KNN( method='mean', n_neighbors=3, )
clf.fit(X_train)
# 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_train_pred = clf.labels_
# 返回训练数据上的异常值 (分值越大越异常)
y_train_scores = clf.decision_scores_
三、基于密度的方法
1、 Local Outlier Factor (LOF)
LOF是基于密度的经典算法(Breuning et. al. 2000),通过给每个数据点都分配一个依赖于邻域密度的离群因子 LOF,进而判断该数据点是否为离群点。它的好处在于可以量化每个数据点的异常程度(outlierness)。
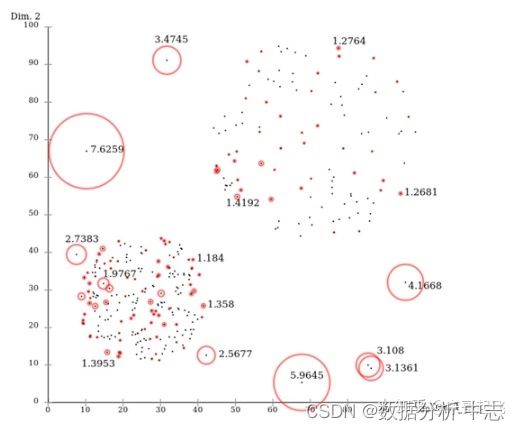
数据点P的局部相对密度(局部异常因子)=点P邻域内点的平均局部可达密度 跟 数据点P的局部可达密度 的比值: 数据点P的局部可达密度=P最近邻的平均可达距离的倒数。距离越大,密度越小。
点P到点O的第k可达距离=max(点O的k近邻距离,点P到点O的距离)。
整体来说,LOF算法流程如下:
● 对于每个数据点,计算它与其他所有点的距离,并按从近到远排序;
● 对于每个数据点,找到它的K-Nearest-Neighbor,计算LOF得分。
from sklearn.neighbors import LocalOutlierFactor as LOF
X = [[-1.1], [0.2], [100.1], [0.3]]
clf = LOF(n_neighbors=2)
res = clf.fit_predict(X)
print(res)
print(clf.negative_outlier_factor_)
2.Connectivity-Based Outlier Factor (COF)
COF是LOF的变种,相比于LOF,COF可以处理低密度下的异常值,COF的局部密度是基于平均链式距离计算得到。在一开始的时候我们一样会先计算出每个点的k-nearest neighbor。而接下来我们会计算每个点的Set based nearest Path,如下图:

假使我们今天我们的k=5,所以F的neighbor为B、C、D、E、G。而对于F离他最近的点为E,所以SBN Path的第一个元素是F、第二个是E。离E最近的点为D所以第三个元素为D,接下来离D最近的点为C和G,所以第四和五个元素为C和G,最后离C最近的点为B,第六个元素为B。所以整个流程下来,F的SBN Path为{F, E, D, C, G, C, B}。而对于SBN Path所对应的距离e={e1, e2, e3,…,ek},依照上面的例子e={3,2,1,1,1}。
所以我们可以说假使我们想计算p点的SBN Path,我们只要直接计算p点和其neighbor所有点所构成的graph的minimum spanning tree,之后我们再以p点为起点执行shortest path算法,就可以得到我们的SBN Path。
而接下来我们有了SBN Path我们就会接着计算,p点的链式距离: 有了ac_distance后,我们就可以计算COF:
from pyod.models.cof import COF
cof = COF(contamination = 0.06, ## 异常值所占的比例
n_neighbors = 20, ## 近邻数量
)
cof_label = cof.fit_predict(iris.values) # 鸢尾花数据
print("检测出的异常值数量为:",np.sum(cof_label == 1))
3.Stochastic Outlier Selection (SOS)
将特征矩阵(feature martrix)或者相异度矩阵(dissimilarity matrix)输入给SOS算法,会返回一个异常概率值向量(每个点对应一个)。SOS的思想是:当一个点和其它所有点的关联度(affinity)都很小的时候,它就是一个异常点。
-
计算相异度矩阵D;
-
计算关联度矩阵A;
-
计算关联概率矩阵B;
-
算出异常概率向量。
相异度矩阵D是各样本两两之间的度量距离,比如欧式距离或汉明距离等。关联度矩阵反映的是度量距离方差,如图7,点 的密度最大,方差最小; 的密度最小,方差最大。而关联概率矩阵B(binding probability matrix)就是把关联矩阵(affinity matrix)按行归一化得到的,如图8所示。

上图为关联度矩阵中密度可视化,下图为关联概率矩阵

得到了binding probability matrix,每个点的异常概率值就用如下的公式计算,当一个点和其它所有点的关联度(affinity)都很小的时候,它就是一个异常点。
import pandas as pd
from sksos import SOS
iris = pd.read_csv("http://bit.ly/iris-csv")
X = iris.drop("Name", axis=1).values
detector = SOS()
iris["score"] = detector.predict(X)
iris.sort_values("score", ascending=False).head(10)
四:基于聚类的方法
DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise)的输入和输出如下,对于无法形成聚类簇的孤立点,即为异常点(噪声点)。
● 输入:数据集,邻域半径Eps,邻域中数据对象数目阈值MinPts;
● 输出:密度联通簇。
-
从数据集中任意选取一个数据对象点p;
-
如果对于参数Eps和MinPts,所选取的数据对象点p为核心点,则找出所有从p密度可达的数据对象点,形成一个簇;
-
如果选取的数据对象点 p 是边缘点,选取另一个数据对象点;
-
重复以上2、3步,直到所有点被处理。
from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],
[8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
clustering.labels_
array([ 0, 0, 0, 1, 1, -1])
# 0,,0,,0:表示前三个样本被分为了一个群
# 1, 1:中间两个被分为一个群
# -1:最后一个为异常点,不属于任何一个群
五、基于树的方法
孤立森林中的 “孤立” (isolation) 指的是 “把异常点从所有样本中孤立出来”,论文中的原文是 “separating an instance from the rest of the instances”。
我们用一个随机超平面对一个数据空间进行切割,切一次可以生成两个子空间。接下来,我们再继续随机选取超平面,来切割第一步得到的两个子空间,以此循环下去,直到每子空间里面只包含一个数据点为止。我们可以发现,那些密度很高的簇要被切很多次才会停止切割,即每个点都单独存在于一个子空间内,但那些分布稀疏的点,大都很早就停到一个子空间内了。所以,整个孤立森林的算法思想:异常样本更容易快速落入叶子结点或者说,异常样本在决策树上,距离根节点更近。
随机选择m个特征,通过在所选特征的最大值和最小值之间随机选择一个值来分割数据点。观察值的划分递归地重复,直到所有的观察值被孤立。

获得 t 个孤立树后,单棵树的训练就结束了。接下来就可以用生成的孤立树来评估测试数据了,即计算异常分数 s。对于每个样本 x,需要对其综合计算每棵树的结果,通过下面的公式计算异常得分: ● h(x):为样本在iTree上的PathLength;
● E(h(x)):为样本在t棵iTree的PathLength的均值;
● c(n):为n个样本构建一个二叉搜索树BST中的未成功搜索平均路径长度(均值h(x)对外部节点终端的估计等同于BST中的未成功搜索)。 是对样本x的路径长度h(x)进行标准化处理。H(n-1)是调和数,可使用ln(n-1)+0.5772156649(欧拉常数)估算。 指数部分值域为(−∞,0),因此s值域为(0,1)。当PathLength越小,s越接近1,此时样本为异常值的概率越大。
from sklearn.datasets import load_iris
from sklearn.ensemble import IsolationForest
data = load_iris(as_frame=True)
X,y = data.data,data.target
df = data.frame
# 模型训练
iforest = IsolationForest(n_estimators=100, max_samples='auto',
contamination=0.05, max_features=4,
bootstrap=False, n_jobs=-1, random_state=1)
# fit_predict 函数 训练和预测一起 可以得到模型是否异常的判断,-1为异常,1为正常
df['label'] = iforest.fit_predict(X)
# 预测 decision_function 可以得出 异常评分
df['scores'] = iforest.decision_function(X)
六、基于降维的方法
1、Principal Component Analysis (PCA)
PCA在异常检测方面的做法,大体有两种思路:
(1) 将数据映射到低维特征空间,然后在特征空间不同维度上查看每个数据点跟其它数据的偏差;
(2) 将数据映射到低维特征空间,然后由低维特征空间重新映射回原空间,尝试用低维特征重构原始数据,看重构误差的大小。
PCA在做特征值分解,会得到:
● 特征向量:反应了原始数据方差变化程度的不同方向;
● 特征值:数据在对应方向上的方差大小。
所以,最大特征值对应的特征向量为数据方差最大的方向,最小特征值对应的特征向量为数据方差最小的方向。原始数据在不同方向上的方差变化反应了其内在特点。如果单个数据样本跟整体数据样本表现出的特点不太一致,比如在某些方向上跟其它数据样本偏离较大,可能就表示该数据样本是一个异常点。
在前面提到第一种做法中,样本 x i x_i xi的异常分数为该样本在所有方向上的偏离程度: 其中, 为样本在重构空间里离特征向量的距离。若存在样本点偏离各主成分越远, 会越大,意味偏移程度大,异常分数高。 是特征值,用于归一化,使不同方向上的偏离程度具有可比性。
在计算异常分数时,关于特征向量(即度量异常用的标杆)选择又有两种方式:
● 考虑在前k个特征向量方向上的偏差:前k个特征向量往往直接对应原始数据里的某几个特征,在前几个特征向量方向上偏差比较大的数据样本,往往就是在原始数据中那几个特征上的极值点。
● 考虑后r个特征向量方向上的偏差:后r个特征向量通常表示某几个原始特征的线性组合,线性组合之后的方差比较小反应了这几个特征之间的某种关系。在后几个特征方向上偏差比较大的数据样本,表示它在原始数据里对应的那几个特征上出现了与预计不太一致的情况。 得分大于阈值C则判断为异常。
第二种做法,PCA提取了数据的主要特征,如果一个数据样本不容易被重构出来,表示这个数据样本的特征跟整体数据样本的特征不一致,那么它显然就是一个异常的样本:
其中, 是基于k维特征向量重构的样本。
基于低维特征进行数据样本的重构时,舍弃了较小的特征值对应的特征向量方向上的信息。换一句话说,重构误差其实主要来自较小的特征值对应的特征向量方向上的信息。基于这个直观的理解,PCA在异常检测上的两种不同思路都会特别关注较小的特征值对应的特征向量。所以,我们说PCA在做异常检测时候的两种思路本质上是相似的,当然第一种方法还可以关注较大特征值对应的特征向量。
rom sklearn.decomposition import PCA
pca = PCA()
pca.fit(centered_training_data)
transformed_data = pca.transform(training_data)
y = transformed_data
# 计算异常分数
lambdas = pca.singular_values_
M = ((y*y)/lambdas)
# 前k个特征向量和后r个特征向量
q = 5
print "Explained variance by first q terms: ", sum(pca.explained_variance_ratio_[:q])
q_values = list(pca.singular_values_ < .2)
r = q_values.index(True)
# 对每个样本点进行距离求和的计算
major_components = M[:,range(q)]
minor_components = M[:,range(r, len(features))]
major_components = np.sum(major_components, axis=1)
minor_components = np.sum(minor_components, axis=1)
# 人为设定c1、c2阈值
components = pd.DataFrame({'major_components': major_components,
'minor_components': minor_components})
c1 = components.quantile(0.99)['major_components']
c2 = components.quantile(0.99)['minor_components']
# 制作分类器
def classifier(major_components, minor_components):
major = major_components > c1
minor = minor_components > c2
return np.logical_or(major,minor)
results = classifier(major_components=major_components, minor_components=minor_components)
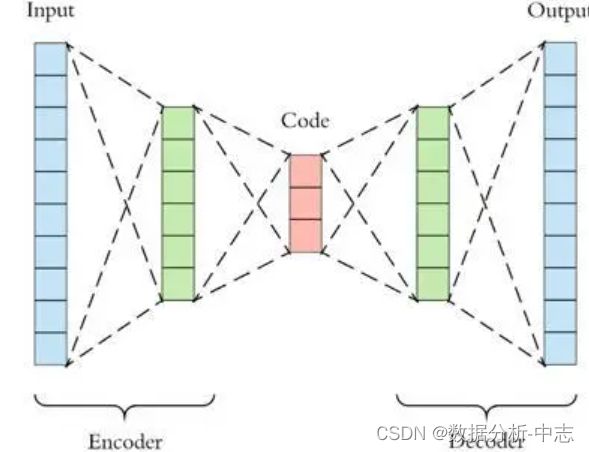
2、AutoEncoder
PCA是线性降维,AutoEncoder是非线性降维。根据正常数据训练出来的AutoEncoder,能够将正常样本重建还原,但是却无法将异于正常分布的数据点较好地还原,导致还原误差较大。因此如果一个新样本被编码,解码之后,它的误差超出正常数据编码和解码后的误差范围,则视作为异常数据。需要注意的是,AutoEncoder训练使用的数据是正常数据(即无异常值),这样才能得到重构后误差分布范围是多少以内是合理正常的。所以AutoEncoder在这里做异常检测时,算是一种有监督学习的方法。
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
# 标准化数据
scaler = preprocessing.MinMaxScaler()
X_train = pd.DataFrame(scaler.fit_transform(dataset_train),
columns=dataset_train.columns,
index=dataset_train.index)
# Random shuffle training data
X_train.sample(frac=1)
X_test = pd.DataFrame(scaler.transform(dataset_test),
columns=dataset_test.columns,
index=dataset_test.index)
tf.random.set_seed(10)
act_func = 'relu'
# Input layer:
model=Sequential()
# First hidden layer, connected to input vector X.
model.add(Dense(10,activation=act_func,
kernel_initializer='glorot_uniform',
kernel_regularizer=regularizers.l2(0.0),
input_shape=(X_train.shape[1],)
)
)
model.add(Dense(2,activation=act_func,
kernel_initializer='glorot_uniform'))
model.add(Dense(10,activation=act_func,
kernel_initializer='glorot_uniform'))
model.add(Dense(X_train.shape[1],
kernel_initializer='glorot_uniform'))
model.compile(loss='mse',optimizer='adam')
print(model.summary())
# Train model for 100 epochs, batch size of 10:
NUM_EPOCHS=100
BATCH_SIZE=10
history=model.fit(np.array(X_train),np.array(X_train),
batch_size=BATCH_SIZE,
epochs=NUM_EPOCHS,
validation_split=0.05,
verbose = 1)
plt.plot(history.history['loss'],
'b',
label='Training loss')
plt.plot(history.history['val_loss'],
'r',
label='Validation loss')
plt.legend(loc='upper right')
plt.xlabel('Epochs')
plt.ylabel('Loss, [mse]')
plt.ylim([0,.1])
plt.show()
# 查看训练集还原的误差分布如何,以便制定正常的误差分布范围
X_pred = model.predict(np.array(X_train))
X_pred = pd.DataFrame(X_pred,
columns=X_train.columns)
X_pred.index = X_train.index
scored = pd.DataFrame(index=X_train.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_train), axis = 1)
plt.figure()
sns.distplot(scored['Loss_mae'],
bins = 10,
kde= True,
color = 'blue')
plt.xlim([0.0,.5])
# 误差阈值比对,找出异常值
X_pred = model.predict(np.array(X_test))
X_pred = pd.DataFrame(X_pred,
columns=X_test.columns)
X_pred.index = X_test.index
threshod = 0.3
scored = pd.DataFrame(index=X_test.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_test), axis = 1)
scored['Threshold'] = threshod
scored['Anomaly'] = scored['Loss_mae'] > scored['Threshold']
scored.head()
七、基于分类的方法
1、One-Class SVM
One-Class SVM,这个算法的思路非常简单,就是寻找一个超平面将样本中的正例圈出来,预测就是用这个超平面做决策,在圈内的样本就认为是正样本,在圈外的样本是负样本,用在异常检测中,负样本可看作异常样本。它属于无监督学习,所以不需要标签。
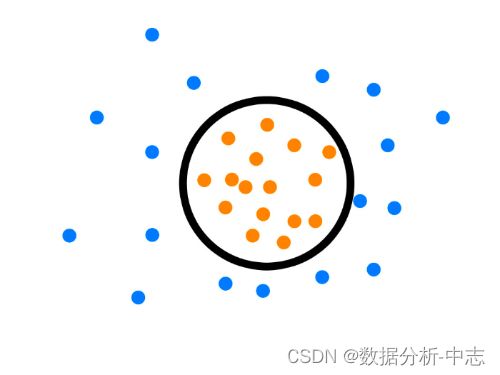
One-Class SVM又一种推导方式是SVDD(Support Vector Domain Description,支持向量域描述),对于SVDD来说,我们期望所有不是异常的样本都是正类别,同时它采用一个超球体,而不是一个超平面来做划分,该算法在特征空间中获得数据周围的球形边界,期望最小化这个超球体的体积,从而最小化异常点数据的影响。
假设产生的超球体参数为中心 o 和对应的超球体半径r>0,超球体体积V®被最小化,中心o是支持行了的线性组合;跟传统SVM方法相似,可以要求所有训练数据点xi到中心的距离严格小于r。但是同时构造一个惩罚系数为C的松弛变量 ζi,优化问题入下所示:
C是调节松弛变量的影响大小,说的通俗一点就是,给那些需要松弛的数据点多少松弛空间,如果C比较小,会给离群点较大的弹性,使得它们可以不被包含进超球体。
from sklearn import svm
# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel='rbf', gamma=0.1)
clf.fit(X)
y_pred = clf.predict(X)
n_error_outlier = y_pred[y_pred == -1].size
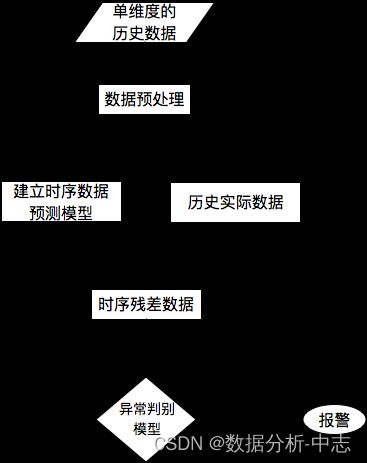
八、基于预测的方法
对于单条时序数据,根据其预测出来的时序曲线和真实的数据相比,求出每个点的残差,并对残差序列建模,利用KSigma或者分位数等方法便可以进行异常检测。具体的流程如下: