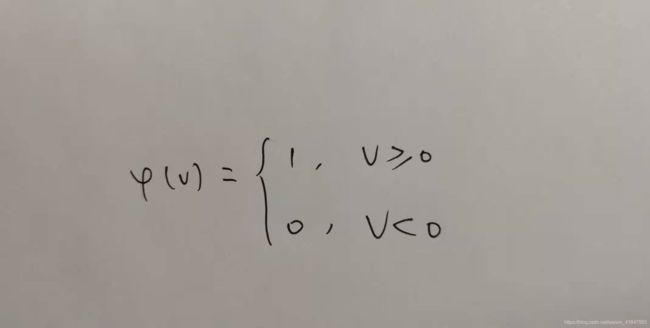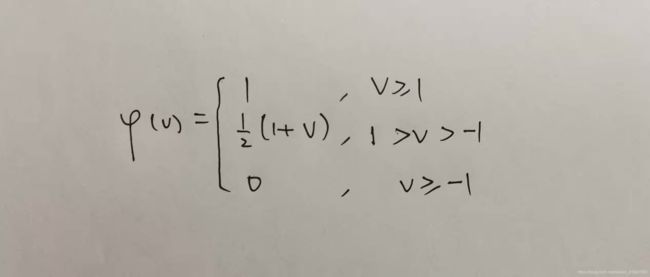基于BP神经网络的PID自适应控制——simulink平台(详细分析过程+完整代码+仿真结果)(一)
基于BP神经网络得PID自适应控制——simulink平台(详细分析过程+完整代码+仿真结果)(一)
- 一、神经网络简介和人工神经元模型
-
- 1. 连接权(突触权值)
- 2. 求和单元(加法器)
- 3. 激活函数(非线性)
-
- (1) 阈值激活函数
- (2) 分段线性激活函数
- (3) sigmoid激活函数
- (4) 双曲正切函数
- 二、神经网络的学习规则
-
- 1. 误差纠正学习规则
- 2. Hebb学习规则
- 3.竞争学习规则
一、神经网络简介和人工神经元模型
人生神经网络是模仿生物神经网络功能得一种验证模型。生物神经元受到传入的刺激,其反应又从输出端传到相连的神经元,输入与输出之间的关系一般是非线性的。神经网络是有大量的处理单元(神经元)互相连接而成的网络。为了模拟大脑的基本特性,在神经科学研究的基础上,提出了神经网络的模型。时间上,神经网络并没有完全反应大脑的功能,只是对生物神经网络进行了某种抽象、简化和模拟。
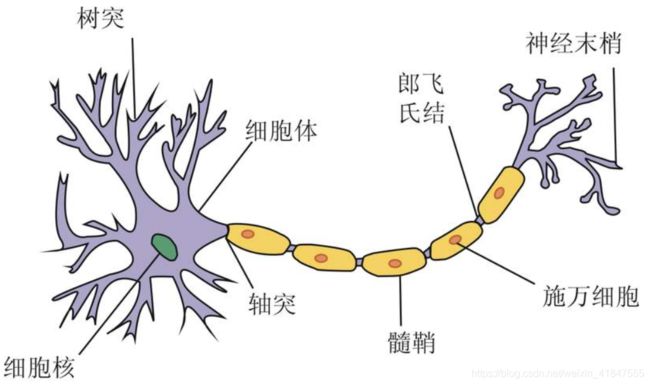
人工神经网络的基本单元是神经元模型,其主要包括三个基本要素:
1. 连接权(突触权值)
一组连接(对应于生物神经元的突触),连接强度由各连接上的权值表示,权值为正表示激活,为负表示抑制。
2. 求和单元(加法器)
一个求和单元,用于求取各输入信号的加权和(线性组合)。
3. 激活函数(非线性)
一个非线性激活函数,起到分线性映射作用,并将神经元输出幅值限制在一定范围内(一般限制在(0,1)或(-1,1)之间)。
此外,还有一个阈值 θ k \theta_{k} θk(或者偏置 b k = − θ k b_{k}=-\theta_{k} bk=−θk)。
以上作用可分别用数学式表达出来:
u k = ∑ j = 1 p w k j x j = w k 1 x 1 + w k 2 x 2 + ⋯ + w k p x p v k = u k − θ k , y k = φ ( v k ) \\ u_{k} = \sum_{j = 1}^{p} w_{kj}x_{j}= w_{k1}x_{1} + w_{k2}x_{2} + \dots+w_{kp}x_{p} \\ v_{k} = u_{k} - \theta_{k}, y_{k} = \varphi(v_{k} ) uk=j=1∑pwkjxj=wk1x1+wk2x2+⋯+wkpxpvk=uk−θk,yk=φ(vk)
其中, x 1 , x 2 , … , x p x_{1}, x_{2}, \dots, x_{p} x1,x2,…,xp为输入信号, w k 1 , w k 2 , … , w k p w_{k1},w_{k2},\dots,w_{kp} wk1,wk2,…,wkp为神经元 k k k之权值, u k u_{k} uk为线性组合结果, θ k \theta_{k} θk为阈值, φ ( ⋅ ) \varphi(·) φ(⋅)为激活函数, y k y_{k} yk为神经元的输出。
偏置 b k b_{k} bk是神经元 k k k的外部参数,我们可以像处理输入信号一样考虑它,因而得到神经元模型的另一种描述图,如下。
对应上图的数学描述为
v k = ∑ j = 0 p w k j x j = w k 0 x 0 + w k 1 x 1 + w k 2 x 2 + ⋯ + w k p x p \\ v_{k} = \sum_{j = 0}^{p} w_{kj}x_{j}= w_{k0}x_{0}+w_{k1}x_{1} + w_{k2}x_{2} + \dots+w_{kp}x_{p} vk=j=0∑pwkjxj=wk0x0+wk1x1+wk2x2+⋯+wkpxp
其中 x 0 = + 1 ( 或 − 1 ) x_{0}=+1(或-1) x0=+1(或−1),权值 w k 0 = θ k w_{k0}=\theta_{k} wk0=θk
(1) 阈值激活函数
(2) 分段线性激活函数
(3) sigmoid激活函数
sigmoid激活函数即为S型函数。
φ ( v ) = 1 1 + e x p ( − α v ) \varphi(v) = \frac{1}{1+exp(-\alpha v)} φ(v)=1+exp(−αv)1
其中 α > 0 \alpha > 0 α>0可控制斜率。
(4) 双曲正切函数
φ ( v ) = t a n h ( v 2 ) = 1 − e x p ( − v ) 1 + e x p ( − v ) \varphi(v) = tanh(\frac{v}{2})=\frac{1-exp(-v)}{1+exp(-v)} φ(v)=tanh(2v)=1+exp(−v)1−exp(−v)
此函数具有平滑和渐进性,并保持单调性。
二、神经网络的学习规则
通常用到的学习规则有三种。
1. 误差纠正学习规则
在这里,我们令 y k ( n ) y_{k}(n) yk(n)是输入 x k ( n ) x_{k}(n) xk(n)时神经元 k k k在n时刻的实际输出, d k ( n ) d_{k}(n) dk(n)表示期望的输出,则误差信号可写为
e k ( n ) = d k ( n ) − y k ( n ) e_{k}(n) = d_{k}(n)-y_{k}(n) ek(n)=dk(n)−yk(n)
最终目的:使某一基于 e k ( n ) e_{k}(n) ek(n)的目标函数达到要求,以使网络中每一输出单元的实际输出在某种意义上逼近应有输出。学习过程是将误差信号 e k ( n ) e_{k}(n) ek(n)作用于神经元k的突出权值修正调节中,以一步步逼近的方式使输出信号 y k ( n ) y_{k}(n) yk(n)向期望 d k ( n ) d_{k}(n) dk(n)靠近。一旦选定了目标函数形式,误差纠正学习就变成了一个典型的优化问题。最常用的目标函数是均方差判据,定义为误差平方和的均值:
J = E [ 1 2 ∑ k e k 2 ( n ) ] J =E \left[ \frac{1}{2} \sum_{k}^{} e_{k}^{2}(n) \right] J=E[21k∑ek2(n)]
E为期望算子。上式的前提是被学习的过程是平稳的,具体方法科用最优梯度下降法。直接用J作为目标函数时需要知道整个过程的统计特性,为解决这一问题,通常用 J J J在时刻n的瞬时值代替 J J J,即
E = 1 2 ∑ k e k 2 ( n ) E = \frac{1}{2} \sum_{k}^{} e_{k}^{2}(n) E=21k∑ek2(n)
问题变成求 E E E对权值 w w w的极小值,按梯度下降法,可得
Δ w k j ( n ) = − η ∂ ε ( n ) ∂ w k j ( n ) = η ( − ∂ ε ( n ) ∂ v k ( n ) ) ∂ v k ( n ) ∂ w k j ( n ) = η e k ( n ) φ ′ ( v k ( n ) ) x j ( n ) \Delta w_{kj}(n) = -\eta \frac{\partial \varepsilon (n)}{\partial w_{kj}(n)}=\eta \left( -\frac{\partial \varepsilon (n)}{\partial v_{k}(n)} \right) \frac{\partial v_{k}(n)}{\partial w_{kj}(n)}=\eta e_{k}(n)\varphi^{'}(v_{k}(n)) x_{j}(n) Δwkj(n)=−η∂wkj(n)∂ε(n)=η(−∂vk(n)∂ε(n))∂wkj(n)∂vk(n)=ηek(n)φ′(vk(n))xj(n)
式中, η \eta η为学习步长,这就是所说的误差纠正学习规则。
突触权值的更新可按下式来确定
w k j ( n + 1 ) = w k j ( n ) + Δ w k j ( n ) w_{kj}(n+1) = w_{kj}(n) + \Delta w_{kj}(n) wkj(n+1)=wkj(n)+Δwkj(n)
2. Hebb学习规则
由神经心理学家Hebb提出,可归纳为“如果在某一突触(连接)每一边的两个神经元被同步激活,(同为激活或同为抑制),那么突触的强度被选择性地增强,反之则被选择性地减弱”,其数学描述为
Δ w k j ( n ) = w k j ( n + 1 ) − w k j ( n ) = η y k ( n ) x j ( n ) \Delta w_{kj}(n)=w_{kj}(n+1) - w_{kj}(n)=\eta y_{k}(n)x_{j}(n) Δwkj(n)=wkj(n+1)−wkj(n)=ηyk(n)xj(n)

(唐纳德·赫布(Donald Olding Hebb,1904.07.22-1985.08.20),加拿大心理学家,认知心理生理学的开创者。出生于加拿大新斯科舍省的切斯特(Chester Basin),逝于加拿大新斯科舍省。)
3.竞争学习规则
在竞争学习时,网络各输出单元相互竞争,最后只有一个最强者被激活。
一篇写不完,转到下一篇继续写基于BP神经网络得PID自适应控制——simulink平台(详细分析过程+完整代码+仿真结果)(二)。