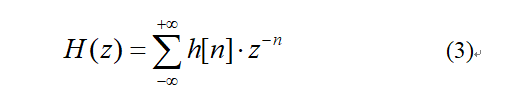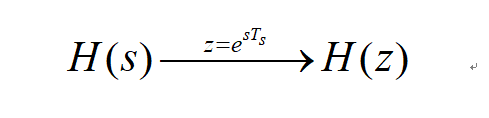IIR滤波器设计之冲激响应不变法与双线性变换法
前言
IIR(Infinite Impulse Response)数字滤波器是指无限长冲激响应数字滤波器,因其具有良好的幅频响应特性,被广泛应用于通信、控制、生物医学、振动分析、雷达和声呐等领域。
IIR滤波器的设计可以通过设计一个模拟滤波器,进而利用冲激响应不变法或者双线性变换法来进行数字滤波器的设计。
注意:本博文中部分图片来源于慕课视频的截图,课程是北京航空航天大学的数字信号处理。
一、冲激响应不变法
h[n]与h(t)之间的关系可根据采样过程推导,如图1所示:
对式(1)做拉普拉斯变换得:
h[n]的Z变换为:
对比式(2)和式(3)可知,H(s)与H(z)的转换关系为:
w与Ω的转换关系为:
二、双线性变换法
双线性变换即经过了两次线性变换,第一次是将Ω从正无穷大变换到π/T,负无穷大变换到-π/T;第二次是将S域的左半平面映射到Z域的单位圆内。 双线性变换过程如图2所示。
H(s)与H(z)的转换关系为:
w与Ω的转换关系为:
三、MATLAB代码
%% 冲击响应不变法设计巴特沃斯数字低通滤波器
T = 2; % 设置采样周期
fs = 1/T; % 采样频率
Wp = 0.30 * pi/T; % 设置归一化通带和阻带截止频率
Ws = 0.35 * pi/T;
Ap = 20 * log10(1/0.8); % 设置通带最大衰减和阻带最小衰减
As = 20 * log10(1/0.18);
% 调用buttord函数确定巴特沃斯滤波器阶数
[N ,Wc] = buttord(Wp,Ws,Ap,As,'s');
% 调用butter函数设计巴特沃斯滤波器
[B ,A] = butter(N,Wc,'s');
W = linspace(0,pi,400*pi); % 指定一段频率值
% 计算模拟滤波器的幅频响应
Hs = freqs(B,A,W);
% 调用冲击响应不变法
[Bz,Az] = impinvar(B,A,fs);
% 返回频率响应
Hz = freqz(Bz,Az,W);
%% 画图
figure;
subplot(1,2,1);
plot(W/pi,abs(Hs)/abs(Hs(1))); % 绘制巴特沃斯模拟滤波器的幅频特性曲线
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯模拟滤波器');grid on;
subplot(1,2,2);
plot(W/pi,abs(Hz)/abs(Hz(1))); % 绘制巴特沃斯数字低通滤波器的幅频特性曲线
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯数字滤波器');grid on;%% 双线性变换法设计巴特沃斯数字带阻滤波器
T = 2; % 设置采样周期
fs = 1/T; % 采样频率
wp = [0.30*pi,0.75*pi];
ws = [0.35*pi,0.65*pi];
Wp = (2/T)*tan(wp/2); % 设置归一化通带和阻带截止频率
Ws = (2/T)*tan(ws/2);
Ap = 20 * log10(1/0.8); % 设置通带最大衰减和阻带最小衰减
As = 20 * log10(1/0.18);
% 调用buttord函数确定巴特沃斯滤波器阶数
[N ,Wc] = buttord(Wp,Ws,Ap,As,'s');
% 调用butter函数设计巴特沃斯滤波器
[B ,A] = butter(N,Wc,'stop','s');
W = linspace(0,pi,400*pi); % 指定一段频率值
% 计算模拟滤波器的幅频响应
Hs = freqs(B,A,W);
% 调用双线性变换法
[Bz,Az] = bilinear(B,A,fs);
% 返回频率响应
Hz = freqz(Bz,Az,W);
%% 画图
figure;
subplot(1,2,1);
plot(W/pi,abs(Hs)); % 绘制巴特沃斯模拟滤波器的幅频特性曲线
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯模拟滤波器');grid on;
subplot(1,2,2);
plot(W/pi,abs(Hz)); % 绘制巴特沃斯数字带阻滤波器的幅频特性曲线
xlabel('频率/Hz');ylabel('幅值');title('巴特沃斯数字滤波器');grid on;总结
冲激响应不变法的优缺点
优点:1)完全模仿模拟滤波器的单位冲激响应,即时域逼近良好;2)线性相位的模拟滤波器通过冲激响应不变法得到的仍为线性相位的数字滤波器。
缺点:频率响应的混叠效应。
双线性变换法的优缺点
优点:避免了频率响应的混叠效应。
缺点:1)不再保持原有的线性相位,呈分段常数型;2)各个分段边缘的临界频率点产生了畸变。
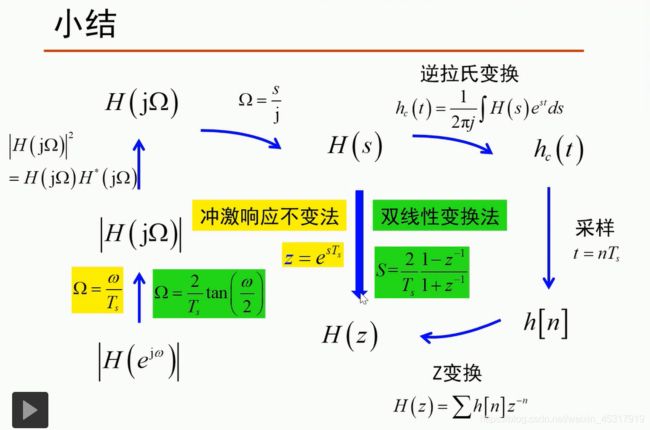
首先,根据待设计数字滤波器的幅频响应,转换为模拟滤波器的幅频响应,然后找到一个连续系统滤波器的频率响应H(jΩ)满足待设计数字滤波器的幅频响应,进而找到满足该幅频响应的连续系统的系统函数H(s),根据推导得到的H(s)与H(z)的转换表达式,得到H(z),即离散系统的系统函数。