机器学习--逻辑斯谛回归（Logistic Regression）

机器学习–逻辑斯谛回归（Logistic Regression）

基本概念

逻辑斯谛回归（Logistic Regression）虽然带回归，却是经典的分类方法。逻辑斯谛回归模型属于对数线性模型。它在线性模型的基础上，使用 Sigmoid 函数，将线性模型的结果映射到 [0, 1] 之间，实现了具体值到概率的转换。

线性回归：
$$f(x)=w^{T}x+b$$
Sigmoid：
$$S(x)=\frac{1}{1+e^{-x}}$$
l逻辑斯谛回归：
$$f(x)=S(w^{T}x)=\frac{1}{1+e^{-w^{T}x+b}}$$

逻辑斯谛分布

设 $X$ 是连续随机变量，当 $X$ 服从逻辑斯谛分布时，$X$ 的分布函数和密度函数可以表示为（《统计机器学习》）：
$$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu )/\gamma }}$$
$$f(x)=F^{{}^{\prime }}(x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/\gamma }{)}^2}$$
其中，$\mu$ 为位置参数，$\gamma >0$ 为形状参数。

二项逻辑斯谛回归

二项逻辑斯谛回归模型（binomial logistic regression model）是一种分类模型。并且分类结果只有0和1两种。
$$P(Y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$
$$P(Y=0|x)=\frac{1}{1+e^{w^{T}x+b}}$$
在求得两个概率之后，逻辑斯谛回归模型比较这两个条件概率值的大小，将实例 $x$ 分到概率值较大的那一类。

逻辑斯谛回归模型的特点：一个事件的几率是指该事件发生的概率与该时间不发生的概率的比值。对于逻辑斯谛回归而言，$P(Y=1|x)$ 发生的对数几率是：
$$log\frac{P(Y=1|x)}{1-P(Y=1|x)}=w^{T}x+b$$
这表明，在逻辑斯谛回归模型中，输出 Y = 1 的对数几率是输入 $x$ 的线性函数。另一种说法是，输出 Y = 1 的对数几率是由输入的线性函数表示的模型，即逻辑斯谛回归模型。

代价函数

如果我们使用线性回归中的代价函数进行梯度下降法计算，有可能得到局部最优解，无法求得最优的参数值，因此我们使用极大似然估计 求得代价函数。

我们以二分类为例（二项逻辑斯谛回归）。
令:
$$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$$
可以得到似然函数为：
$$\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}$$
取对数
$$\begin{gathered} L(w)=\sum _{i=1}^N[y_{i}log\pi (x_i)+(1-y_i)log(1-\pi (x_i))] \\ =\sum _{i=1}^N[y_{i}log\frac{\pi (x_i)}{1-\pi (x_i)}+log(1-\pi (x_i))] \\ =\sum _{i=1}^N[y_i(w^T{x}_i+b)-log(1+e^{w^T{x}_i+b})] \end{gathered}$$
对 $L(w)$ 求极大值，得到 $w$ 的估计值。

令代价函数为
$$J(w)=-L(w)$$
接下来用梯度下降法或牛顿法来求解参数。我们先求出偏导数 $\frac{\partial J(w)}{\partial w}$ 和 $\frac{\partial J(w)}{\partial b}$:
$$\frac{\partial J(w)}{\partial w}=\frac{1}{N}{x}_i(w^T{x}_i+b-y_i)$$
$$\frac{\partial J(w)}{\partial b}=\frac{1}{N}\sum _{i=1}^N(w^T{x}_i+b-y_i)$$

在求得偏导数之后，我们对参数进行迭代更新

$$w=w-lr\ast \frac{\partial J(w)}{\partial w}$$
$$b=b-lr\ast \frac{\partial J(w)}{\partial b}$$

经过多次迭代后，我们的模型能学习到一个很好的参数。

实例

# coding=utf-8
from sklearn.datasets import make_classification
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

def load_data():

    X, y = make_classification(n_samples=10000, n_features=10, n_redundant=3, n_informative=3, n_classes=2,
                               n_clusters_per_class=1, random_state=42)
    return X, y


class LogisticRegression:
    def __init__(self, lr=0.01, epoch=1000):

        # 学习率
        self.lr = lr

        # 迭代次数
        self.epochNum = epoch

        self.train_loss = []

    # 定义 sigmoid 函数
    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

    # 用来计算梯度 dw 和 db
    def gradient(self, X, y):
        h = self.sigmoid(np.dot(X, self.w) + self.b)
        dw = np.dot(X.T, (h - y)) / X.shape[0]
        db = np.sum(h - y) / X.shape[0]
        return dw, db

    # 计算损失
    def loss(self, X, y):
        m = len(y)
        h = self.sigmoid(np.dot(X, self.w) + self.b)

        # 参考公式
        cost = (-1 / m) * (np.dot(y.T, np.log(h)) + np.dot((1 - y).T, np.log(1 - h)))
        cost = cost.squeeze()

        # 带有 L2 正则化项
        reg = (self.lr / 2) * np.sum(np.dot(self.w.T, self.w))

        return cost + reg

    # 拟合函数
    def fit(self, X, y):
        # 输入要为二维，将标签增维
        y = y.reshape(-1, 1)

        # 初始化参数 w 和 b
        self.w = np.zeros((X.shape[1], 1))
        self.b = np.zeros((X.shape[0], 1))

        for epoch in range(self.epochNum):

            # 计算损失和梯度
            loss = self.loss(X, y)
            dw, db = self.gradient(X,  y)

            # 更新参数 w 和 b
            self.w = self.w - self.lr * dw
            self.b = self.b - self.lr * db
            self.train_loss.append(loss)

    def show_parameters(self):
        print('w:', self.w)

    def predict(self, x_test):
        prediction =self.sigmoid(np.dot(x_test, self.w))
        prediction = prediction > 0.5
        prediction = prediction.astype(int)
        return prediction

    # 绘图
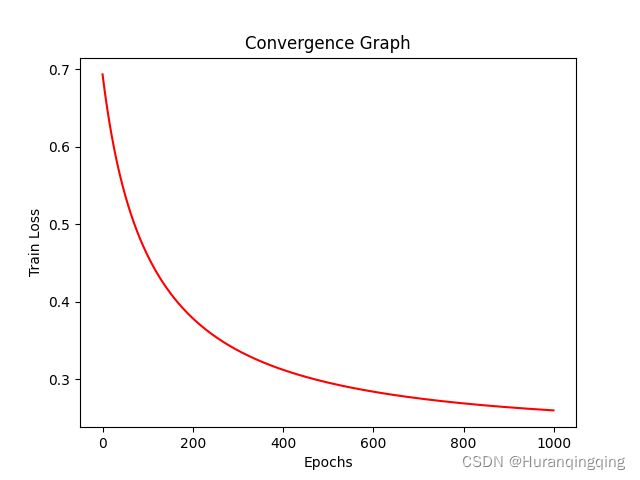
    def plot_loss(self):
        plt.figure()
        plt.plot(range(len(self.train_loss)), self.train_loss, 'r')
        plt.title("Convergence Graph")
        plt.xlabel("Epochs")
        plt.ylabel("Train Loss")
        plt.show()


if __name__ == '__main__':

    X, y = load_data()

    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

    model = LogisticRegression()
    model.fit(x_train, y_train)
    model.plot_loss()
    pre = model.predict(x_test)
    acc = accuracy_score(y_test, pre)
    print(acc)