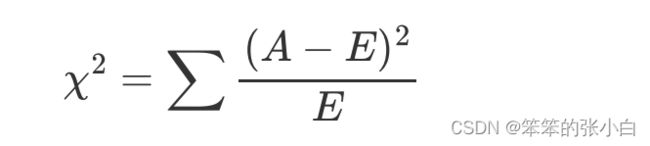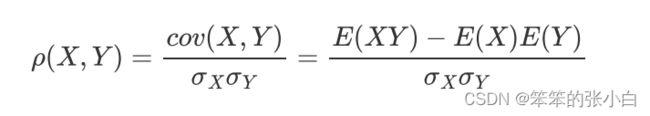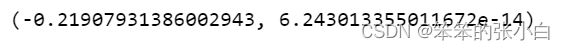Python实现卡方检验和相关性分析
目录
卡方检验
卡方检验的statsmodels实现
配对卡方检验
相关分析(关联性分析)概述
相关系数的计算原理
相关分析的Python实现
卡方检验
卡方检验的主要用途
- 两个率或两个构成比比较的卡方检验
- 多个率或多个构成比比较的卡方检验
- 分类资料的相关分析
卡方检验的基本原理
H0 :观察频数与期望频数没有差别
其原理为考察基于H0的理论频数分布和实际频数分布间的差异大 小,据此求出相应的P值
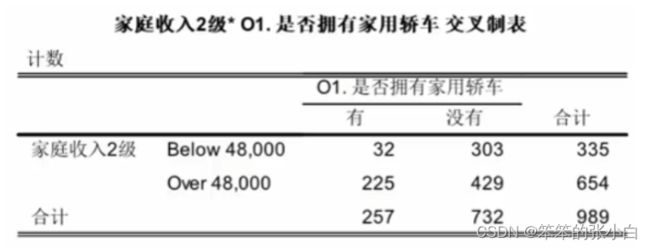
案例: 所有受访家庭会按照家庭年收入被分为低收入家庭和高收入家 庭两类,现希望考察不同收入级别的家庭其轿车拥有率是否相同。
基于H0成立,即观察频数和期望频数无差别,也就是两组变量 (家庭收入级别与是否拥有轿车)相互不产生影响,两组变量不相 关,如果检验P值很高,则接受H0;如果检验P值很低,则检验不通 过,观察频数和期望频数有差别,两组变量相关。
卡方统计量
卡方统计量的计算公式:
其中A为实际频数,E为期望频数(理论频数)。
卡方统计量的理解:
- 当观察频数与期望频数完全一致时,卡方值为0
- 观察频数与期望频数越接近,两者之间的差异越小,卡方值越小
- 观察频数与期望频数差异越大,卡方值越大
- 卡方值的大小也和自由度有关
卡方检验的statsmodels实现
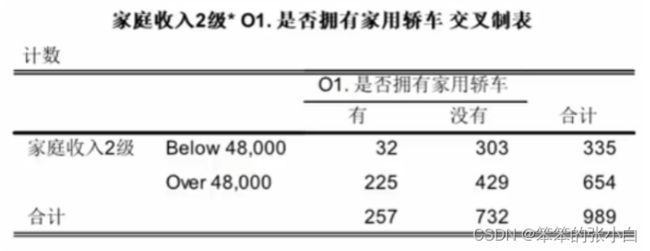
案例: 所有受访家庭会按照家庭年收入被分为低收入家庭和高收入家 庭两类,现希望考察不同收入级别的家庭其轿车拥有率是否相同。
statsmodels中首先需要建立对应的列联表对象:
Table类的方法: test_nominal_association() 无序分类行、列变量的独立性检验
import pandas as pd
import statsmodels.stats.contingency_tables as tbl
# 读取excel文件
home = pd.read_excel("home_income.xlsx")
# 考察不同收入级别的家庭其轿车拥有率是否相同
table = tbl.Table(pd.crosstab(home.Ts9,home.O1))
res = table.test_nominal_association() # 卡方检验
print("卡方值:",res.statistic)
print("自由度:",res.df)
print("p值:",res.pvalue) # 格式化后的p值配对卡方检验
McNemar's检验(配对卡方检验)用于分析两个相关率的变化是否 有统计学意义
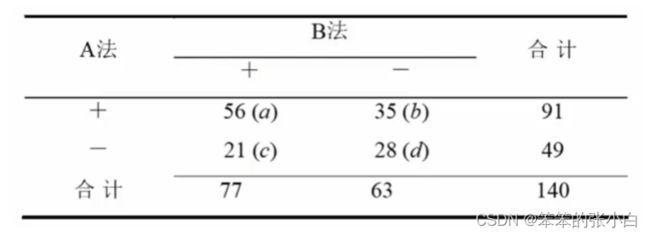
案例: 用A、B两种方法检查已确诊的某种疾病患者140名,A法检出91 名(65%),B法检出77名(55%),A、B两法一致的检出56名(40%), 问哪种方法阳性检出率更高?
分析思路:
- H0 :两种方法阳性检出率无差别,即b单元格=c单元格
- 对同一个体,分别有两次不同的测量,并最终构成了两组数据, 因此研究框架是自身配对设计
- 求出各对的差值,然后考察样本中差值的分布是否按照H0假设 的情况对称分布
- 主对角线上的样本,两种检验方法的结论相同
- 非主对角线上的单元格才携带检验方法的差异信息
- 根据H0得到b、c两格的理论数均为(b+c)/2,对应的配对检验统计 量,经过化简后是:
一般在 b + c < 40 时,需用确切概率法进行检验,或者进行校正
代码实现
statsmodels.stats.contingency_tables中常用的配对卡方的分析使用:
- 1 tbl.SquareTable 用于分析行列变量类别相同的对称结构方表 (近似结果)
- 2 tbl.mcnemar 用于分析配对四格表(确切概率结果)
用SquareTable类分析
import numpy as np
import statsmodels.stats.contingency_tables as tbl
table = tbl.SquareTable(np.array([[56,35],[21,28]]))
print(table.summary()) # 查看汇总结果
print(table.symmetry()) # 只查看配对卡方检验的结果用mcnemar类分析
table = tbl.mcnemar(pd.DataFrame([[56,35],[21,28]]))
table.pvalue # 确切概率结果相关分析(关联性分析)概述
什么是相关分析(关联性分析)
相关分析是用于考察变量间数量关系密切程度的分析方法,例如: 身高与体重的关系。
几乎所有涉及到多个变量的假设检验方法,都可以被看作是这些变 量间的关联性分析。
- t检验:分组变量与连续因变量间的关联性分析
- 卡方检验:行、列分类变量间的关联性分析
- 聚类分析:案例(case)间的关联性分析
- 多变量回归:因变量和一组自变量间的关联性分析
各种相关系数
- 连续 vs 连续:Pearson相关系数(双变量正态分布); Spearman秩相关系数(不符合双变量正态分布)
- 有序 vs 有序:Gamma系数、肯德尔相关系数等(例如:医生 级别与治疗效果的相关关系);也可使用Spearman秩相关系数
- 无序 vs 无序:列联系数等(例如:民族与职业的关系)
- 基于卡方统计量进一步推导而来
- 无方向 0~1
- OR/RR:一类特殊的关联强度指标
- 连续 vs 分类:Eta(本质上是方差解释度,即连续变量的离散度 有多少可以被另外的分类指标所解释)
统计图/统计表在相关分析中的重要性
- 连续变量:用散点图先确认关联趋势是否为直线
- 分类变量:分组条图、马赛克图(分组百分条图)等工具
相关系数的计算原理
常用术语(针对两连续变量的相关)
- 直线相关:两变量呈线性共同增大,或者呈线性一增一减的情况
- 曲线相关:两变量存在相关趋势,但是为各种可能的曲线趋势
- 正相关与负相关:如果A变量增加时B变量也增加,则为正相 关,如果A变量增加时B变量减小,则为负相关
- 完全相关:完全正相关;完全负相关
- 零相关:自变量的变化,不会影响因变量的变化
Pearson相关系数
- 计算公式
公式理解:标准差代表变量的离散程度(信息量大小); 协方差Cov(X,Y)代表各变量共同携带的信息量大 小; 相关系数代表两个变量总信息量中的共同部分占比。
- 相关系数ρ的取值范围:-1 < ρ < 1
- 其正负反映了相关的方向
- |ρ|越接近于1,说明相关性越好
- |ρ|越接近于0,说明相关性越差
- Pearson相关系数的检验:
- H0 :两变量间无直线相关关系,ρ=0
- 检验方法:t检验
- Pearson相关系数的适用条件:
- 必须是线性相关的情形(可以先绘制散点图观察一下)
- 针对两连续变量的相关系数
- 极端值对相关系数的计算影响极大,因此要慎重考虑和使用
- 要求相应的变量呈双变量正态分布(近似也可以)
Spearman秩相关系数
- 不服从正态分布的变量、分类或等级变量之间的关联性可采用
- Spearman秩相关系数 Spearman提出首先对数据做秩变换,然后再计算两组秩间的直 线相关系数(秩变换分析思想)
相关分析的Python实现
相关分析作为比较简单的方法,在statsmodels中并未作进一步 的完善,因此主要使用scipy实现。
- 两个连续变量,且符合双变量正态分布:Pearson相关系数
scipy.stats.pearsonr(a, b)- 两个连续变量,不符合双变量正态分布:Spearman秩相关系数
scipy.stats.spearmanr(a, b)- 两个有序变量:Kendall's Tau;Spearman秩相关系数
scipy.stats.kendalltau(a, b) # 肯德尔相关系数
scipy.stats.spearmanr(a, b) # 斯皮尔曼秩相关系数import pandas as pd
from scipy import stats as ss
home = pd.read_excel("home_income.xlsx") # 读取excel文件
# 考察年龄(s3)与总信心指数(index1)间的相关关系
# 先通过散点图,观察两个变量是否为线性关系
home.plot.scatter("s3","index1")
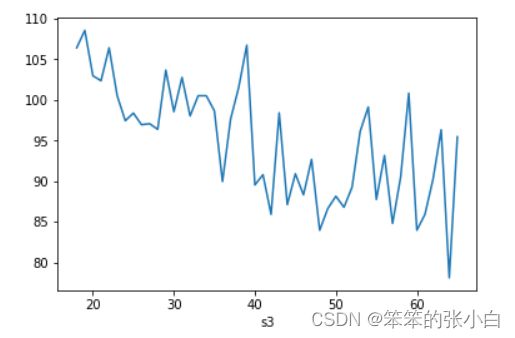
# 年龄分组,重新观察两个变量是否为线性关系
home.groupby("s3").index1.mean().plot()
# 返回皮尔逊相关系数和p值
ss.pearsonr(home.s3,home.index1)