leetcode(力扣) 452. 用最少数量的箭引爆气球 & 435. 无重叠区间 & 56. 合并区间 (贪心)

这三道题都是重叠区间问题，放到一起做吧。

452. 用最少数量的箭引爆气球

题目描述

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。
给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1：
输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：
输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：
输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:

• 在x = 2处发射箭，击破气球[1,2]和[2,3]。
• 在x = 4处射出箭，击破气球[3,4]和[4,5]。

思路分析

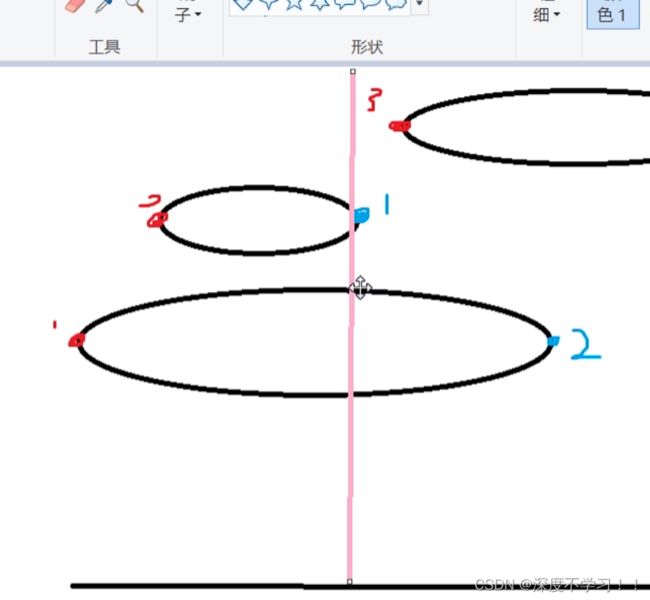
假设有下面两个这样的气球中间有一支箭。

设上面的小气球是A，下面的大气球是B。

显然我们要先考虑小的气球，因为考虑大的可能射不到小的，先考虑小的能射到大的。

如果A的右边界>=B的左边界，则射A右边界那个点一定能将B气球也射爆。

将题目所给的数组进行排序，当然，要按照右边界进行排序。

算法思路：

记录第一个值的右边界，不断遍历后续的值的左边界，如果后续的左边界都小于刚才记录的右边界，则表示 这些都值都有重叠区间，可以一箭射完。

如果出现左边界大于刚才记录的右边界时，则表示需要另一只箭了。此时重新记录新的右边界，继续往后遍历。

完整代码

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x:x[1])


        right_min = points[0][1]
        res = 1
        for i in range(len(points)):
            if points[i][0] > right_min:
                res+=1
                right_min = points[i][1]
        return res

435. 无重叠区间

和上面这道题的思路一样，甚至代码都不用怎么改。

这道题要找，使得数组中区间五重叠时要删除的最少区间数。

这道题里 [1,2] [2,3] 属于不同区间，这是和上一道题不一样的地方。(所以修改一下if语句 加个等号。)

直接用上面的代码求出来需要射多少箭，实际上等于有多少个不同的区间。

总共的区间数 - 不同的区间数 = 要删除的区间数。（修改返回值哪一行代码。）

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        intervals.sort(key=lambda x:x[1])
        points = intervals
        right_min = points[0][1]
        res = 1
        for i in range(len(points)):
            if points[i][0] >= right_min:
                res+=1
                right_min = points[i][1]
        return len(intervals)-res

56. 合并区间

这三道题思路一样。

首先排序，按照第一个元素排序。

设变量 left 记录首位元素第一个元素的值 即 [0][0]，right记录首位元素第二个元素的值即[0][1]。res为收集答案数组。

遍历所给数组，

• 若发现区间的左边界小于等于此时记录的最大右边界，则这个区间是可以和前面合并的，此时更新最大右边界，这是这道题和上面两道不一样的地方。

• 若发现区间左边界大于此时记录的最大右边界，则这个区间是无法合并的，这时将记录的left和right加入到res答案数据集，然后更新left和right为当前遍历的区间左右端点，继续下轮遍历。

有一个细节，就是按照这个方法，会处理不到最后一个数组。

比如 [[1,3],[2,6],[8,10],[15,18]]， 遍历到第四个区间的时候，left为8 right为10。

此时的15大于记录的right =10。所以将区间[8,10]加入了答案数组，更新了left=15，right=18.然后遍历结束了，会发现没处理最后一个区间，所以最后单独处理一下就行了。

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key= lambda  x:x[0])
        print(intervals)

        left = intervals[0][0]
        right = intervals[0][1]
        res = []
        for i in range(1,len(intervals)):
            if intervals[i][0] <= right: # 可合并区间
                right = max(right,intervals[i][1])
            else:
                res.append([left,right])
                left = intervals[i][0]
                right = intervals[i][1]
        res.append([left,right])   # 单独处理
        print(res)
        return res