(六) 三维点云课程---FPFH特征点描述
三维点云课程—FPFH特征点描述
三维点云课程---FPFH特征点描述
- 三维点云课程---FPFH特征点描述
-
- 1.FPFH推导
-
- 1.1PFH介绍 (Point Feature Histogram)
- 1.2FPFH介绍 (Fast Point Feature Histogram)
- 2.FPFH完整代码即仿真效果
1.FPFH推导
1.1PFH介绍 (Point Feature Histogram)
讲解FPFH之前,先来简单介绍一下PFH的理论。
PFH算法的输入是:三维点云数据,每个点的表面法向量以及特征点,输出是一个 B 3 B^3 B3长度的数组,其中 B B B是每个直方图的个数,至于为什么是 B 3 B^3 B3,请往下看。pfh是基于直方图的方法进行特征点描述的,以特征点为圆心,通过投票的方式进行描述,如上图所示。那么pfh的描述方法是什么呢?

其中 n 1 n_1 n1表示 p 1 p_1 p1表面的法向量, n 2 n_2 n2表示 p 2 p_2 p2表面的法向量
u = n 1 v = u × p 2 − p 1 ∣ ∣ p 2 − p 1 ∣ ∣ 2 w = u × v u=n_1\\ v=u \times \frac {p_2-p_1}{||p_2-p_1||_2}\\ w=u \times v u=n1v=u×∣∣p2−p1∣∣2p2−p1w=u×v
在PFH中以 [ α , ϕ , θ , d ] [\alpha,\phi ,\theta ,d] [α,ϕ,θ,d]作为描述,其中
d = ∣ ∣ p 2 − p 1 ∣ ∣ 2 α = v ⋅ n 2 ϕ = u ⋅ p 2 − p 1 ∣ ∣ p 2 − P 1 ∣ ∣ 2 θ = a r c t a n ( w ⋅ n 2 , u ⋅ n 2 ) d=||p_2-p_1||_2\\ \alpha=v \cdot n_2\\ \phi=u \cdot \frac{p_2-p_1}{||p_2-P_1||_2}\\ \theta=arctan(w \cdot n_2,u \cdot n_2) d=∣∣p2−p1∣∣2α=v⋅n2ϕ=u⋅∣∣p2−P1∣∣2p2−p1θ=arctan(w⋅n2,u⋅n2)
其中注意在计算 θ \theta θ的时候, n 2 n_2 n2在 w w w上的投影是 n 2 ⋅ w ∣ ∣ w ∣ ∣ 2 \frac{n_2 \cdot w}{||w||_2} ∣∣w∣∣2n2⋅w, n 2 n_2 n2在 u u u上的投影为 n 2 ⋅ u ∣ ∣ u ∣ ∣ 2 \frac{n_2 \cdot u}{||u||_2} ∣∣u∣∣2n2⋅u,并且 u , v , w u,v,w u,v,w均为单位向量。注意其实在实际PFH应用中,我们舍弃 d d d这个描述信息,因为对于点云来说,距离激光雷达或者RGBD传感器较近的地方,点云比较密集, d d d相比较小,而距传感器较远的地方,点云比较稀疏, d d d相比较大。而对于一个物体来说,不管远的部分还是近的部分,都表示该物体。所以对于PFH的特征描述为 [ α , ϕ , θ ] [\alpha,\phi,\theta] [α,ϕ,θ]。

上图是PFH其中一个特征点与其r领域内的连接关系,显然特征点和领居之间是全连接的。假设在 r r r领域内有 k k k个点,那么PFH有 k 2 k^2 k2的三元组。其次PFH的作者在实现该方法时,是将 k 2 k^2 k2个三元组映射到直方图中,并将 [ α , ϕ , θ ] [\alpha,\phi,\theta] [α,ϕ,θ]作为三个轴,其中每一个维度有 B B B个,故PFH输出的是一个 B 3 B^3 B3长度的数组。算法复杂度为 O ( n k 2 ) O(nk^2) O(nk2),其中 n n n为点云个数, k k k为邻居个数。
1.2FPFH介绍 (Fast Point Feature Histogram)
SPFH不同于PFH的是,SPFH并不是全连接,每次只需要计算自身的特征点的描述子和其邻居的描述子,大大减少的计算量
- 输出为 3 B 3B 3B长度的描述变量,而不是 B 3 B^3 B3,简单来说
[ α 1 . . . α B ] ⏟ B + [ ϕ 1 . . . ϕ B ] ⏟ B + [ θ 1 . . . θ B ] ⏟ B \underbrace {\begin{bmatrix} {{\alpha _1}}&{...}&{{\alpha _B}} \end{bmatrix}}_B + \underbrace {\begin{bmatrix} {{\phi _1}}&{...}&{{\phi _B}} \end{bmatrix}}_B + \underbrace {\begin{bmatrix} {{\theta _1}}&{...}&{{\theta _B}} \end{bmatrix}}_B B [α1...αB]+B [ϕ1...ϕB]+B [θ1...θB]
那么FPFH的计算步骤为
1.计算自身特征点的SPFH描述子,记为 S P F H ( p q ) SPFH(p_q) SPFH(pq)
spfh_query = get_spfh(point_cloud, search_tree, keypoint_id, radius, B)
2.计算以特征点为圆心,以r为半径的圆内,各领居的SPFH描述子,记为 S P F H ( p k ) SPFH(p_k) SPFH(pk)
X = np.asarray([get_spfh(point_cloud, search_tree, i, radius, B) for i in idx_neighbors])
F P F H ( p q ) = S P F H ( p q ) + 1 k ∑ i = 1 k w k ⋅ S P F H ( p k ) w k = 1 ∣ ∣ p q − p k ∣ ∣ 2 FPFH(p_q)=SPFH(p_q)+\frac{1}{k}{\sum \limits_{i=1}^k{w_k \cdot SPFH(p_k)}}\\ w_k=\frac{1}{||p_q-p_k||_2} FPFH(pq)=SPFH(pq)+k1i=1∑kwk⋅SPFH(pk)wk=∣∣pq−pk∣∣21
算法复杂度为 O ( n k ) O(nk) O(nk)。
# neighborhood contribution:
spfh_neighborhood = 1.0 / (k - 1) * np.dot(w, X)
fpfh = spfh_query + spfh_neighborhood
4.归一化FPFH计算的值
# normalize again:
fpfh = fpfh / np.linalg.norm(fpfh)
其中get_spfh函数就是求解每一个特征点的 [ α , ϕ , θ ] [\alpha,\phi,\theta] [α,ϕ,θ]三元组,具体查看代码
2.FPFH完整代码即仿真效果
代码参见:大佬的代码,由于原作者的源代码中并没有添加坐标系的显示,不方便直观地的进行box的提取,故自己添加进去。并且自己也加了一些注释,希望对大家有所帮助。
数据集:chair_0001.txt 密码 :7875
main.py----主函数
import argparse
# IO utils:
from utils.io import read_modelnet40_normal
# detector:
from detection.iss import detect
# descriptor:
from description.fpfh import describe
import numpy as np
import pandas as pd
import open3d as o3d
import seaborn as sns
import matplotlib.pyplot as plt
if __name__ == '__main__':
# parse arguments:
input = "E:\资料\三维重建课程\\3D-Point-Cloud-Analytics-master\\3D-Point-Cloud-Analytics-master\workspace\data\modelnet40_normal_resampled\modelnet40_normal_resampled\chair\chair_0001.txt"
radius = 0.05
# 加载点云
point_cloud = read_modelnet40_normal(input)
# 建立搜索树
search_tree = o3d.geometry.KDTreeFlann(point_cloud)
# detect keypoints:
keypoints = detect(point_cloud, search_tree, radius)
# 可视化
point_cloud.paint_uniform_color([0.50, 0.50, 0.50])
# show roi:
max_bound = point_cloud.get_max_bound()
min_bound = point_cloud.get_min_bound()
center = (min_bound + max_bound) / 2.0
print("min_bound:",min_bound[0],min_bound[1],min_bound[2])
print("max_bound:", max_bound[0], max_bound[1], max_bound[2])
print("center:",center[0],center[1],center[2])
#椅子的平面[-0.1,0.1],椅子角为[-0.8,-0.6]
min_bound[1]=-0.1
max_bound[1]=0.1
# min_bound[1] = max_bound[1] - 0.1
# max_bound[1] = max_bound[1]
# min_bound[2] = center[2]
# max_bound[2] = max_bound[2]
#可视化提取ROI区域内的特征点
bounding_box = o3d.geometry.AxisAlignedBoundingBox(min_bound=min_bound,max_bound=max_bound)
roi = point_cloud.crop(bounding_box)
roi.paint_uniform_color([1.00, 0.00, 0.00])
keypoints_in_roi = keypoints.loc[
(
((keypoints['x'] >= min_bound[0]) & (keypoints['x'] <= max_bound[0])) &
((keypoints['y'] >= min_bound[1]) & (keypoints['y'] <= max_bound[1])) &
((keypoints['z'] >= min_bound[2]) & (keypoints['z'] <= max_bound[2]))
),:]
print("筛选后的特征点的个数:",len(keypoints_in_roi['id']))
np.asarray(point_cloud.colors)[ keypoints_in_roi['id'].values, :] = [1.0, 0.0, 0.0]
# 添加坐标系
FOR1 = o3d.geometry.TriangleMesh.create_coordinate_frame(size=1, origin=[0, 0, 0])
o3d.visualization.draw_geometries([FOR1,point_cloud])
# 计算特征点的描述子:
df_signature_visualization = []
for keypoint_id in keypoints_in_roi['id'].values:
signature = describe(point_cloud, search_tree, keypoint_id, radius,20) #B=20
df_ = pd.DataFrame.from_dict({'index': np.arange(len(signature)),'feature': signature})
df_['keypoint_id'] = keypoint_id
df_signature_visualization.append(df_)
df_signature_visualization = pd.concat(df_signature_visualization)
#保存特征点的描述子,以data,csv的格式进行保存,可用EXCEL打开查看
df_signature_visualization.to_csv("data.csv",encoding='utf-8')
#在求椅子的平面时,df_signature_visualization为215*3B,其中215为特征点的个数,故head里面不要超过3B
df_signature_visualization = df_signature_visualization.head(60)
# 画线
plt.figure(num=None, figsize=(16, 9))
sns.lineplot(
x="index", y="feature",
hue="keypoint_id", style="keypoint_id",
markers=True, dashes=False, data=df_signature_visualization
)
plt.title('Description Visualization for Keypoints')
plt.show()
fpfh.py----特征描述子
import numpy as np
import pandas as pd
import open3d as o3d
## 入口函数
# 输入:point_cloud: 点云数据
# search_tree: 点云搜索树
# keypoint_id: 关键点的索引
# radius: r领域半径
# B: 每个描述子特殊的维度,fpfh中为[α,ф,θ],最终描述子的维度为3B
# 输出:3B描述子
def get_spfh(point_cloud, search_tree, keypoint_id, radius, B):
# points handler:
points = np.asarray(point_cloud.points)
# get keypoint:
keypoint = np.asarray(point_cloud.points)[keypoint_id]
# find radius nearest neighbors:
[k, idx_neighbors, _] = search_tree.search_radius_vector_3d(keypoint, radius)
# remove query point:
idx_neighbors = idx_neighbors[1:]
# get normalized diff:
diff = points[idx_neighbors] - keypoint
diff /= np.linalg.norm(diff, ord=2, axis=1)[:,None] #diff 维数(k*3)
# get n1:
n1 = np.asarray(point_cloud.normals)[keypoint_id]
# get u:
u = n1 # u维数(3,)
# get v:
v = np.cross(u, diff) # v维数(k*3)
# get w:
w = np.cross(u, v) # 维数(k*3)
# get n2:
n2 = np.asarray(point_cloud.normals)[idx_neighbors] #n2维数(k*3)
# get alpha:
alpha = (v * n2).sum(axis=1) #alpha维数(k,)
alpha_min,alpha_max=min(alpha),max(alpha)
# get phi:
phi = (u*diff).sum(axis=1) #phi维数(k,)
phi_min, phi_max = min(phi), max(phi)
# get theta:
theta = np.arctan2((w*n2).sum(axis=1), (u*n2).sum(axis=1)) #theta维数(k,)
theta_min, theta_max = min(theta), max(theta)
# 因为histogram返回值有两个参数,[0]选择第一个参数
alpha_histogram = np.histogram(alpha, bins=B, range=(-1.0, +1.0))[0]
alpha_histogram = alpha_histogram / alpha_histogram.sum()
# get phi histogram:
phi_histogram = np.histogram(phi, bins=B, range=(-1.0, +1.0))[0]
phi_histogram = phi_histogram / phi_histogram.sum()
# get theta histogram:
theta_histogram = np.histogram(theta, bins=B, range=(-np.pi, +np.pi))[0]
theta_histogram = theta_histogram / theta_histogram.sum()
# build signature:
#hstack进行水平扩展,vstack进行竖直扩展
signature = np.hstack((alpha_histogram,phi_histogram,theta_histogram)) #维数(3*B,)
return signature
## 入口函数
# 输入:point_cloud: 点云数据
# search_tree: 点云搜索树
# keypoint_id: 关键点的索引
# radius: r领域半径
# B: 每个描述子特殊的维度,fpfh中为[α,ф,θ],最终描述子的维度为3B
# 输出:fpfh的结果
def describe(point_cloud, search_tree, keypoint_id, radius, B):
# points handler:
points = np.asarray(point_cloud.points)
# get keypoint:
keypoint = np.asarray(point_cloud.points)[keypoint_id]
# find radius nearest neighbors:
[k, idx_neighbors, _] = search_tree.search_radius_vector_3d(keypoint, radius)
if k <= 1:
return None
# remove query point:
idx_neighbors = idx_neighbors[1:]
# weights:
w = 1.0 / np.linalg.norm(points[idx_neighbors] - keypoint, ord=2, axis=1)
# SPFH from neighbors:
X = np.asarray([get_spfh(point_cloud, search_tree, i, radius, B) for i in idx_neighbors])
# neighborhood contribution:
spfh_neighborhood = 1.0 / (k - 1) * np.dot(w, X)
# query point spfh:
spfh_query = get_spfh(point_cloud, search_tree, keypoint_id, radius, B)
# finally:
fpfh = spfh_query + spfh_neighborhood
# normalize again:
fpfh = fpfh / np.linalg.norm(fpfh)
return fpfh
iss.py—特征点的提取
import heapq
import numpy as np
import pandas as pd
import open3d as o3d
def detect(point_cloud, search_tree, radius):
# points handler:
points = np.asarray(point_cloud.points)
# keypoints container:
keypoints = {'id': [],'x': [],'y': [],'z': [],'lambda_0': [],'lambda_1': [],'lambda_2': []}
# cache for number of radius nearest neighbors:
num_rnn_cache = {}
# heapq for non-maximum suppression:
pq = []
for idx_center, center in enumerate(points):
# find radius nearest neighbors:
[k, idx_neighbors, _] = search_tree.search_radius_vector_3d(center, radius)
# for each point get its nearest neighbors count:
w = []
deviation = []
for idx_neighbor in np.asarray(idx_neighbors[1:]):
# check cache:
if not idx_neighbor in num_rnn_cache:
[k_, _, _] = search_tree.search_radius_vector_3d(points[idx_neighbor], radius)
num_rnn_cache[idx_neighbor] = k_
# update:
w.append(num_rnn_cache[idx_neighbor])
deviation.append(points[idx_neighbor] - center)
# calculate covariance matrix:
w = np.asarray(w)
deviation = np.asarray(deviation)
cov = (1.0 / w.sum()) * np.dot(deviation.T,np.dot(np.diag(w), deviation))
# get eigenvalues:
w, _ = np.linalg.eig(cov)
w = w[w.argsort()[::-1]]
# add to pq:
heapq.heappush(pq, (-w[2], idx_center))
# add to dataframe:
keypoints['id'].append(idx_center)
keypoints['x'].append(center[0])
keypoints['y'].append(center[1])
keypoints['z'].append(center[2])
keypoints['lambda_0'].append(w[0])
keypoints['lambda_1'].append(w[1])
keypoints['lambda_2'].append(w[2])
# non-maximum suppression:
suppressed = set()
while pq:
_, idx_center = heapq.heappop(pq)
if not idx_center in suppressed:
# suppress its neighbors:
[_, idx_neighbors, _] = search_tree.search_radius_vector_3d(points[idx_center], radius)
for idx_neighbor in np.asarray(idx_neighbors[1:]):
suppressed.add(idx_neighbor)
else:
continue
# format:
keypoints = pd.DataFrame.from_dict(keypoints)
# first apply non-maximum suppression:
keypoints = keypoints.loc[keypoints['id'].apply(lambda id: not id in suppressed),keypoints.columns]
# then apply decreasing ratio test:
keypoints = keypoints.loc[(keypoints['lambda_0'] > keypoints['lambda_1']) &(keypoints['lambda_1'] > keypoints['lambda_2']),keypoints.columns]
return keypoints
io.py—读取modelbet40_normal
import pandas as pd
import open3d as o3d
def read_modelnet40_normal(filepath):
# load data:
df_point_cloud_with_normal = pd.read_csv(
filepath, header=None
)
# add colunm names:
df_point_cloud_with_normal.columns = [
'x', 'y', 'z',
'nx', 'ny', 'nz'
]
point_cloud = o3d.geometry.PointCloud()
point_cloud.points = o3d.utility.Vector3dVector(
df_point_cloud_with_normal[['x', 'y', 'z']].values
)
point_cloud.normals = o3d.utility.Vector3dVector(
df_point_cloud_with_normal[['nx', 'ny', 'nz']].values
)
return point_cloud
仿真效果
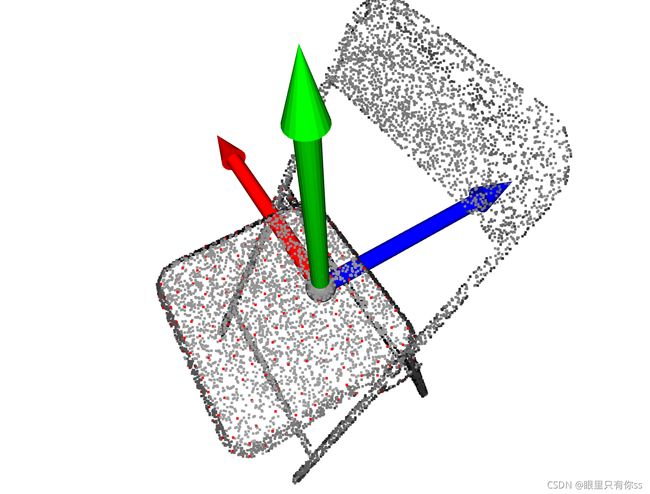
1.椅子平面,特征点图
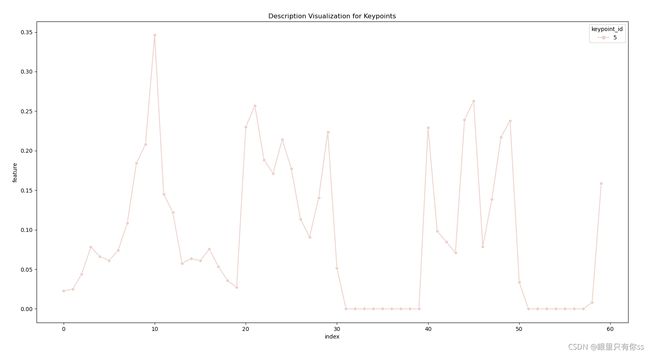
1.椅子平面,直方图
说明:在仿真的时候,我并没有仿真出原作者代码的效果,由于自己不会panads,会的小伙伴可以参考修改。其中图列是keypoint_id 3,其中这个3表示第一个特征点的序号,一个特征点包含3B个特征描述,本图只是显示第一个特征点,对该部分可以查看程序保存的data.csv,一切的迷惑就解开了。

2.椅子角,特征点图

2.椅子角,直方图