MATLAB函数极限和微分运算
| 函数名 | 功能 | 数学表达式 | MATLAB命令 |
|---|---|---|---|
| 幂函数 | 求x的a次幂 | x a x^a xa | x^a |
| 求x的平方根 | x \sqrt x x | sqrt(x) | |
| 指数函数 | 求a的x次幂 | a x a^x ax | a^x |
| 求e的x次幂 | e x e ^x ex | exp(x) | |
| 对数函数 | 求x的自然对数 | ln | log(x) |
| 求x的以2为底的对数 | l o g 2 x log_2x log2x | log2(x) | |
| 求x的以10为底的对数 | l o g 10 x log_{10}x log10x | log10(x) | |
| 三角函数 | 正弦函数 | sin | sin(x) |
| 余弦函数 | cos | cos(x) | |
| 正切函数 | tan | tan(x) | |
| 余切函数 | cot | cot(x) | |
| 正割函数 | sec | sec(x) | |
| 余割函数 | csc | csc(x) | |
| 反三角函数 | 反正弦函数 | arcsin | asin(x) |
| 反余弦函数 | arccos | acos(x) | |
| 反正切函数 | arctan | atan(x) | |
| 反余切函数 | arccot | acot(x) | |
| 反正割函数 | arcsec | asec(x) | |
| 反余割函数 | arccsc | acsc(x) | |
| 绝对值函数 | 求x的绝对值 | ∣ x ∣ \vert x \vert ∣x∣ | abs(x) |
定义函数() = x 3 + s i n x + x l o g x + e a r c t a n x + 1 \sqrt{x^3 + sinx} + xlogx + e^{arctanx+1} x3+sinx+xlogx+earctanx+1,并求(1.34)
function y=f(x)
y=sqrt(x^3+sin(x))+x*log(x)+exp(atan(x)+1);

求极限 S = lim x → + ∞ ( 1 + a x ) x S=\lim\limits_{x \rightarrow +\infty} (1+\frac{a}{x})^x S=x→+∞lim(1+xa)x。
clear
syms x a
F=(1+a/x)^x
limit(F, x, inf, 'left')

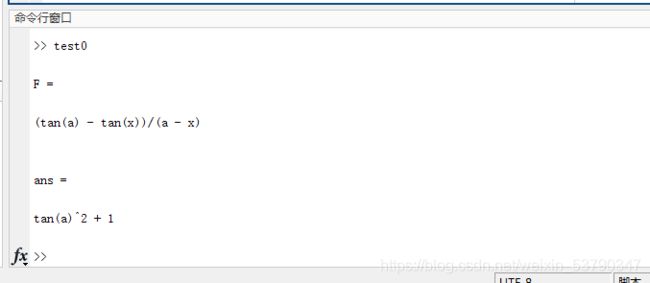
求极限 lim x → a t a n x − t a n a x − a ( 0 < a < π 2 ) \lim\limits_{x \rightarrow a} \frac{tanx-tana}{x-a}(0
clear
syms x a
F=(tan(x)-tan(a))/(x-a)
limit(F,x,a)
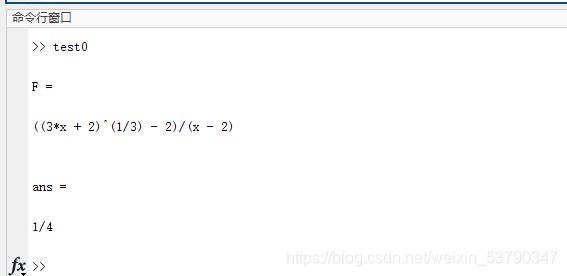
求极限 lim x → 2 3 x + 2 3 − 2 x − 2 \lim\limits_{x \rightarrow 2} \frac{\sqrt[3]{3x+2}-2}{x-2} x→2limx−233x+2−2
clear
syms x
F=((3*x+2)^(1/3)-2)/(x-2)
limit(F,x,2)
求极限 lim x → ∞ n ( 1 − 2 n − 1 2 n ) \lim\limits_{x \rightarrow \infty}n( 1-\frac{\sqrt{2n-1}}{2n}) x→∞limn(1−2n2n−1)
clear
syms n
F=n*(1-sqrt((2*n-1)/(2*n)))
limit(F,n,inf)

求函数 y = l n x + 2 1 − x y= ln \frac{x+2}{1−x} y=ln1−xx+2的一阶和三阶导数
clear;
syms x
y=log((x+2)/(1-x));
dy=diff(y,x)
dy3=diff(y,x,3)
pretty(dy3)

设 y = l n ( 1 x 2 + e 1 x ) + a r c t a n ( 1 − x 2 ) , 求 d y d x y = ln(\frac{1}{x^2}+e^{\frac{1}{x}})+ arctan(1 − x^2) ,求\frac{dy}{dx} y=ln(x21+ex1)+arctan(1−x2),求dxdy
clear;
syms x
y=log(1/x/x+exp(1/x))+atan(1-x*x);
dy=diff(y,x)

设 y = a r c t a n ( x 3 + 2 ) + l o g x − 1 x + 1 , 求 d y d x y= arctan(x^3 + 2) + log\sqrt\frac{ {x−1}} {x+1} ,求\frac{dy}{dx} y=arctan(x3+2)+logx+1x−1,求dxdy
clear;
syms x
y=atan(x*x*x+2)+log(sqrt((x-1)/(x+1)));
dy=diff(y,x)

设 y = x 2 e − x + ( s i n x ) 2 x , 求 d 2 y d x 2 y= x^2e^{-x} + (sinx)^{2x},求\frac{d^2y}{dx^2} y=x2e−x+(sinx)2x,求dx2d2y
clear;
syms x
y=x*x*exp(-x)+(sin(x))^(2*x)
dy=diff(y,x,2)
