关于剑指offer2中62题关于约瑟夫环问题的记录
约瑟夫环问题
看了许多帖子,只有约瑟夫环这篇文章,讲的比较清楚,但还是想用简单的方式在此做个记录,方便自己下次回顾。
问题:
假设给定数组n,数组中的元素依次排序排成了一个圆,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
假设数组n,其元素如下所示:每次从这个数组里删除第3个数字,求最后剩下来的数字是几?
我们先给出最后剩下来的数字,答案为4,方便我们后续观察规律。

在第一轮中,我们可以看到需要剔除的第三个数字是3,同时最后剩下的数字4的下标是3。
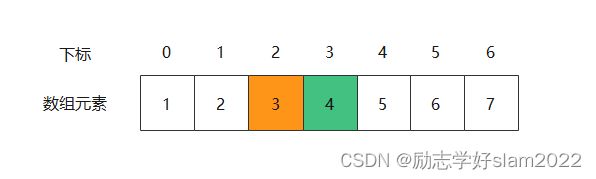
在第二轮中,我们可以看到需要剔除的第3个数字是6,同时最后剩下的数字4的下标是0。
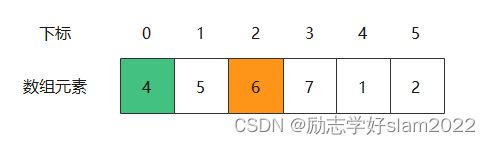
在第三轮中,我们可以看到需要剔除的第3个数字是2,同时最后剩下的数字4的下标是3。
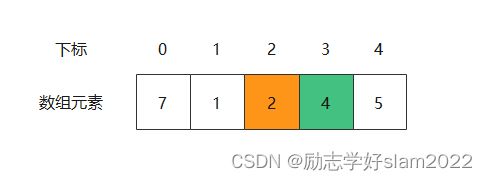
在第四轮中,我们可以看到需要剔除的第3个数字是7,同时最后剩下的数字4的下标是0。

在第五轮中,我们可以看到需要剔除的第3个数字是5,同时最后剩下的数字4的下标是1。
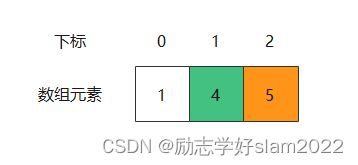
在第六轮中,我们可以看到需要剔除的第3个数字是1,同时最后剩下的数字4的下标是1。

第七轮就只剩下4一个数字了。4就是我们要求的数字了。
问题1:通过这种排列方式我们可以得到什么规律?
为方便观察,将总图附上:
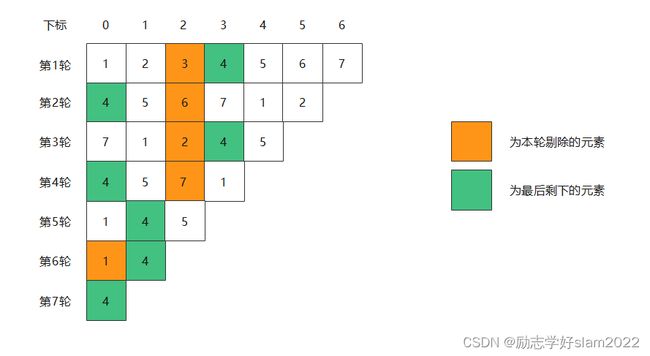
观察上图:我们可以发现,以这种排序的方式。无论数组中有多少个元素,最终我们得到的剩下来的数字 ,它的下标都为0。这一点很重要!
我们设 f ( f( f(N,m)表示,当数组元素的个数为N时,剔除第m位置的数字后,最终剩下来的数字的下标位置。
观察上图,可以发现每一轮中数字4的下标可以用该式表示为:
第1轮: f ( 7 , 3 ) = 3 f(7,3) = 3 f(7,3)=3
第2轮: f ( 6 , 3 ) = 0 f(6,3) = 0 f(6,3)=0
第3轮: f ( 5 , 3 ) = 3 f(5,3) = 3 f(5,3)=3
第4轮: f ( 4 , 3 ) = 0 f(4,3) = 0 f(4,3)=0
第5轮: f ( 3 , 3 ) = 1 f(3,3) = 1 f(3,3)=1
第6轮: f ( 2 , 3 ) = 1 f(2,3) = 1 f(2,3)=1
第7轮: f ( 1 , 3 ) = 0 f(1,3)= 0 f(1,3)=0
通过顺序递推,我们现在才真正得到了数组n中,最终剩下来的数字为4,且其下标为0,现在我们 进行逆向推导:
第1轮: f ( 1 , 3 ) = 0 f(1,3)= 0 f(1,3)=0
第2轮: f ( 2 , 3 ) = ( f ( 1 , 3 ) + 3 ) f(2,3) = (f(1,3) + 3) f(2,3)=(f(1,3)+3) % 2 = 1 2= 1 2=1
第3轮: f ( 3 , 3 ) = ( f ( 2 , 3 ) + 3 ) f(3,3) = (f(2,3) + 3) f(3,3)=(f(2,3)+3) % 3 = 1 3 = 1 3=1
第4轮: f ( 4 , 3 ) = ( f ( 3 , 3 ) + 3 ) f(4,3) = (f(3,3) + 3) f(4,3)=(f(3,3)+3) % 4 = 0 4 = 0 4=0
第5轮: f ( 5 , 3 ) = ( f ( 4 , 3 ) + 3 ) f(5,3) = (f(4,3) + 3) f(5,3)=(f(4,3)+3) % 5 = 3 5 = 3 5=3
第6轮: f ( 6 , 3 ) = ( f ( 5 , 3 ) + 3 ) f(6,3) = (f(5,3) + 3) f(6,3)=(f(5,3)+3) % 6 = 0 6 = 0 6=0
第7轮: f ( 7 , 3 ) = ( f ( 6 , 3 ) + 3 ) f(7,3) = (f(6,3) + 3) f(7,3)=(f(6,3)+3) % 7 = 3 7 = 3 7=3
这样我们就可以得到在数组n中,数字4的下标为3了。
以此继续递推:
当数组中元素为N时,我们删除第m个数字,最终剩下来的数字下标的求解方式可以写成通用公式:
i n d e x = f ( N , m ) = ( f ( N − 1 , m ) + m ) index = f(N,m) = (f(N-1,m) + m) index=f(N,m)=(f(N−1,m)+m) % N N N
问题2:为什么以这种方式进行排序?需要注意什么?
由题意,数组中的元素按照顺序排成了一个圆,也就是说这个数组中的元素是循环的,即数组中的末尾元素 的下一个元素是数组中的首元素。
注意点: 为什么通用公式中进行取模,也就是求余。因为数组的长度是有限的,不取模在代码实现中会导致内存溢出。以上题为例:
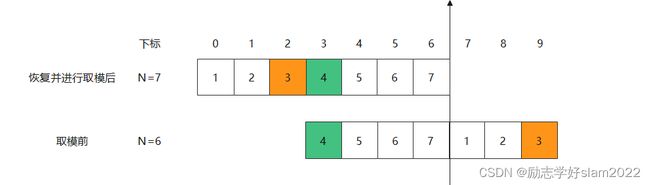
如上图,我们恢复逆向推导中的第六轮到第七轮的过程:
**step1:**逆向推导的第7轮,也就是顺序推导的第一轮,在顺一轮中,我们剔除了3,因此第一步就是恢复数字3,也就是在数组的末尾在右移3位。也就是+m
**step2:**进行取模,可以看到
取模前数字3的下标为9,对下标进形取模即 9 9 9% 7 = 2 7 = 2 7=2
取模前数字2的下标为8,对下标进形取模即 8 8 8% 7 = 1 7 = 1 7=1
取模前数字1的下标为7,对下标进形取模即 7 7 7% 7 = 0 7 = 0 7=0
刚好对应取模后的元素下标位置。
这样就实现了元素间的循环。
实现代码如下:
int lastRemaining(int n, int m){
int pos = 0;//对应前文中逆推的第一轮中最终剩下来的数字的位置:即f(1,3) = 0;
for(int i = 2; i <= n; i++)//从逆推中的第二轮开始遍历,即f(2,3),f(3,3),...
{
pos = (pos+ m) % i;//递推公式
}
return pos;
}