(DataWhale)图神经网络Task03:基于图神经网络GCN/GAT的节点表征与分类
文章目录
- Cora数据集的准备与分析
- TSNE可视化节点表征分布
- 图节点分类模型实现与对比(MLP vs. GCN vs. GAT)
-
- MLP分类模型
- GCN分类模型
- GAT分类模型
- 结果比较与分析
- 参考
Cora数据集的准备与分析
Cora是一个机器学习论文数据集,其中共有7个类别(num_classes:基于案例、遗传算法、 神经网络、概率方法、强化学习 、规则学习、理论。整个数据集中共有2708篇论文(num_nodes),在词干堵塞和去除词尾后,只剩下1433个独特的单词(num_node_features),文档频率小于10的所有单词都被删除。
from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures
dataset = Planetoid(root='dataset', name='Cora', transform=NormalizeFeatures())
print(f'Dataset: {dataset}:') #Dataset: Cora():
print(f'Number of graphs: {len(dataset)}') #Number of graphs: 1
print(f'Number of features: {dataset.num_features}') #Number of features: 1433
print(f'Number of classes: {dataset.num_classes}') #Number of classes: 7
data = dataset[0]
print(data) #Data(edge_index=[2, 10556], test_mask=[2708], train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
print(f'Number of nodes: {data.num_nodes}') #Number of nodes: 2708
print(f'Number of edges: {data.num_edges}') #Number of edges: 10556
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') #Average node degree: 3.90
print(f'Number of training nodes: {data.train_mask.sum()}') #Number of training nodes: 140
print(f'Contains self-loops: {data.contains_self_loops()}') #Contains self-loops: False
print(f'Is undirected: {data.is_undirected()}') #Is undirected: True
transform在将数据输入到神经网络之前修改数据,这一功能可用于实现数据规范化或数据增强;NormalizeFeatures对节点特征归一化,使各节点特征总和为1;
- 常见其余类型
transform:Compose封装一系列的transforms;ToSparseTensor将edge_index转化为torch_sparse.SparseTensor类型;ToUndirected将图转化为无向图;Constant为每个节点特征增加一个常量;RandomTranslate在一定范围内随机平移每个点,增加坐标上的扰动,可做数据增强;类似的还有RandomScale、RandomRotate、RandomShear;AddSelfLoops为每条边增加self-loop;RemoveIsolatedNodes移除图中孤立节点;KNNGraph根据节点位置pos生成KNN最近邻图,k值自定义,如pre_transform=T.KNNGraph(k=6);TwoHop添加节点间的两跳连接关系到边索引;- ···
TSNE可视化节点表征分布
- t-SNE 算法,全称为
t-distributed Stochastic Neighbor Embedding,即t分布-随机邻近嵌入。其本质是一种嵌入模型,能够将高维空间中的数据映射到低维空间中,并保留数据集的局部特性,是目前效果很好的数据降维和可视化方法之一; - 原理描述,t-SNE将数据点之间的相似度转化为条件概率,原始空间中数据点的相似度由
高斯联合分布表示,嵌入空间中数据点的相似度由学生t分布表示;通过原始空间和嵌入空间的联合概率分布的KL散度来评估嵌入效果的好坏,即将KL散度的函数作为损失函数,通过梯度下降算法最小化损失函数,最终获得收敛结果。
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
def visualize(h, color):
z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
plt.figure(figsize=(10,10))
plt.xticks([])
plt.yticks([])
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()
sklearn.manifold.TSNE(n_components=2, perplexity=30.0, ...),其中,n_components指定想要降维的维度,perplexity表示如何在局部或者全局位面上平衡关注点,也就是对每个点周围邻居数量猜测。fit_transform(X[, y])方法将X嵌入低维空间并返回转换后的输出;此外,TSNE还有get_params([deep])和set_params(**params)方法获取或自行设置降维模型参数。
图节点分类模型实现与对比(MLP vs. GCN vs. GAT)
MLP分类模型
import torch
from torch.nn import Linear
import torch.nn.functional as F
# MLP网络定义
class MLP(torch.nn.Module):
def __init__(self, hidden_channels):
super(MLP, self).__init__()
torch.manual_seed(12345)
self.lin1 = Linear(dataset.num_features, hidden_channels)
self.lin2 = Linear(hidden_channels, dataset.num_classes)
def forward(self, x):
x = self.lin1(x)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.lin2(x)
return x
# MLP网络训练函数
def train():
model.train()
optimizer.zero_grad()
out = model(data.x) #输入初始节点表征:torch.Size([2708, 1433])
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
# MLP网络测试函数
def test():
model.eval()
out = model(data.x)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc, out
model = MLP(hidden_channels=16)
#MLP(
# (lin1): Linear(in_features=1433, out_features=16, bias=True)
# (lin2): Linear(in_features=16, out_features=7, bias=True)
#)
# 训练
criterion = torch.nn.CrossEntropyLoss() # CrossEntropyLoss结合有LogSoftmax和NLLLoss两个类
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
for epoch in range(1, 201):
loss = train()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
# 测试与可视化
test_acc, out = test()
print(f'Test Accuracy: {test_acc:.4f}')
visualize(out, color=data.y) # MLP分类结果可视化
visualize(data.x, color=data.y) # 原始数据的可视化
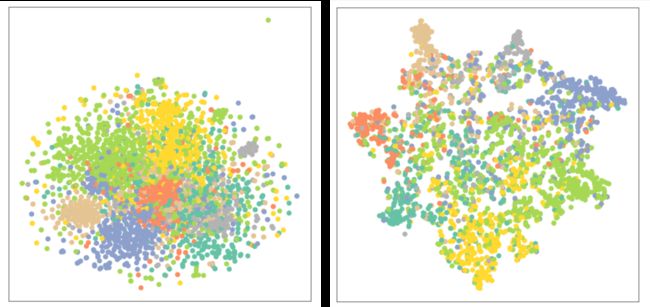
- MLP表征分布(右)与原数据分布(左)的对比见下图:
GCN分类模型
-
经典图卷积网络来自对切比雪夫网络(1)的简化,即将切比雪夫网络中的多项式卷积核限定为1阶,这样导致节点只能被它周围的1阶节点影响,为此叠加K层这样的图卷积,就可以将节点的影响力扩展到K阶邻居节点。
y = U ∑ k = 0 K θ T k ( Λ ~ ) U T x = ∑ k = 0 K θ k T k ( L ~ ) x c a u s e d : y = g θ ( L ) x = g θ ( U Λ U T ) x = U g θ ( Λ ) U T x (1) y = U \sum_{k=0}^{K} \theta T_{k}(\tilde{\Lambda}) U^{T} x=\sum_{k=0}^{K} \theta_{k} T_{k}(\tilde{L}) x \tag{1} \\ caused:y=g_{\theta}(L)x=g_{\theta}(U \Lambda U^T)x=Ug_{\theta}(\Lambda)U^Tx y=Uk=0∑KθTk(Λ~)UTx=k=0∑KθkTk(L~)xcaused:y=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx(1)
其中, L ~ = 2 L / λ m a x − I n \tilde{L}=2L/{\lambda_{max}}-I_{n} L~=2L/λmax−In;将谱域图卷积中的卷积核 g θ g_\theta gθ看作拉普拉斯矩阵 L L L特征值 Λ \Lambda Λ的函数 g θ ( Λ ) g_\theta (\Lambda) gθ(Λ)。进一步,将 T k ( L ~ ) T_{k}(\tilde{L}) Tk(L~)限定为1阶,且拉普拉斯矩阵的最大特征值可近似去 λ m a x ≈ 2 \lambda_{max} \approx 2 λmax≈2,那么 y ≈ θ 0 T 0 ( L ~ ) x θ 1 T 1 ( L ~ ) x = θ 0 x + θ 1 D − 1 / 2 A D − 1 / 2 x y \approx {\theta}_0 T_0(\tilde L)x {\theta}_1 T_1(\tilde L)x = {\theta}_0 x + {\theta}_1 D^{-1/2} A D^{-1/2} x y≈θ0T0(L~)xθ1T1(L~)x=θ0x+θ1D−1/2AD−1/2x,最终有:
Y = D ~ − 1 / 2 A ~ D ~ − 1 / 2 X Θ {Y}= {\tilde{D}}^{-1/2} {\tilde{A}}{\tilde{D}}^{-1/2}{X}{\Theta} Y=D~−1/2A~D~−1/2XΘ其中, A ~ = A + I {\tilde{A}} = {A} + {I} A~=A+I表示插入自环的邻接矩阵, D ~ i i = ∑ j = 0 A ~ i j \tilde{D}_{ii} = \sum_{j=0} \tilde{A}_{ij} D~ii=∑j=0A~ij表示 A ^ {\hat{A}} A^的对角线度矩阵。
-
在实际应用中,通过叠加多层图卷积,可得到一个图卷积网络。以 H l H^l Hl表示第 l l l层的节点向量, W l W^l Wl表示对应层的参数,定义 A ^ = D ~ − 1 / 2 A ~ D ~ − 1 / 2 \hat{A}={\tilde{D}}^{-1/2}{\tilde{A}}{\tilde{D}}^{-1/2} A^=D~−1/2A~D~−1/2,那么每层图卷积可以正式定义为:
H l + 1 = f ( H l , A ) = σ ( A ^ H l W l ) H^{l+1} = f(H^l, {A}) = \sigma ({\hat{A}H^l W^l}) Hl+1=f(Hl,A)=σ(A^HlWl) -
PyG中
GCNConv模块:GCNConv(in_channels: int, out_channels: int, improved: bool = False, cached: bool = False, add_self_loops: bool = True, normalize: bool = True, bias: bool = True, **kwargs):in_channels:输入数据维度;out_channels:输出数据维度;improved:如果为true, A ^ = A + 2 I \mathbf{\hat{A}} = \mathbf{A} + 2\mathbf{I} A^=A+2I,其目的在于增强中心节点自身信息;cached:是否存储 D ^ − 1 / 2 A ^ D ^ − 1 / 2 \mathbf{\hat{D}}^{-1/2} \mathbf{\hat{A}} \mathbf{\hat{D}}^{-1/2} D^−1/2A^D^−1/2的计算结果以便后续使用,这个参数只应在归纳学习(transductive learning)的场景中设置为true;add_self_loops:是否在邻接矩阵中增加自环边;normalize:是否添加自环边并在运行中计算对称归一化系数;bias:是否包含偏置项。
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
# GCN网络定义
class GCN(torch.nn.Module):
def __init__(self, hidden_channels):
super(GCN, self).__init__()
torch.manual_seed(12345)
self.conv1 = GCNConv(dataset.num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
# GCN网络训练函数
def train():
model.train()
optimizer.zero_grad()
out = model(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
# GCN网络测试函数
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc, out
model = GCN(hidden_channels=16)
#GCN(
# (conv1): GCNConv(1433, 16)
# (conv2): GCNConv(16, 7)
#)
# GCN未经训练时的输出——节点表征,及可视化
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
# 训练
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
for epoch in range(1, 201):
loss = train()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
# 测试与可视化
test_acc, out = test()
print(f'Test Accuracy: {test_acc:.4f}')
visualize(out, color=data.y)
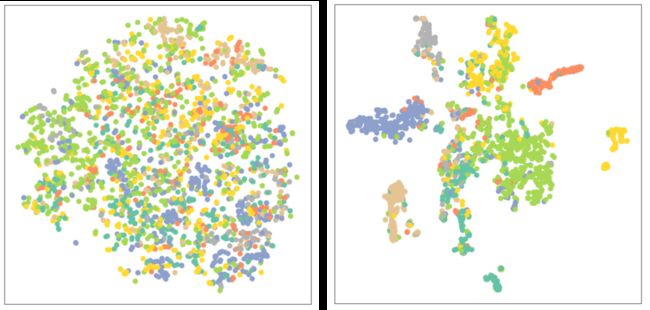
- 未经训练的GCN表征分布(左)与训练后的GCN表征分布(右)图:
GAT分类模型
-
基本思想:在图结构中,节点与节点之间的重要性是不同的,在图神经网络中应用注意力机制为各节点赋予不同权重,从而抽取更关键的信息,达到更好效果。
-
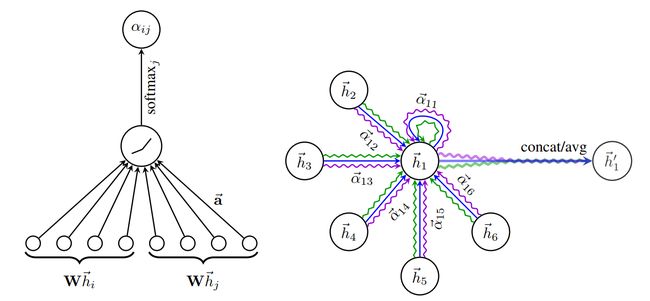
GAT结构示意图:
- 通过一个共享的注意力机制 a t t att att计算节点间的自注意力: e i j = a t t ( W h i , W h j ) e_{ij}=att(Wh_{i}, Wh_{j}) eij=att(Whi,Whj);其中, W W W是一个共享权重,权重 e i j e_{ij} eij表示节点 j j j相对节点 i i i的重要度;GAT一般选择一个单层前馈网络和非线性激活函数 L e a k y R e L U LeakyReLU LeakyReLU来计算 e i j = L e a k y R e L U ( a [ W h i ∥ W h j ] ) e_{ij}=\mathrm{LeakyReLU}(a[Wh_i \Vert Wh_j]) eij=LeakyReLU(a[Whi∥Whj]);
- 临接节点注意力的归一化: α i , j = S o f t m a x j ( e i j ) = exp ( L e a k y R e L U ( a [ W h i ∥ W x j ] ) ) ∑ k ∈ N i ∪ ( i ) exp ( L e a k y R e L U ( a [ W h i ∥ W h k ] ) ) \alpha_{i,j} = Softmax_j(e_{ij})=\frac{\exp ({LeakyReLU}({a}[W{h}_i \Vert W{x}_j]))}{\sum_{k \in \mathcal{N}_{i} \cup(i)}\exp({LeakyReLU}({a}[W{h}_i \Vert W{h}_k]))} αi,j=Softmaxj(eij)=∑k∈Ni∪(i)exp(LeakyReLU(a[Whi∥Whk]))exp(LeakyReLU(a[Whi∥Wxj]));
- 根据注意力权重融合临接节点信息,更新后的节点特征为: h i ′ = σ ( α i , i W h i + ∑ j ∈ N i α i , j W h j ) h^{\prime}_i=\sigma(\alpha_{i,i}W{h}_{i} + \sum_{j \in \mathcal{N}_{i}} \alpha_{i,j}W{h}_{j}) hi′=σ(αi,iWhi+∑j∈Niαi,jWhj);
- K头注意力,见上图右侧,非最后一层多头注意力的拼接: h i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i ∪ ( i ) α i j k W k h j ) {h}_{i}^{\prime}=\|_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i} \cup (i)} \alpha_{i j}^{k} {W}^{k} {h}_{j}\right) hi′=∥k=1Kσ(∑j∈Ni∪(i)αijkWkhj);最后一层多头注意力的平均: h i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i ∪ ( i ) α i j k W k h j ) {h}_{i}^{\prime}=\sigma(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i} \cup (i)} \alpha_{i j}^{k} {W}^{k}{h}_{j}) hi′=σ(K1∑k=1K∑j∈Ni∪(i)αijkWkhj)。
-
PyG中
GATConv模块:GATConv(in_channels: Union[int, Tuple[int, int]], out_channels: int, heads: int = 1, concat: bool = True, negative_slope: float = 0.2, dropout: float = 0.0, add_self_loops: bool = True, bias: bool = True, **kwargs)。in_channels:输入数据维度;out_channels:输出数据维度;heads:在GATConv使用多少个注意力模型;concat:如为true,不同注意力模型得到的节点表征被拼接到一起(表征维度翻倍),否则对不同注意力模型得到的节点表征求均值;negative_slope:LeakyReLU负轴部分斜率,默认为0.2。
import torch
import torch.nn.functional as F
from torch_geometric.nn import GATConv
# GAT网络定义
class GAT(torch.nn.Module):
def __init__(self, hidden_channels):
super(GAT, self).__init__()
torch.manual_seed(12345)
self.conv1 = GATConv(dataset.num_features, hidden_channels)
self.conv2 = GATConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
# GAT网络训练函数
def train():
model.train()
optimizer.zero_grad()
out = model(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
# GAT网络测试函数
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc, out
model = GAT(hidden_channels=16)
#GAT(
# (conv1): GATConv(1433, 16, heads=1)
# (conv2): GATConv(16, 7, heads=1)
#)
# GAT未经训练时的输出——节点表征,及可视化
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
# 训练
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
for epoch in range(1, 201):
loss = train()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
# 测试与可视化
test_acc, out = test()
print(f'Test Accuracy: {test_acc:.4f}')
visualize(out, color=data.y)
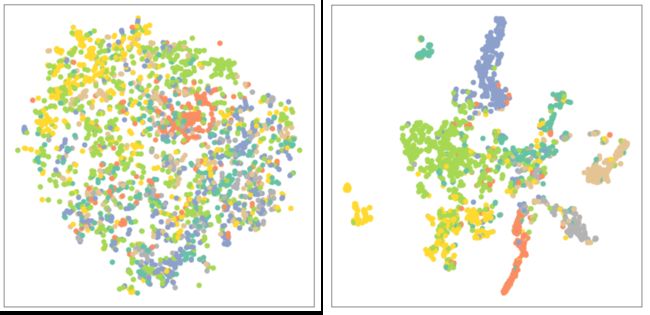
- 未经训练的GAT表征分布(左)与训练后的GAT表征分布(右)图:
结果比较与分析
- 在Cora节点表征分类任务上,GCN表现最好,GAT次之,MLP最差,表明边信息(消息传递机制)对于图节点嵌入影响很大;
- GAT所需训练轮次较少,易发生过拟合现象。
参考
- https://gitee.com/rongqinchen/team-learning-nlp/blob/master/GNN/Markdown%E7%89%88%E6%9C%AC/5-%E5%9F%BA%E4%BA%8E%E5%9B%BE%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E7%9A%84%E8%8A%82%E7%82%B9%E8%A1%A8%E5%BE%81%E5%AD%A6%E4%B9%A0.md
- https://pytorch-geometric.readthedocs.io/en/latest/modules/transforms.html#torch-geometric-transforms
- 通俗理解一个常用的降维算法(t-SNE)
- 从图(Graph)到图卷积(Graph Convolution)
- 马腾飞《图神经网络:基础与前沿》