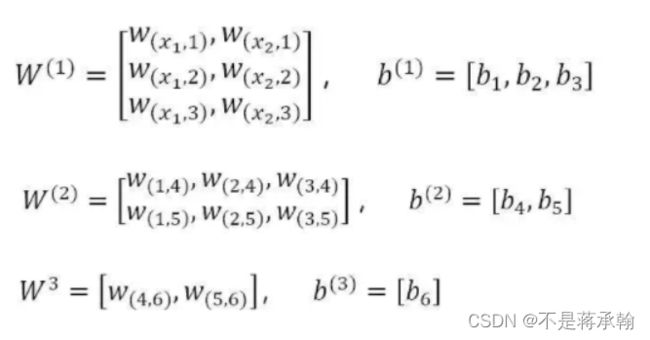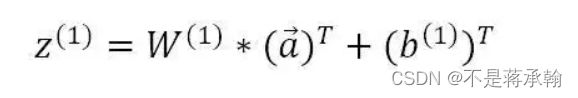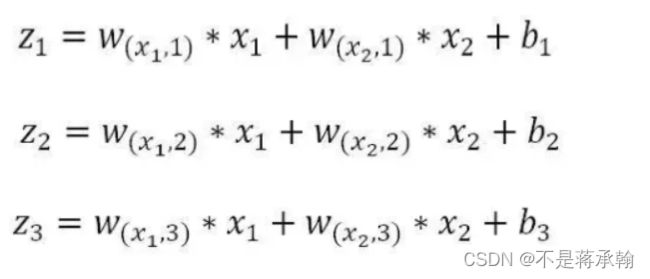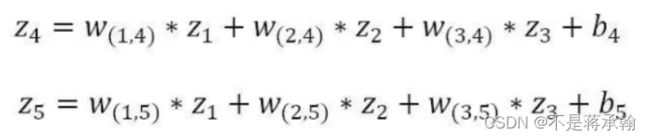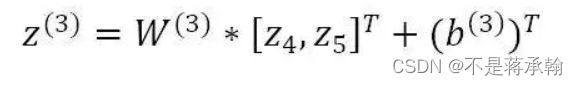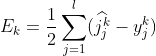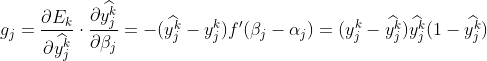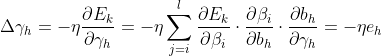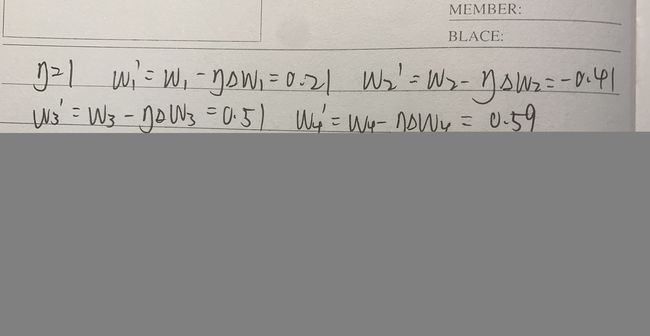HBU-NNDL 作业3：分别使用numpy和pytorch实现FNN例题
目录
一、过程推导 - 了解BP原理
1、前馈计算的过程
第二层隐藏层的计算：
输出层的计算
2、反向传播的计算
BP神经网络权值、阈值更新公式推导
二、数值计算 - 手动计算，掌握细节
三、代码实现 - numpy手推 + pytorch自动
1、对比【numpy】和【pytorch】程序，总结并陈述。
numpy版
pytorch版
2、激活函数Sigmoid用PyTorch自带函数torch.sigmoid()，观察、总结并陈述。
3、激活函数Sigmoid改变为Relu，观察、总结并陈述。
4、损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代，观察、总结并陈述。
5、损失函数MSE改变为交叉熵，观察、总结并陈述。
6、改变步长，训练次数，观察、总结并陈述。
7、权值w1-w8初始值换为随机数，对比“指定权值”的结果，观察、总结并陈述。
8、权值w1-w8初始值换为0，观察、总结并陈述。
9、全面总结反向传播原理和编码实现，认真写心得体会。
参考
一、过程推导 - 了解BP原理
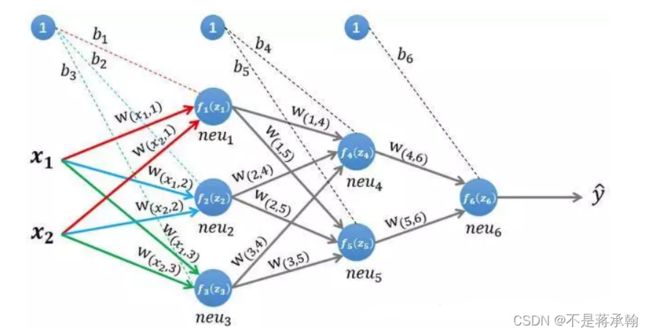
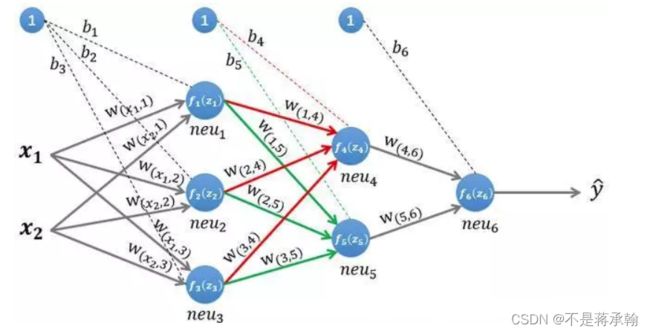
下面我们将以下图所示的神经网络，该图所示是一个三层神经网络，两层隐藏层和一层输出层，输入层有两个神经元，接收输入样本，为网络的输出。
1、前馈计算的过程
为了理解神经网络的运算过程，我们需要先搞清楚前馈计算，即数据沿着神经网络前向传播的计算过程，以上图所示的网络为例，输入的样本为：
三层网络的参数定义为：
第一层隐藏层的计算
第一层隐藏层有三个神经元：neu₁、neu₂和。neu₃该层的输入为：
以单个神经元为例，则其输入为：
假设我们选择函数f(x)作为该层的激活函数（图中的激活函数都标了一个下标，一般情况下，同一层的激活函数都是一样的，不同层可以选择不同的激活函数），那么该层的输出为：
、
和
。
第二层隐藏层的计算：
第二层隐藏层有两个神经元：neu₄和neu₅。该层的输入为：
即第二层的输入是第一层的输出乘以第二层的权重，再加上第二层的偏置。因此得到
和
的输入分别为：
该层的输出分别为：
和
。
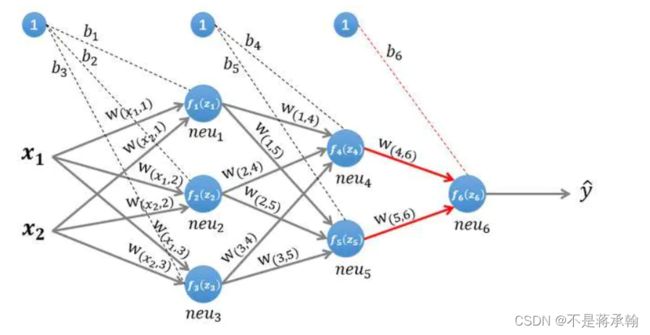
输出层的计算
输出层只有一个神经元：neu₆。该层的输入为：
即：
因为该网络要解决的是一个二分类问题，所以输出层的激活函数也可以使用一个Sigmoid型函数，神经网络最后的输出为
。
2、反向传播的计算
我们已经了解了数据沿着神经网络前向传播的过程，这一节我们来介绍更重要的反向传播的计算过程。假设我们使用随机梯度下降的方式来学习神经网络的参数，损失函数定义为，其中y是该样本的真实类标。使用梯度下降进行参数的学习，我们必须计算出损失函数关于神经网络中各层参数（权重w和偏置b）的偏导数。
假设我们要对第k层隐藏层的参数
和求偏导数
。假设
代表第k层神经元的输入，即
其中
为前一层神经元的输出，则根据链式法则有：
BP神经网络权值、阈值更新公式推导
此部分以西瓜书上的神经网络为例。
给定训练集:
即输入属性序列由
个属性描述，输出ll维实值向量。为了方便讨论，图1给出了拥有个输入神经元，
个输出神经元，
个隐层神经元的多层前馈网络结构，其中输出层为第
个神经元的阈值用
表示，隐层第
个神经元用
表示。输入层第
个神经元与隐层第个神经元之间的连接权为
,隐层第个神经元与输出层第个神经元之间的连接权为
。
记隐层第hh个神经元接收到的输入为
,输出层的第个神经元接收到的输入为: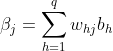
,其中
为隐层第个神经元的输出。现在假设隐层和输出层都使用Sigmoid函数：
对训练例
,假定神经网络的输出为：
,即：
(1)
则网络在(xk,yk)(xk,yk)上的均方误差为：
(2)
图1中的网络中有
个参数需要确定。BP是一个迭代学习算法，在迭代的每一轮采用广义的感知机学习规则对参数进行更新估计。下面我们以图中的隐层到输出层的连接权值为例来进行推导：
BP算法基于梯度下降(gradient descent)策略,以目标的负梯度方向对参数进行调整，对公式2中的误差
,给定学习率
,有：
(3)
注意到先影响到第个输出神经元的输入值
,再影响到其输出值
,然后影响到,有：
(4)
根据的定义有：
,并且Sigmoid函数有一个很好的性质：
，于是根据公式(1)和(2)，有：
(5)
将公式(5)带入到公式(4)，再带入到公式(3)中，就得到了BP算法中关于的更新公式：
(6)
而
的更新公式为：
(7)
BP神经网络的输出层到隐层的连接权值
的更新估计式为：
BP神经网络的隐层第个神经元的阈值
的更新公式为：
学习率
控制着算法每一轮迭代中的更新步长。
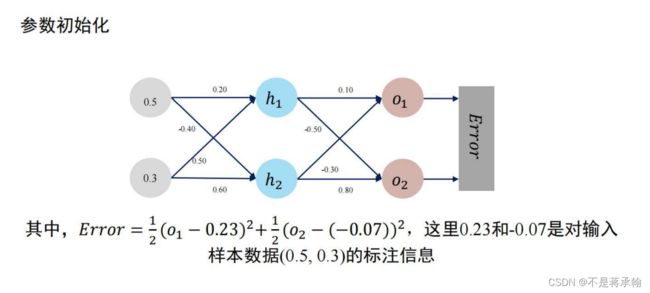
二、数值计算 - 手动计算，掌握细节
三、代码实现 - numpy手推 + pytorch自动
1、对比【numpy】和【pytorch】程序，总结并陈述。
numpy版
import numpy as np
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2)
print("正向计算：o1 ,o2")
print(round(out_o1, 5), round(out_o2, 5))
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
print("损失函数：均方误差")
print(round(error, 5))
return out_o1, out_o2, out_h1, out_h2
def back_propagate(out_o1, out_o2, out_h1, out_h2):
# 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
# print(round(d_o1, 2), round(d_o2, 2))
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
# print(round(d_w5, 2), round(d_w7, 2))
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
# print(round(d_w6, 2), round(d_w8, 2))
d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x2
# print(round(d_w1, 2), round(d_w3, 2))
d_w2 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x2
# print(round(d_w2, 2), round(d_w4, 2))
print("反向传播：误差传给每个权值")
print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
round(d_w7, 5), round(d_w8, 5))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 5
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
x1, x2 = 0.5, 0.3
y1, y2 = 0.23, -0.07
print("=====输入值：x1, x2；真实输出值：y1, y2=====")
print(x1, x2, y1, y2)
print("=====更新前的权值=====")
print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
for i in range(1000):
print("=====第" + str(i) + "轮=====")
out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))结果：
=====第10轮=====
正向计算：o1 ,o2
0.2987 0.16277
损失函数：均方误差
0.02945
反向传播：误差传给每个权值
0.0029 0.00252 0.00174 0.00151 0.00724 0.01596 0.00637 0.01405
=====第100轮=====
正向计算：o1 ,o2
0.23239 0.04193
损失函数：均方误差
0.00627
反向传播：误差传给每个权值
0.00027 0.00023 0.00016 0.00014 0.00019 0.00201 0.00017 0.00178
=====第999轮=====
正向计算：o1 ,o2
0.23038 0.00954
损失函数：均方误差
0.00316
反向传播：误差传给每个权值
4e-05 3e-05 2e-05 2e-05 3e-05 0.00029 2e-05 0.00026
更新后的权值
-0.84 -1.3 -0.13 0.06 -1.55 -7.31 -1.75 -5.23
pytorch版
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值：x1, x2；真实输出值：y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算：o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 ： t.nn.MSELoss()
print("损失函数（均方误差）：", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意：将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1000):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播，求 Loss，构建计算图
L.backward() # 自动求梯度，不需要人工编程实现。反向传播，求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)结果：
=====第10轮=====
正向计算：o1 ,o2
tensor([0.4047]) tensor([0.3507])
损失函数（均方误差）： 0.10375461727380753
grad W: -0.02 -0.0 -0.01 -0.0 0.02 0.06 0.02 0.05
=====第100轮=====
正向计算：o1 ,o2
tensor([0.2375]) tensor([0.0730])
损失函数（均方误差）： 0.010253453627228737
grad W: -0.0 -0.0 -0.0 -0.0 0.0 0.01 0.0 0.01
=====第999轮=====
正向计算：o1 ,o2
tensor([0.2296]) tensor([0.0098])
损失函数（均方误差）： 0.0031851977109909058
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.6515]) tensor([0.1770]) tensor([1.3709]) tensor([0.9462]) tensor([-0.7798]) tensor([-4.2741]) tensor([-1.0236]) tensor([-2.1999])
对比：
pytorch的反向传播不用自己手动计算传递误差，但是在参数更新完成后要将梯度清零。
2、激活函数Sigmoid用PyTorch自带函数torch.sigmoid()，观察、总结并陈述。
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = torch.sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = torch.sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = torch.sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = torch.sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算：o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2结果：
=====第999轮=====
正向计算：o1 ,o2
tensor([0.2296]) tensor([0.0098])
损失函数（均方误差）： 0.003185197012498975
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.6515]) tensor([0.1770]) tensor([1.3709]) tensor([0.9462]) tensor([-0.7798]) tensor([-4.2741]) tensor([-1.0236]) tensor([-2.1999])
结果和自己写的sigmoid函数效果相同
3、激活函数Sigmoid改变为Relu，观察、总结并陈述。
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = torch.relu(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = torch.relu(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = torch.relu(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = torch.relu(in_o2)
print("正向计算：o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2结果
=====第999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([0.])
损失函数（均方误差）： 0.0024500000290572643
grad W: -0.0 0.0 -0.0 0.0 -0.0 0.0 0.0 0.0
更新后的权值
tensor([0.4287]) tensor([-0.4000]) tensor([0.6372]) tensor([0.6000]) tensor([0.5672]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
第一，采用sigmoid等函数，算激活函数是（指数运算），计算量大；反向传播求误差梯度时，求导涉及除法，计算量相对大。而采用Relu激活函数，整个过程的计算量节省很多。
第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0），这种情况会造成信息丢失，梯度消失在网络层数多的时候尤其明显，从而无法完成深层网络的训练。
第三，ReLU会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。
4、损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代，观察、总结并陈述。
def loss_fuction(x1, x2, y1, y2):
y1_pred, y2_pred = forward_propagate(x1, x2)
t = torch.nn.MSELoss()
loss = t(y1_pred,y1) + t(y2_pred,y2)
print("损失函数（均方误差）：", loss.item())
return loss结果：
=====第999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([0.])
损失函数（均方误差）： 0.004900000058114529
grad W: -0.0 0.0 -0.0 0.0 -0.0 0.0 0.0 0.0
更新后的权值
tensor([0.4236]) tensor([-0.4000]) tensor([0.6342]) tensor([0.6000]) tensor([0.5720]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
总结：
手写的均方误差还是比torch.nn.MSELoss()训练效果好一点。
5、损失函数MSE改变为交叉熵，观察、总结并陈述。
def loss_fuction(x1, x2, y1, y2):
y1_pred, y2_pred = forward_propagate(x1, x2)
loss_func = torch.nn.CrossEntropyLoss() # 创建交叉熵损失函数
y_pred = torch.stack([y1_pred, y2_pred], dim=1)
y = torch.stack([y1, y2], dim=1)
loss = loss_func(y_pred, y) # 计算
print("损失函数（交叉熵损失）：", loss.item())
return loss
结果
=====第999轮=====
正向计算：o1 ,o2
tensor([0.9929]) tensor([0.0072])
损失函数（交叉熵损失）： -0.018253758549690247
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.2809]) tensor([0.6580]) tensor([1.7485]) tensor([1.2348]) tensor([3.8104]) tensor([-4.2013]) tensor([2.5933]) tensor([-2.0866])
交叉熵损失在训练1000轮后是个负数，当网络输出的概率是0-1时，正数。可当网络输出大于1的数，就有可能变成负数。
6、改变步长，训练次数，观察、总结并陈述。
步长为1
训练5000轮
=====第4999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([0.0010])
损失函数（均方误差）： 0.005036547780036926
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.2794]) tensor([0.6878]) tensor([1.7477]) tensor([1.2527]) tensor([-0.6800]) tensor([-5.6410]) tensor([-0.9468]) tensor([-3.2652])
训练10000轮
=====第9999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([0.0005])
损失函数（均方误差）： 0.004965716972947121
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.4531]) tensor([0.8572]) tensor([1.8519]) tensor([1.3543]) tensor([-0.6561]) tensor([-6.0367]) tensor([-0.9275]) tensor([-3.5846])
步长为0.1
训练5000轮
=====第4999轮=====
正向计算：o1 ,o2
tensor([0.2296]) tensor([0.0098])
损失函数（均方误差）： 0.006370754446834326
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.6543]) tensor([0.1820]) tensor([1.3726]) tensor([0.9492]) tensor([-0.7793]) tensor([-4.2709]) tensor([-1.0225]) tensor([-2.1971])
训练10000轮
=====第9999轮=====
正向计算：o1 ,o2
tensor([0.2298]) tensor([0.0050])
损失函数（均方误差）： 0.005628202576190233
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.8500]) tensor([0.3256]) tensor([1.4900]) tensor([1.0354]) tensor([-0.7459]) tensor([-4.6866]) tensor([-0.9968]) tensor([-2.5165])
步长为5
训练5000轮
=====第4999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([0.0002])
损失函数（均方误差）： 0.004924994893372059
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.6482]) tensor([1.0351]) tensor([1.9689]) tensor([1.4611]) tensor([-0.6280]) tensor([-6.5752]) tensor([-0.9151]) tensor([-4.0168])
训练10000轮
=====第9999轮=====
正向计算：o1 ,o2
tensor([0.2300]) tensor([8.6091e-05])
损失函数（均方误差）： 0.004912060219794512
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.8024]) tensor([1.2066]) tensor([2.0614]) tensor([1.5640]) tensor([-0.6095]) tensor([-6.9487]) tensor([-0.8996]) tensor([-4.3291])
步长在1和5时，训练效果差不多，在0.1时稍差。
7、权值w1-w8初始值换为随机数，对比“指定权值”的结果，观察、总结并陈述。
w1, w2, w3, w4, w5, w6, w7, w8 = torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1) #权重初始值
=====第999轮=====
正向计算：o1 ,o2
tensor([[0.2299]]) tensor([[0.0047]])
损失函数（均方误差）： 0.0055844783782958984
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([[1.3820]]) tensor([[1.1637]]) tensor([[1.9474]]) tensor([[0.7103]]) tensor([[-2.1091]]) tensor([[-4.3067]]) tensor([[0.6382]]) tensor([[-2.8800]])
随机赋值也依然能训练到很好的结果
8、权值w1-w8初始值换为0，观察、总结并陈述。
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor(
[0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]) # 权重初始值=====第999轮=====
正向计算：o1 ,o2
tensor([0.2298]) tensor([0.0048])
损失函数（均方误差）： 0.005598478484898806
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.3603]) tensor([1.3603]) tensor([0.8162]) tensor([0.8162]) tensor([-0.8444]) tensor([-3.7221]) tensor([-0.8444]) tensor([-3.7221])
最终结果还是一样，权重初始值只绘影响网络收敛速度，并不会影响或微小影响网络的收敛结果。
9、全面总结反向传播原理和编码实现，认真写心得体会。
1、numpy代码还是比较复杂，反向传播部分需要仔细一点，很容易把某个变量写错，而pytorch只需要一个backward()就可以搞定。
2、关于神经网络通过学习新增的理解是：
1）正则化，通过正则化可以解决noraml equation中的不满秩的问题即与其对应的过拟合问题。
2） 神经网络存在着欠拟合和过拟合的问题，解决问题一般是将所有数据分成三类，训练数据，交叉验证数据和测试数据，相应的会存在训练误差，交叉验证误差和测试误差三种。判断欠拟合和过拟合的方法是：如果训练误差很小，但是交叉验证误差很大，一般是过拟合；如训练误差和交叉验证的误差都比较大，且几乎相等，说明是欠拟合。
3）调整神经网络常用的几个方法：1) 获取更多的数据，修正过拟合。2）减少特征，修正过拟合（去除特征的相关性）。3）增加特征，修正欠拟合，4）加入多项式特征，修正欠拟合，5）加到正则化系数，修正过拟合，6）减小正则化系数，修正欠拟合。
3、关于超参数
1）BP神经网络我在学习的过程中模型参数主要觉得这几个需要关注（学习率，隐藏层神经元个数，隐藏层层数【默认为1】）
2）学习率一般范围是0.01-0.25，学习率太大容易过拟合，太小容易欠拟合，这里可以利用for循环，挨个试试，选取一个最好的参数。
3）隐藏层神经元有很多的经验公式确定，但是经验公式并不一定具有代表性，可以根据某个经验公式利用for进行尝试确定。
4）隐藏层层数这里就感觉要是模型输入参数复杂的话需要多设立一些，之前看的文献好像是十几个隐藏层，每层60个神经元，但是感觉有时候一层效果就整挺好。
参考
torch.sigmoid()、torch.nn.Sigmoid()和torch.nn.functional.sigmoid()三者之间的区别_沐风大大的博客-CSDN博客_torch.sigmoid
解释为什么BP神经网络中有的人使用二次代价函数，而有的人使用交叉熵_我曾记得曾经的博客-CSDN博客