ReLU,Sigmoid,Tanh,softmax【基础知识总结】

激活函数的引入是为了增加神经网络模型的非线性，没有激活函数每层就相当于矩阵相乘。每一层输出都是上层的输入的线性函数，无论神经网络多少层，输出都是输入的线性组合，就是最原始的感知机.
加入激活函数，给神经元引入非线性因素，神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

一、ReLU（Rectified Linear Activation Function）

ReLU全名Rectified Linear Unit，意思是修正线性单元。Relu激活函数是常用的神经激活函数。
ReLU函数其实是分段线性函数，把所有的负值都变为0，而正值不变，这种操作被成为单侧抑制。
如图:

1、优点

①ReLu具有稀疏性，可以使稀疏后的模型能够更好地挖掘相关特征，拟合训练数据；
②在x>0区域上，不会出现梯度饱和、梯度消失的问题；
③计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。

2、缺点

①输出不是0对称。
②由于小于0的时候激活函数值为0，梯度为0，所以存在一部分神经元永远不会得到更新。

补充

为了弥补sigmoid函数和tanh函数的缺陷所以出现了ReLU激活函数。

这些激活函数的出现有一个历史先后问题, sigmoid函数出现的早, ReLU是晚辈;其次，不存在绝对的说法让ReLU完胜其它任何方案,因为在很多时候,不试一试别的方案,谁都不敢拍胸脯说这个网络已经没法提升了, 这就是神经网络的特点。

ReLU激活函数求导不涉及浮点运算，所以速度更快。在z大于零时梯度始终为1；在z小于零时梯度始终为0；z等于零时的梯度可以当成1也可以当成0，实际应用中并不影响。
对于隐藏层，选择ReLU作为激活函数，能够保证z大于零时梯度始终为1，从而提高神经网络梯度下降算法运算速度。

二、Sigmoid

Sigmoid 激活函数 ， 也被称为 Logistic函数神经网络，传统上是一个非常受欢迎的神经网络激活函数。函数的输入被转换成介于0.0和1.0之间的值。大于1.0的输入被转换为值1.0，同样，小于0.0的值被折断为0.0。所有可能的输入函数的形状都是从0到0.5到1.0的 s 形。在很长一段时间里，直到20世纪90年代早期，这是神经网络的默认激活方式。
其作用就是引入非线性。
其函数原型如图：

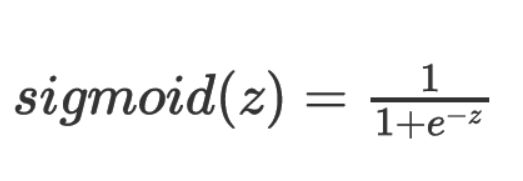
sigmoid函数的函数曲线以及其导数曲线如下图所示：

 Sigmoid的特点就是将输出映射到[0,1]之内，可以和概率轻易对应起来，很容易用来反映二分类结果的概率。事实上逻辑回归就是使用sigmoid函数作为输出概率的，后面可能会整理逻辑回归，同时谈一谈sigmoid和softmax的关系。但是显然sigmoid可以和类别概率对应起来，但是也仅仅能和二分类概率对应起来，对于多分类问题无能为力。
  另一个特点就是反向传播的计算比较简单，因为这个函数有一个特性，f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f’(x)，根据这个公式可以很快速的计算出反向传播的导数值。但是这个函数的计算本身就有点不容易，要计算指数还要计算除法。
  还有一点不足之处就是，这个函数由于具有软饱和性，训练的时候，对于绝对值较大的数，计算出来的梯度非常小，如果多层的梯度相乘，导致计算出来的最终梯度非常小，使得参数几乎无法更新，训练无法正常进行下去，这就是所谓的梯度消失问题。
  我们可以从函数图像很直观的看到，sigmoid函数是==不以0为中心的，==对所有的参数求导后，发现值是同正同负的，使得所有的参数更新时，只能朝一个方向，这样梯度下降的时候，下降的不够自由，就只能Z字形下降，会减慢收敛速度，具体的细节请大家自行研究。

当z的值从-∞向+∞过渡时，sigmoid函数的取值范围为(0, 1)，这正好是概率的取值范围，当z=0时，sigmoid(0)的值为0.5。因此，模型就可以将sigmoid的输出值 p 作为正例的概率，而 1-p 作为负例的概率。以阈值0.5作为两个分类的阈值，就是看 p 与 1-p 哪个类别的概率值更大，预测的结果就为哪个类别。

1、优点

1、 值域在0和1之间；

2 、 函数具有非常好的对称性。

3、sigmoid的优点在于输出范围有限，所以数据在传递的过程中不容易发散。当然也有相应的缺点，就是饱和的时候梯度太小。

4、求导容易。

2、缺点

见第四节

三、Tanh

Tanh的诞生比Sigmoid晚一些，sigmoid函数我们提到过有一个缺点就是输出不以0为中心，使得收敛变慢的问题。而Tanh则就是解决了这个问题。Tanh就是双曲正切函数。等于双曲余弦除双曲正弦。函数表达式和图像见下图。这个函数是一个奇函数。
双曲正切函数 ，简称 tanh，是一个形状类似的非线性激活函数，输出值介于-1.0和1.0之间。在20世纪90年代后期和21世纪初期，由于使用 tanh 函数的模型更容易训练，而且往往具有更好的预测性能，因此 tanh 函数比 Sigmoid激活函数更受青睐。
如图：

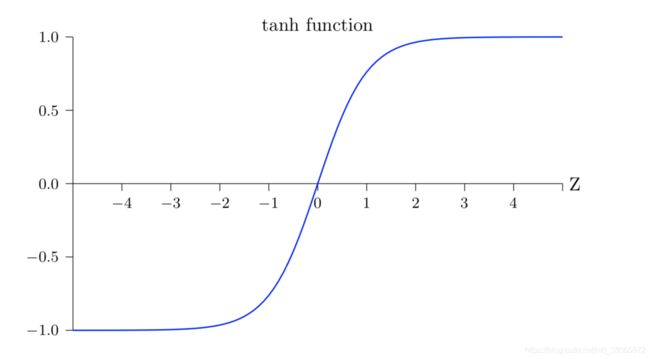
对tanh函数求导需要一定的数学基础，这里直接给出结果。tanh’(x)=1-tanh²(x)，这个函数同样是根据函数求导数很容易，但是函数值的计算比较复杂。

同样可以很轻易的证明这个函数两边趋于无穷极限是饱和的，函数图像和sigmoid函数非常像，其实就是直接在竖直方向拉伸两倍，然后在y轴向下平移了1个单位，使得函数的中心回到了0，然后在水平方向上拉伸两倍。tanh(x)=2sigmoid(2X)−1。解决了sigmoid函数收敛变慢的问题，相对于sigmoid提高了收敛速度。

其他特点都是类似的，根据函数值求导数值简单，但是指数的计算复杂。梯度消失的特点依旧保留，因为两边的饱和性使得梯度消失，进而难以训练。
  尽管tanh函数和sigmoid函数存在梯度消失的问题，但是与之类似，如果函数的梯度过大又会导致梯度爆炸的问题，显然tanh和sigmoid的导函数非常有界，根据导数公式，很容易得出tanh’(x)∈[0,1]，所以完全不用担心因为使用激活函数而产生梯度爆炸的问题。

四、Sigmoid 和 Tanh 激活函数的局限性

一个神经网络由层节点组成，并学习将输入的样本映射到输出。对于给定的节点，将输入乘以节点中的权重，并将其相加。此值称为节点的summed activation。然后，经过求和的激活通过一个激活函数转换并定义特定的输出或节点的“activation”。

最简单的激活函数被称为线性激活，其中根本没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练，但不能学习复杂的映射函数。线性激活函数仍然用于预测一个数量的网络的输出层(例如回归问题)。

非线性激活函数是更好的，因为它们允许节点在数据中学习更复杂的结构 。两个广泛使用的非线性激活函数是sigmoid 函数和双曲正切 激活函数。

**Sigmoid和 tanh 函数的一个普遍问题是它们值域饱和了 。**这意味着，大值突然变为1.0，小值突然变为 -1或0。此外，函数只对其输入中间点周围的变化非常敏感。

无论作为输入的节点所提供的求和激活是否包含有用信息，函数的灵敏度和饱和度都是有限的。一旦达到饱和状态，学习算法就需要不断调整权值以提高模型的性能。

最后，随着硬件能力的提高，通过 gpu 的非常深的神经网络使用Sigmoid 和 tanh 激活函数不容易训练。在大型网络深层使用这些非线性激活函数不能接收有用的梯度信息。错误通过网络传播回来，并用于更新权重。每增加一层，错误数量就会大大减少。这就是所谓的**消失梯度问题，**它能有效地阻止深层(多层)网络的学习。

虽然非线性激活函数的使用允许神经网络学习复杂的映射函数，但它们有效地阻止了学习算法与深度网络的工作。在2000年代后期和2010年代初期，通过使用诸如波尔兹曼机器和分层训练或无监督的预训练等替代网络类型，这才找到了解决办法

五、softmax（待补充）