【MATLAB】机器学习:线性判别分析LDA
实验内容
1.将LDA在训练样本上的低维表示结果可视化。
2.使用距离最短对测试样本进行分类。
实验代码
clear;clc;
%% 导入数据
load("train.mat");
x=train(:,1:4);
y=train(:,5);
load("test.mat");
x_test=test;
% *********************问题二*******************
% **********************************************
%% 训练样本的结果可视化
[mappedX,mapping]=lda(x,y,2);
% 训练样本中的第一等级
index1=find(y==1);
plot(mappedX(index1,1),mappedX(index1,2),'or','MarkerSize',15);
hold on;
% 训练样本中的第二等级
index2=find(y==2);
plot(mappedX(index2,1),mappedX(index2,2),'^g','MarkerSize',15);
hold on;
% 训练样本中的第三等级
index3=find(y==3);
plot(mappedX(index3,1),mappedX(index3,2),'sb','MarkerSize',15);
legend('训练样本中的第一等级','训练样本中的第二等级','训练样本中的第三等级');
hold on;
% ********************问题三********************
% **********************************************
%% 距离最短对测试样本进行分类
for i=1:size(x_test,1)
for j=1:size(x,1)
dist(i,j)=sqrt(sum((x_test(i,:)-x(j,:)).^2,2));
end
end
[min,index]=min(dist,[],2);
y_test=[y(index(1));y(index(2))];
%% 全部样本的可视化
X=[x;x_test];
Y=[y;y_test];
[mappedX,mapping]=lda(X,Y,2);
% 测试样本中的第一等级
temp1=find(Y==1);
ind1=find(temp1>size(x,1));
index1=temp1(ind1); % 全部样本中属于第一等级且为测试样本的索引
plot(mappedX(index1,1),mappedX(index1,2),'ok','MarkerSize',15);
hold on;
% 测试样本中的第二等级
temp2=find(Y==2);
ind2=find(temp2>size(x,1));
index2=temp2(ind2); % 全部样本中属于第二等级且为测试样本的索引
plot(mappedX(index2,1),mappedX(index2,2),'^k','MarkerSize',15);
hold on;
% 测试样本中的第三等级
temp3=find(Y==3);
ind3=find(temp3>size(x,1));
index3=temp3(ind3); % 全部样本中属于第三等级且为测试样本的索引
plot(mappedX(index3,1),mappedX(index3,2),'sb','MarkerSize',15);
其中,lda函数调用的lda.m代码文件如下
function [mappedX, mapping] = lda(X, labels, no_dims)
% 函数功能:使用LDA对数据集A进行降维至no_dims维
% 函数的参数:X(数据集)、labels(数据集X对应的标签)、no_dims(投影后的维度)
% 函数返回值:mappedX(投影后的no_dims维数据集)
% 步骤一:求均值
mapping.mean = mean(X, 1);
X = bsxfun(@minus, X, mapping.mean);
% 步骤二:求类内散度矩阵
[classes, bar, labels] = unique(labels);
nc = length(classes); % 确定标签的种类
Sw = zeros(size(X, 2), size(X, 2)); % 初始化Sw
St = cov(X); % 计算整体的协方差矩阵
for i=1:nc
cur_X = X(labels == i,:);
C = cov(cur_X);
p = size(cur_X, 1) / (length(labels) - 1);
Sw = Sw + (p * C);
end
% 步骤三:计算类间散度矩阵
Sb = St - Sw;
Sb(isnan(Sb)) = 0;
Sw(isnan(Sw)) = 0;
Sb(isinf(Sb)) = 0;
Sw(isinf(Sw)) = 0;
if nc <= no_dims
no_dims = nc - 1;
warning(['Target dimensionality reduced to ' num2str(no_dims) '.']); % 确保不要映射到较高维度
end
% 步骤四:求最大特征矩阵和特征向量
[M, lambda] = eig(Sb, Sw);
lambda(isnan(lambda)) = 0;
[lambda, ind] = sort(diag(lambda), 'descend');
M = M(:,ind(1:min([no_dims size(M, 2)])));
% 步骤五:计算投影数据
mappedX = X * M;
mapping.M = M;
mapping.val = lambda;
end
实验结果
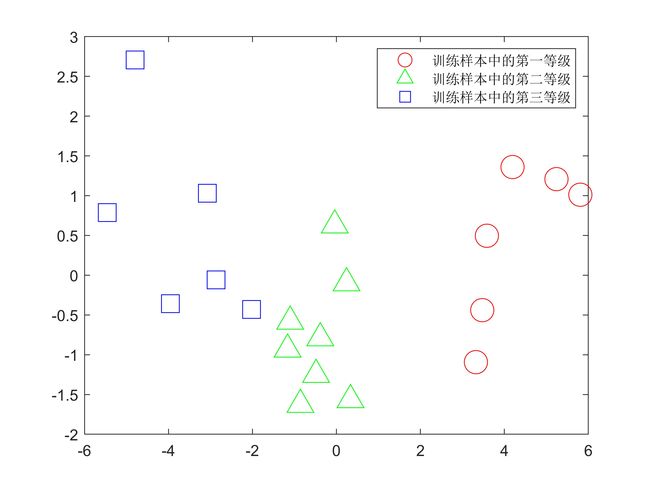

实验心得
通过本次“线性判别分析实验”的课上和课下学习,我对LDA这种有监督的数据降维方法有了更加深刻的理解:将带有标签的数据降维,投影到低维空间同时满足三个条件:①尽可能多地保留数据样本的信息(即选择最大的特征是对应的特征向量所代表的方向)。②寻找使样本尽可能好分的最佳投影方向。③投影后使得同类样本尽可能近,不同类样本尽可能远。