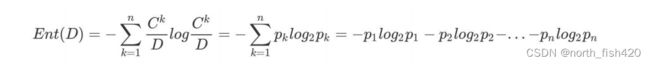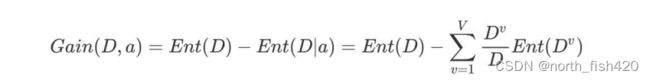回归:目标变量是数值型,得到方程式
分类:目标变量是分类值,可能是一个数,贝叶斯网络概率,神经网络,超平面函数
1理解模型
测量精度
基尼系数
1.1衡量指标
1.1.1熵
混杂样本中,熵是混乱程度的量度,样本集合纯度

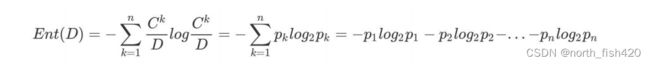
当数据量⼀致时,系统越有序,熵值越低;系统越混乱或者分散,熵值越⾼。

决策树目的:找到一个特征值,对其进行分类,然后使得纯度更高
1.1.2信息增益
信息增益: 以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越⼤,样本的不确定性就越⼤。
因此可以 使⽤划分前后集合熵的差值来衡量使⽤当前特征对于样本集合 D 划分效果的好坏 。
信息增益 = entroy( 前 ) - entroy( 后 )
父集的熵减去子集熵值的加权和
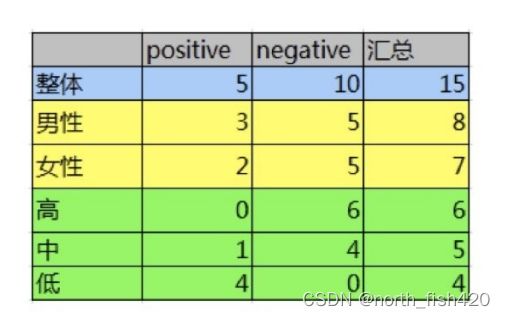
例子:

2模型训练
2.1数据集划分
三个方法:留出法、交叉验证法、自助法

2.2代码实现

3模型评估
【补充】
实证研究,一般用回归,追求影响因素,以及影响程度,只需要知道是否影响,影响程度
机器学习,判定预测的好,分为训练集和测试集,用训练集评估好,用测试集测精度
机器学习重点是评估、提高精度
经验误差:在训练集中模型的误差
泛化误差:在测试集中模型的误差
3.1过拟合与欠拟合
3.1.1定义
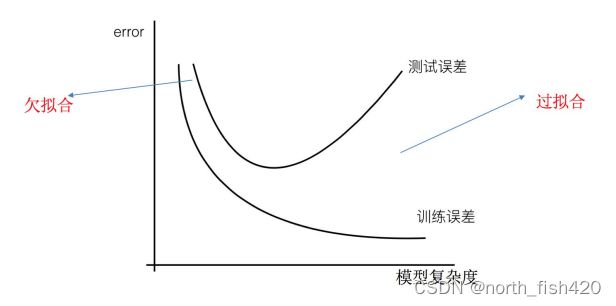
过拟合:⼀个假设 在训练数据上能够获得⽐其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据 , 此时认为这个假设出现了过拟合的现象。( 模型过于复杂 )
⽋拟合:⼀个假设 在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据 ,此时认为这个
假设出现了⽋拟合的现象。 ( 模型过于简单 )
3.1.2原因及解决方法
(1)⽋拟合
原因:学习到数据的特征过少
解决办法:
1 )添加其他特征项, 有时候我们模型出现⽋拟合的时候是因为特征项不够导致的,可以添加其他特征项来很好地解决。例如,“组合”、“泛化”、“相关性”三类特征是特征添加的重要⼿段,⽆论在什么场景,都可以照葫芦画瓢,总会得到意想不到的效果。除上⾯的特征之外,“上下⽂特征”、“平台特征”等等,都可以 作为特征添加的⾸选项。
2 )添加多项式特征 ,这个在机器学习算法⾥⾯⽤的很普遍,例如将线性模型通过添加⼆次项或者三次项 使模型泛化能⼒更强。
(2)过拟合
原因:原始特征过多,存在⼀些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法:
1 )重新清洗数据,导致过拟合的⼀个原因也有可能是数据不纯导致的,如果出现了过拟合就需要我们重 新清洗数据。
2 )增⼤数据的训练量,还有⼀个原因就是我们⽤于训练的数据量太⼩导致的,训练数据占总数据的⽐例 过⼩。
3 )正则化
4 )减少特征维度,防⽌ 维灾难
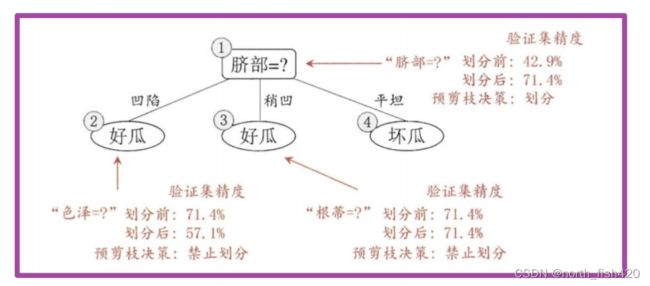
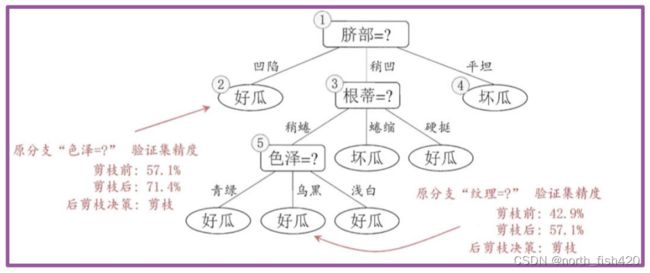
5)剪枝策略
在决策树学习中,为了尽可能正确分类训练样本,结点划分过程将不断重复,有时会造成决策树分⽀过多,这时就可能 因训练样本学得" 太好 " 了,以致于把训练集⾃身的⼀些特点当作所有数据都具有的⼀般性质⽽导致过拟合。因此,可通 过主动去掉⼀些分⽀来降低过拟合的⻛险 。
预剪枝:限制深度,时间短
后剪枝:通过加入惩罚,叶子节点越多,损失越大
后剪枝决策树通常⽐预剪枝决策树保留了更多的分⽀。
⼀般情形下,后剪枝决策树的⽋拟合⻛险很⼩,泛化性能往往优于预剪枝决策树。 但后剪枝过程是在⽣成完全决策树之后进⾏的。 并且要⾃底向上地对树中的所有⾮叶结点进⾏逐⼀考察,因此其 训练时间开销⽐未剪枝决策树和预剪枝决策树都要⼤得多.
3.2精度与召回率
3.2.1混淆矩阵
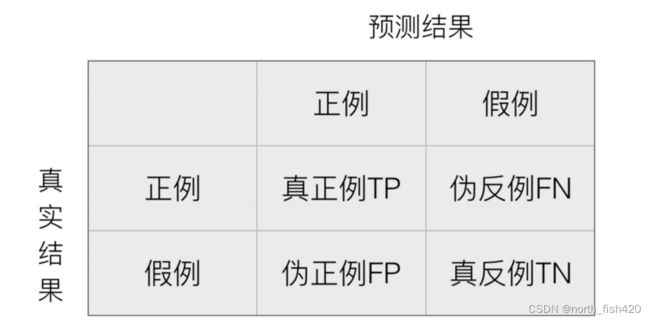
精确率:预测结果为正例样本中真实为正例的⽐例(了解)

召回率:真实为正例的样本中预测结果为正例的⽐例(查得全,对正样本的区分能⼒)

计算举例: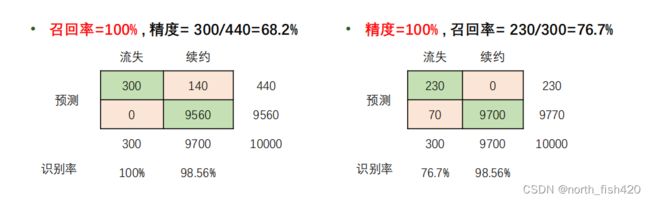
性能指标如下:


3.3ROC与AUC曲线
(32条消息) 5分钟带你学懂ROC曲线_最强理发师托尼的博客-CSDN博客_roc图
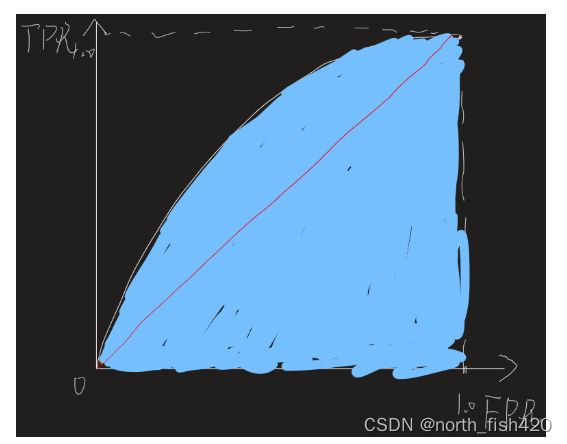
ROC曲线是TPR与FPR的函数曲线
首先,对于一个特定的学习器(模型)和一个样本,在坐标上有且仅对应一个点(一组结果),那么我们怎样得到一系列结果从而生成一个“平滑”的ROC曲线呢?
我们测试集有n个样本就可以说生成对应的点(n组结果),从而生成一个“平滑”的ROC曲线。
学习器(分类器)可以帮助我们生成预测该样本是正样本的概率,有n个样本就生成n个score值,放入列表中,将其从大到小排序,依次将各score值从大到小顺序设置为阈值(threshold),只要样本score值大于等于当前阈值则认为是正样本、否则认为是负样本。即每个阈值对应一个混淆矩阵,得到一组结果。以此类推,我们可以得到n组结果,并将其连成平滑曲线。
ROC 曲线的横轴就是 FPRate ,纵轴就是 TPRate ,当⼆者相等时,表示的意义则是:对于不论真实类别是 1 还是 0 的 样本,分类器预测为1 的概率是相等的,此时 AUC 为 0.5
AUC表示ROC曲线下面积

ROC曲线有一个很好的特点:在总样本中正负样本比例变化的情况下,ROC曲线能够保持很小的变化/甚至不变(证明思路是会用所有样本的threshold生成结果,样本数目足够大时,最终生成稳定曲线,笔者这里没有详细证明)。这在很多工程问题上有较好的体现,例如在新冠疫情病毒检测中,正样本数目一定远远大于负样本数目,这就体现了ROC与AUC模型泛化性能评价体系的优势。
4拓展--modeler软件