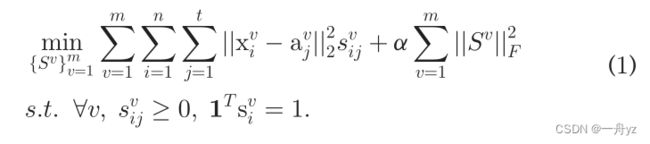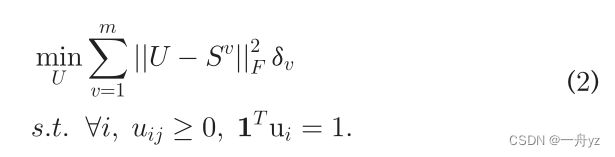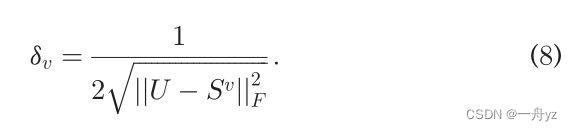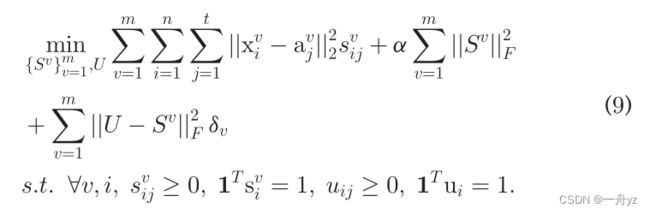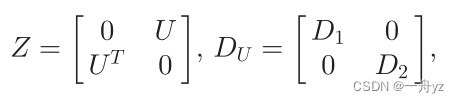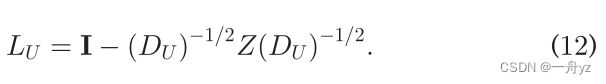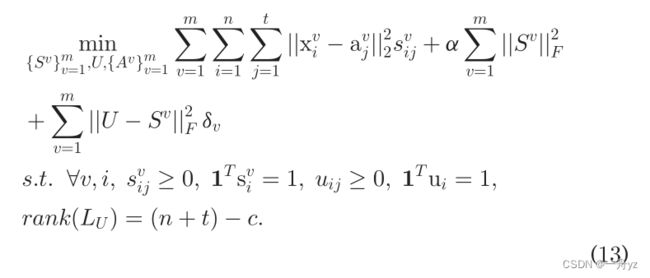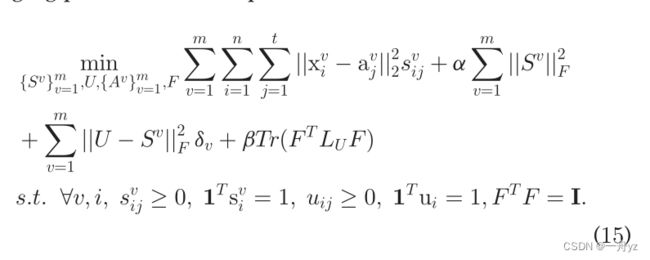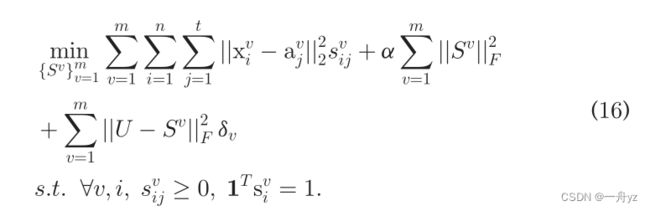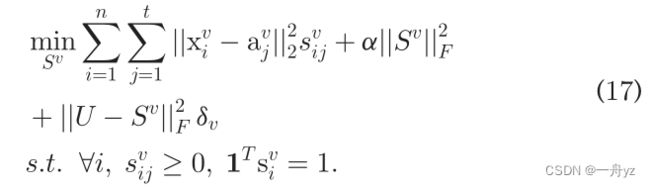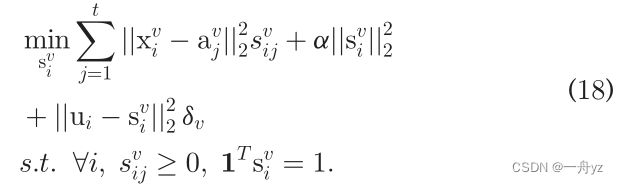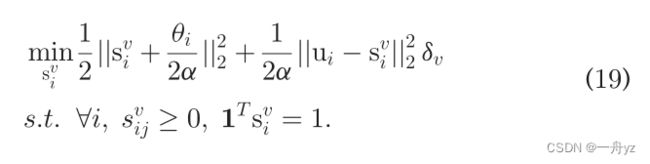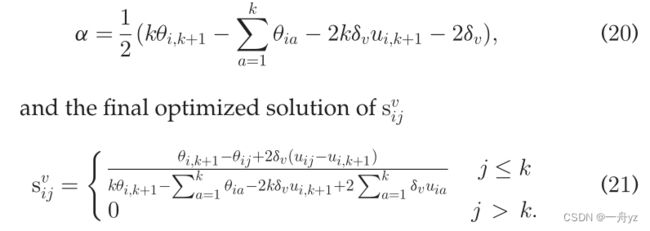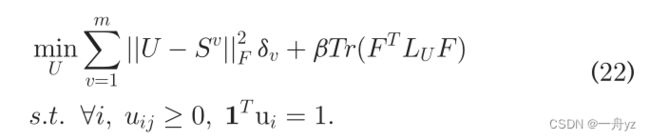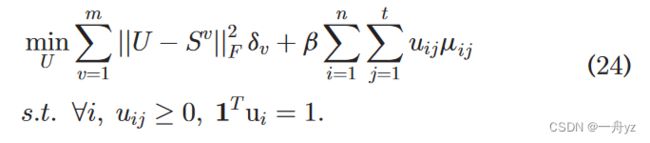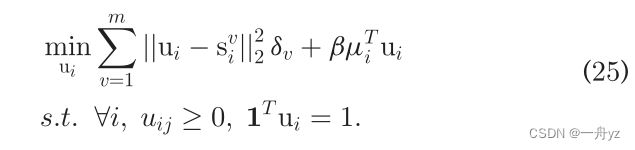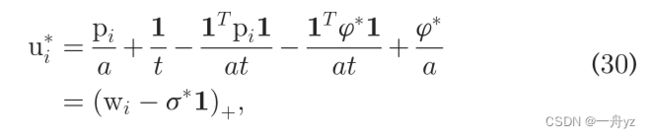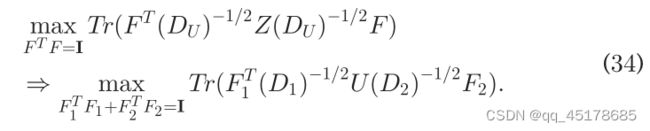Bipartite Graph Based Multi-View Clustering

Bipartite Graph Based Multi-View Clustering

基于二部图的多视图聚类

abstract

对于基于图的多视图聚类，一个关键问题是通过两阶段学习方案捕获共识聚类结构。具体来说，首先学习多个视图的相似性图矩阵，然后将它们融合为统一的高级图矩阵。大多数当前的方法独立地学习每个视图的数据点之间的成对相似性，这在单个视图中被广泛使用。然而，包含在多个视图中的共识信息被忽略，并且所涉及的偏差导致不期望的统一图矩阵。为此，我们提出了一种基于二分图的多视图聚类（BIGMC）方法。共识信息可以由不同视图的少量代表性统一锚点表示。在数据点和锚点之间构建二分图。BIGMC构建所有视图的二分图矩阵，并将其融合以生成统一的二分矩阵。统一的二分图矩阵进而改进每个视图的二分图形相似性矩阵并更新锚点。最终的统一图矩阵直接形成最终的簇。在BIGMC中，为每个视图添加自适应权重以避免异常视图。对统一矩阵的拉普拉斯矩阵施加低秩约束，以构造多分量统一二分图。

introduction

基于图的多视图聚类方法旨在通过组合所有视图的图矩阵，以统一的图矩阵的形式对数据对象之间的相似关系进行编码。通过在统一图矩阵上使用附加的聚类方法来形成最终聚类。聚类性能取决于每个视图图的质量和融合策略。

• 在学习每个视图图矩阵时，不考虑不同视图的共识信息。大多数现有方法独立地学习每个视图的对象之间的成对相似性。这通常导致所涉及的偏差影响每个视图图矩阵的质量。我们的方法通过学习不同视图的少量代表性统一锚点来获取共识信息。每个视图都有一个锚点集，不同视图中的这些锚点将信息保存在相同的子集群中
• 第二，他们在融合过程中保持预先给定的锚点集和学习的视图图矩阵固定不变，在这种情况下，它们对初始化很敏感，很容易陷入局部最优。我们的方法以相互增强的方式共同学习每个视图二分图矩阵、统一图矩阵和统一锚点。他们可以相互学习。
• 第三，如果没有附加的超参数，大多数方法无法自适应地学习每个视图的权重。额外超参数的最佳值需要在大范围内搜索。我们的方法可以基于相应的学习视图二分图和统一的图矩阵自适应地确定每个视图的最优权重。

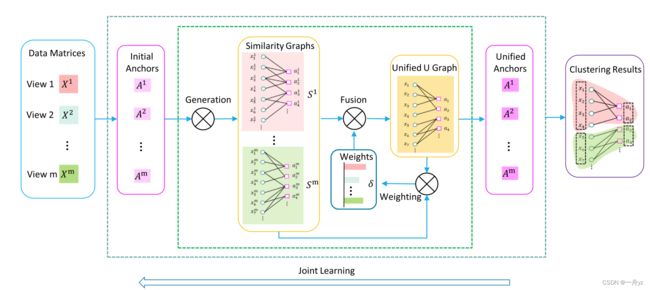
为了解决这些问题，提出了BIGMC,总体架构图：

1. 从多视图数据矩阵的输入中，为不同视图创建t个初始统一锚点，记为A。
2. 然后根据数据点与锚点的相似度生成各个视图的图，称为“数据到锚点”的相似度图，记为S。
3. 然后利用来自多个视图的所有Ss，在融合过程中学习一个统一的图矩阵U。同时，每个视图 （$\delta$） i s 的权重基于 Ss 和 U 自适应地添加，表明其重要性。添加秩约束。
4. 接下来，得到的统一矩阵U将返回，改进每个视图的Ss和$\delta$，直到收敛。
5. 根据收敛的统一图矩阵U，我们可以得到每个视图的统一锚点A。如果它们与初始锚点不同，我们将改进所有As，以依次更新Ss、统一图矩阵U和权重d，直到它们相同。最终的簇是基于U直接形成的。

本文贡献：

• 我们提出了一种新的基于二部图的多视图聚类方法。BIGMC可以学习和利用由少量统一锚点所代表的共识信息，减轻了多个视图中包含的偏见的影响。
• BIGMC共同学习每个视图的相似二部图、统一二部图、共识锚，相互强化。它还可以自动确定每个二部图的权重，而不引入附加超参数。当不同视图中的锚点相同时，直接根据统一的二部图生成最终的聚类。
• BIGMC采用高效的交替迭代优化策略，逐级求解变量优化问题，每个子问题都有一个最优解。
• 在合成数据集和真实数据集上的实验结果证明了所提出的BIGMC的有效性和比现有基线的优越性。

PROPOSED METHOD

$X\in R^{d\times n}$

$l_p$范式定义为：$||x|{|}_p=({\sum }_{i=1}^d|x_i{|}^p{)}^{1/p}$

对于有m个视图的多视图数据集，我们表示$X^1,X^2,\dots ,X^m$作为数据矩阵 $X^v=[x_1^v,\dots ,x_n^v]R^{d_v\times n}$作为具有$d_v$维数和n个数据点的第v个视图数据。

对于$X^v$，设$x_j^v$是第j个列向量，$X_{ij}^v$是第（i,j）个条目 $A^v=[a_1^v,\dots ,a_t^v]\in R^{d_v\times t}$

值得注意的是，所有视图数据都有t个共识锚点，其中每个锚点都是相应子聚类的质心。当t = c时，每个集群只有一个锚点

View Graph Learning

$S^v\in R^{n\times t}$

在这里，我们通过在固定锚集时为每个视图构建相似度矩阵来独立学习视图图。原因是每个图只通过锚点集彼此关联。

然后，我们生成一个统一的二部图矩阵，并利用它自适应更新$\{A^v{\}}_{v=1}^m$直到收敛。

Unified Graph Learning

我们提出的BIGMC可以联合学习所有视图的图，构造一个统一的二部图，并自动确定每个视图的重要性。

具体来说，通过$\{S^v{\}}_{v=1}^m$的统一矩阵$U\in R^{n\times t}$可以得到统一的二部图。

权重公式：

来源：https://blog.csdn.net/qq_45178685/article/details/127976977

结合问题1 2 来联合学习$S^{v}U$:

我们注意到，当A是固定的时候，矩阵S和U可以在一个问题中联合学习。在下一小节中，我们可以自适应地找到所有视图的共识锚点

Consensus Anchor Learning

当统一矩阵U更新时，我们可以探索共识锚，并在所有视图中重新定位它们。对于第v个视图数据的第j个子簇，根据与之连接的所有数据点的平均值可以得到它的锚点$a_j^v$

其中$a_j^v\in R^{d_v\times 1}j=1,\dots ,t$

Optimal Bipartite Graph Learning

二部图的边权可以用U表示 其中每个元素$u_{ij}$是连接$x_i$和所有视图对应的$a_j$的边的权值

在这种情况下，加权邻接矩阵 $Z\in R^{(n+t)\times (n+t)}$ 度矩阵$D_U$

$D_1\in R^{n\times n},其中的元素是{\sum }_{j=1}^t{u}_{ij},D_2\in R^{t\times t}其中的元素是{\sum }_{i=1}^n{u}_{ij}$

归一化的矩阵：

引理二：归一化拉普拉斯矩阵LU的特征值0的重数c等于与U相关的二部图中连通分量的个数。

问题进一步转化为：

OPTIMIZATION STRATEGY

迭代优化

固定$\{{\delta }_v{\}}_{v=1}^m$U、F,$\{A_v{\}}_{v=1}^m$ 更新S

问题变为：

所有视图间是独立的：

此外，我们还可以发现对每个向量更新$s_i^v$是独立的:

简化计算：${\theta }_i的第j个元素是{\theta }_{ij}=||x_i^v-a_j^v||$ 问题18变为：

推导过程：
$$\begin{array}{rl}& \min \sum _{j=1}^t{\Vert x_i^v-a_j^v\Vert }_2^2{s}_{ij}^v+\alpha {\Vert s_i^v\Vert }_2^2+{\Vert u_i-s_i^v\Vert }_2^2{\delta }_v\\ & \min \sum _{j=1}^t{\theta }_{ij}{s}_{ij}^v+\alpha {\Vert s_i^v\Vert }_2^2+{\Vert u_i-s_i^v\Vert }_2^2{\delta }_v\\ & \min \sum _{i=1}^t\sum _{j=1}^t{\theta }_{ij}{s}_{ij}^v+\alpha {\Vert s^v\Vert }_F^2+{\Vert U-S^v\Vert }_F^2{\delta }_v\\ & \min \sum _{i=1}^t{\theta }_i^T{s}_i^v+\alpha {s_i^v}^T{s}_i^v+{\Vert u_i-s_i^v\Vert }_2^2{\delta }_v\\ & \min \sum _{i=1}^t\frac{{\theta }_i^T{s}_2^v}{\alpha }+{s_i^v}^T{s}_i^v+\frac{{\Vert u_i-s_i^v\Vert }_2^2}{\alpha }{\delta }_v\\ & \min \sum _{i=1}^t{s_i^v}^T{s}_i^v+\frac{2{\theta }_i^T{s}_i^v}{2\alpha }+\frac{{\theta }_i^T\theta }{4{\alpha }^2}-\frac{{\theta }_i^T\theta }{4{\alpha }^2}+\frac{{\Vert u_i-s_i^v\Vert }_2^2}{\alpha }\delta v\\ & \min \sum _{i=1}^t{\Vert s_i^v+\frac{{\theta }_i}{2\alpha }\Vert }_2^2+\frac{1}{\alpha }{\Vert u_i^v-s_i^v\Vert }_2^2{\delta }_v\end{array}$$
如果我们约束svi有k个非零元素，问题(19)可以用闭合形式来解决。也就是说，对于每个数据点xv i，只考虑k个最近的锚，而不是k个最近的数据点。

根据GMC:https://blog.csdn.net/qq_45178685/article/details/127976977

固定$\{S_v{\}}_{v=1}^m$、U、F、$\{A_v{\}}_{v=1}^m$ 更新 $\{{\delta }_v{\}}_{v=1}^m$

问题变为问题2 由等式8求解

固定$\{S_v{\}}_{v=1}^m$、$\{{\delta }_v{\}}_{v=1}^m$、F、$\{A_v{\}}_{v=1}^m$ 更新 U

问题变为：

归一化拉普拉斯矩阵的性质：

问题22变为：

类似地，为U中的每一行更新ui是独立的。我们可以有:

根据拉格朗日函数：

固定$\{S_v{\}}_{v=1}^m$、U、$\{{\delta }_v{\}}_{v=1}^m$、$\{A_v{\}}_{v=1}^m$ 更新 F

问题变为：

F写成分块矩阵形式：

$F_1\in R^{n\times c}{F}_2\in R^{t\times c}$

问题变为：

令$B=(D_1{)}^{-1/2}U(D_2{)}^{-1/2}B\in R^{n\times t}$