sklearn初探（七）：DBSCAN算法聚类及可视化

sklearn初探（七）：DBSCAN算法聚类及可视化

前言

本次任务采用DBSCAN算法对青蛙叫声的MFCC文件进行聚类分析，使用f-m指数与调整后兰德指数进行评分与调参，使用t-sne对聚类结果进行降维，使用matplotlib将结果可视化。数据集链接及完整源代码见文末。

概述

DBSCAN算法

The DBSCAN 算法将簇视为被低密度区域分隔的高密度区域。由于这个相当普遍的观点， DBSCAN发现的簇可以是任何形状的，与假设簇是凸的 K-means 相反。 DBSCAN 的核心概念是 core samples, 是指位于高密度区域的样本。 因此一个簇是一组核心样本，每个核心样本彼此靠近（通过某个距离度量测量） 和一组接近核心样本的非核心样本（但本身不是核心样本）。算法中的两个参数, min_samples 和 eps,正式的定义了我们所说的 稠密（dense）。较高的 min_samples 或者较低的 eps 都表示形成簇所需的较高密度。
更正式的,我们定义核心样本是指数据集中的一个样本的 eps 距离范围内，存在 min_samples 个其他样本，这些样本被定为为核心样本的邻居( neighbors) 。这告诉我们，核心样本在向量空间的稠密区域。一个簇是一个核心样本的集合，可以通过递归来构建，选取一个核心样本，查找它所有的邻居样本中的核心样本，然后查找新获取的核心样本的邻居样本中的核心样本，递归这个过程。 簇中还具有一组非核心样本，它们是簇中核心样本的邻居的样本，但本身并不是核心样本。 显然，这些样本位于簇的边缘。
当参数min_samples 主要表示算法对噪声的容忍度(当处理大型噪声数据集时, 需要考虑增加该参数的值), 针对具体地数据集和距离函数，参数eps 如何进行合适地取值是非常关键，这通常不能使用默认值。参数eps控制了点地领域范围。如果取值太小,大部分地数据并不会被聚类(被标注为 -1 代表噪声); 如果取值太大，可能会 导致 相近 的多个簇被合并成一个,甚至整个数据集都被分配到一个簇。
注意，与k-means聚类不同的是，使用DBSCAN并不能确定结果中聚类的数量，这意味着我们要自己调参。

调整后兰德指数

在已知真实簇标签分配(the ground truth class assignment) labels_true 和我们的聚类算法基于相同样本所得到的 labels_pred，调整后的兰德指数(adjusted Rand index) 是一个函数，用于测量两个簇标签分配的值的 相似度 ，忽略排列(permutations)和 with chance normalization:

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)  
0.24...

在预测的标签列表中重新排列 0 和 1, 把 2 重命名为 3, 得到相同的得分:

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)  
0.24...

另外， adjusted_rand_score 是 对称的(symmetric) : 交换参数不会改变得分。它可以作为 共识度量(consensus measure):

>>> metrics.adjusted_rand_score(labels_pred, labels_true)  
0.24...

完美的标签的得分为 1.0。

fowlkes-mallows指数

当样本的已标定的真实类分配已知时，可以使用 Fowlkes-Mallows 指数 (sklearn.metrics.fowlkes_mallows_score) 。Fowlkes-Mallows 得分 FMI 被定义为 成对的准确率和召回率的几何平均值:

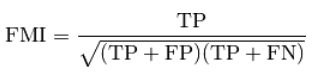
其中的 TP 是 真正例(True Positive) 的数量（即，真实标签组和预测标签组中属于相同簇的点对数），FP 是 假正例(False Positive) （即，在真实标签组中属于同一簇的点对数，而不在预测标签组中），FN 是 假负例(False Negative) 的数量（即，预测标签组中属于同一簇的点对数，而不在真实标签组中）。
得分范围为 0 到 1。较高的值表示两个簇之间的良好相似性。

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)  
0.47140...

在预测的标签列表中重新排列 0 和 1, 把 2 重命名为 3, 得到相同的得分:

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)  
0.47140...

完美的标签得分是 1.0。

数据分割

import pandas as pd

frog_data = pd.read_csv("../datas/Frogs_MFCCs.csv")
tLabel = []
for family in frog_data['Family']:
    if family == "Leptodactylidae":
        tLabel.append(0)
    elif family == "Dendrobatidae":
        tLabel.append(1)
    elif family == "Hylidae":
        tLabel.append(2)
    else:
        tLabel.append(3)
first_set = frog_data[['MFCCs_ 1', 'MFCCs_ 5', 'MFCCs_ 9', 'MFCCs_13', 'MFCCs_17', 'MFCCs_21']]

second_set = frog_data[['MFCCs_ 3', 'MFCCs_ 7', 'MFCCs_11', 'MFCCs_15', 'MFCCs_19']]

DBSCAN处理

fit一下。

db = cluster.DBSCAN(eps=0.1011, min_samples=115, n_jobs=-1)
db.fit(first_set)
r = pd.concat([first_set, pd.Series(db.labels_, index=first_set.index)], axis=1)
r.columns = list(first_set.columns) + [u'聚类类别']
# print(r)
r.to_excel("../output/dbscanSet_1.xlsx")

调参

dbscan需要我们调参。本次任务需要调参以达到这样的效果：聚类结果为四类，且评分尽量高。

Set1

eps	min_samples	聚类数量	fowlkes-mallows得分
0.1	150	4	0.6762988391651638
0.1	175	4	0.6712206459932587
0.1	200	3	-
0.1	125	4	0.6813089522934992
0.1	120	4	0.6815870169183239
0.1	130	4	0.6805885740745339
0.1	115	4	0.6830254509032943
0.1	110	5	-
0.09	115	4	0.6642916488855524
0.11	115	6	-
0.095	115	4	0.6748581101560627
0.105	115	5	-
0.101	115	4	0.6848332275397843
0.102	115	5	-
0.1015	115	5	-
0.1011	115	4	0.6849251120786362

Set2

eps	min_samples	聚类数量	fowlkes-mallows得分
0.1	115	4	0.6674327901587477
0.1	120	4	0.6672727687106378
0.1	110	4	0.6690055278219934
0.1	105	4	0.6700344543118204
0.1	100	4	0.6720072870174673
0.1	95	4	0.6729892684302224
0.1	90	4	0.6734227611274493
0.1	85	5	-
0.105	90	5	-
0.101	90	4	0.6743460020206788
0.102	90	4	0.6759196726408404
0.103	90	5	-
0.1025	90	5	-
0.1021	90	4	0.6759196726408404
0.1022	90	5	-

t-sne降维

t_sne_db_1 = TSNE()
t_sne_db_1.fit(first_set)
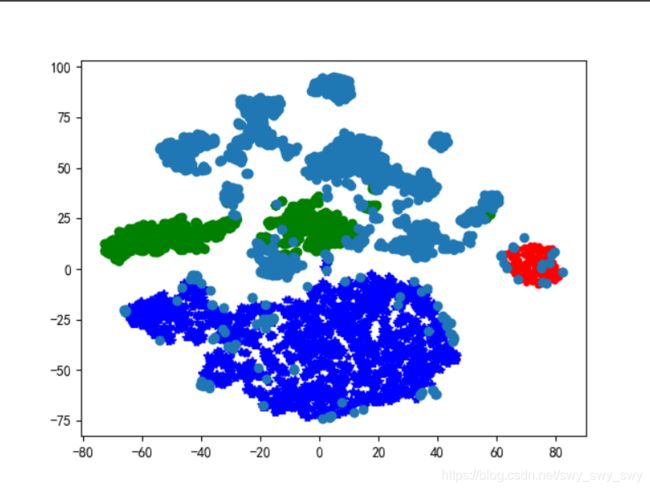
t_sne_db_1 = pd.DataFrame(t_sne_db_1.embedding_, index=first_set.index)

可视化

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
dd = t_sne_db_1[r[u'聚类类别'] == 0]
plt.plot(dd[0], dd[1], 'r.')
dd = t_sne_db_1[r[u'聚类类别'] == 1]
plt.plot(dd[0], dd[1], 'go')
dd = t_sne_db_1[r[u'聚类类别'] == 2]
plt.plot(dd[0], dd[1], 'b*')
dd = t_sne_db_1[r[u'聚类类别'] == -1]
plt.plot(dd[0], dd[1], 'o')
plt.savefig("../output/dbscanSet_1.png")
plt.clf()

效果如下：

源代码

这里就只放一个训练集的吧，我没做封装。

import pandas as pd
from sklearn import cluster
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

frog_data = pd.read_csv("../datas/Frogs_MFCCs.csv")
tLabel = []
for family in frog_data['Family']:
    if family == "Leptodactylidae":
        tLabel.append(0)
    elif family == "Dendrobatidae":
        tLabel.append(1)
    elif family == "Hylidae":
        tLabel.append(2)
    else:
        tLabel.append(3)

first_set = frog_data[['MFCCs_ 1', 'MFCCs_ 5', 'MFCCs_ 9', 'MFCCs_13', 'MFCCs_17', 'MFCCs_21']]

second_set = frog_data[['MFCCs_ 3', 'MFCCs_ 7', 'MFCCs_11', 'MFCCs_15', 'MFCCs_19']]

# DBSCAN begins
db = cluster.DBSCAN(eps=0.1011, min_samples=115, n_jobs=-1)
db.fit(first_set)
r = pd.concat([first_set, pd.Series(db.labels_, index=first_set.index)], axis=1)
r.columns = list(first_set.columns) + [u'聚类类别']
# print(r)
r.to_excel("../output/dbscanSet_1.xlsx")
p_labels = list(db.labels_)
with open(scoreFile, "a") as sf:
    sf.write("By DBSCAN, the f-m_score of Set_1 is: " + str(
        metrics.fowlkes_mallows_score(tLabel, p_labels)) + "\n")
    sf.write("By DBSCAN, the rand_score of Set_1 is: " + str(
        metrics.adjusted_rand_score(tLabel, p_labels)) + "\n")

t_sne_db_1 = TSNE()
t_sne_db_1.fit(first_set)
t_sne_db_1 = pd.DataFrame(t_sne_db_1.embedding_, index=first_set.index)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
dd = t_sne_db_1[r[u'聚类类别'] == 0]
plt.plot(dd[0], dd[1], 'r.')
dd = t_sne_db_1[r[u'聚类类别'] == 1]
plt.plot(dd[0], dd[1], 'go')
dd = t_sne_db_1[r[u'聚类类别'] == 2]
plt.plot(dd[0], dd[1], 'b*')
dd = t_sne_db_1[r[u'聚类类别'] == -1]
plt.plot(dd[0], dd[1], 'o')
plt.savefig("../output/dbscanSet_1.png")
plt.clf()

数据集

https://download.csdn.net/download/swy_swy_swy/12409033