机器学习-决策树(Decision Tree)进阶篇之剪枝
此篇博客对决策树的剪枝做展开了解,对决策树还不了解的读者可以先读我的上一篇博客机器学习-决策树(Decision Tree)基础篇![]() https://blog.csdn.net/m0_52053228/article/details/127839854?spm=1001.2014.3001.5501
https://blog.csdn.net/m0_52053228/article/details/127839854?spm=1001.2014.3001.5501
此篇博客我将拿西瓜书中的数据以及我自己的数据来做决策树的剪枝。
目录
一、剪枝
1-1、什么是过拟合
1-2、基本策略
二、预剪枝
2-1、西瓜书数据2.0实现预剪枝
2-2、用自己的数据实现预剪枝
三、后剪枝
3-1、西瓜书数据2.0实现后剪枝
3-2、用自己的数据实现后剪枝
四、整体代码
五、总结
一、剪枝
剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段。
1-1、什么是过拟合
过拟合(over-fitting)是指模型在训练集上表现很好,到了验证和测试阶段就很差,即模型的泛化能力很差。
举个例子讲就是当我需要建立好一个模型之后,比如是识别一只狗狗的模型,我需要对这个模型进行训练。恰好,我训练样本中的所有训练图片都是二哈,那么经过多次迭代训练之后,模型训练好了,并且在训练集中表现得很好,给定一个二哈的测试样本都能正确的预测结果。基本上二哈身上的所有特点都涵括进去,那么问题来了!假如我的测试样本是一只金毛呢?将一只金毛的测试样本放进这个识别狗狗的模型中,很有可能模型最后输出的结果不是一条狗(因为这个模型基本上是按照二哈的特征去打造的,这个模型太贴合二哈,对二哈的识别率非常高,反而导致泛化能力比较差)。所以这样就造成了模型过拟合,虽然在训练集上表现得很好,但是在测试集中表现得恰好相反,在性能的角度上讲就是协方差过大(variance is large),同样在测试集上的损失函数(cost function)会表现得很大。
1-2、基本策略
决策树剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(postpruning)。
- 预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点得划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点
- 后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
二、预剪枝
2-1、西瓜书数据2.0实现预剪枝
我们先拿西瓜书的数据来看一下预剪枝是如何进行的。
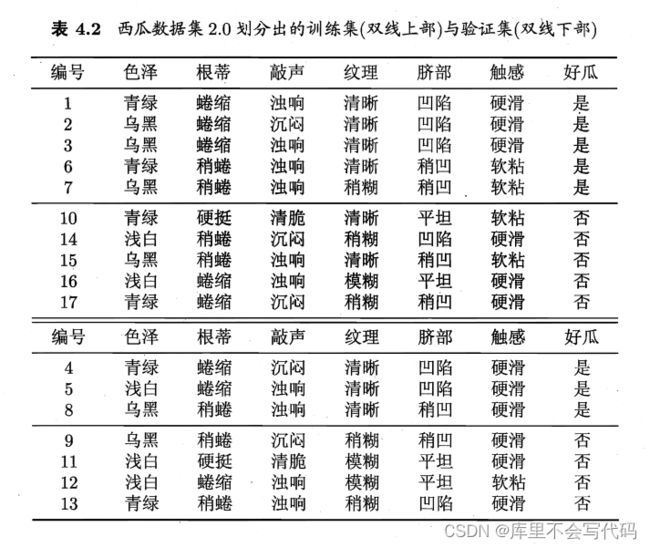
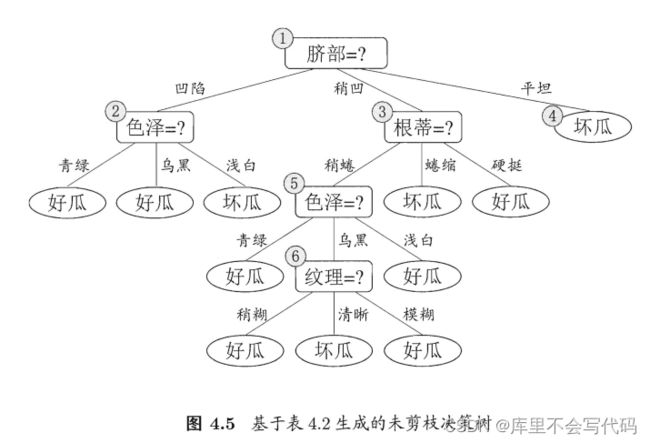
下面是西瓜书中给出的数据集以及根据信息增构造出的一颗未剪枝的决策树
因为是预剪枝,所以要判断是否应该进行这个划分。
判断的标准就是看划分前后的泛华性能是否有提升,也就是如果划分后泛华性能有提升,则划分;否则,不划分。
下面来看看是否要用脐部进行划分。
- 划分前:所有样例集中在根结点,若不进行划分,该结点将被标记为叶结点,其类别标记为训练样例数最多的类别,假设我们将这个叶结点标记为“好瓜”。用验证集对这个单结点决策树进行评估,则编号为{4,5,8}的样例被分类正确,另外4个样例分类错误,于是,验证集精度为
- 划分后:图4.6中的结点②、③、④分别包含编号为{1,2,3,14}、{6,7,15,17}、{10,16}的训练样例,因此这3个结点分别被标记为叶结点“好瓜”、“好瓜”、“坏瓜”。此时,验证集中编号为{4,5,8,11,12}的样例被分类正确,验证集精度为

![]() ,即划分后精度大于划分前精度,于是用“脐部”进行划分得以确定。
,即划分后精度大于划分前精度,于是用“脐部”进行划分得以确定。
接下来,决策树算法对结点②进行划分,再次使用信息增益挑选出值最大的那个特征,这里我就不算了,计算方法和上面类似。以此类推,就可以得出预剪枝之后的决策树。
下面我们通过python来实现预剪枝
# 创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):
trainData = np.asarray(dataTrain)
labelTrain = np.asarray(labelTrain)
testData = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labelTrain)) == 1:
return labelTrain[0]
# 如果没有待分类特征
elif trainData.size == 0:
return voteLabel(labelTrain)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据最优特征进行分割
dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)
# 预剪枝评估
# 划分前的分类标签
labelTrainLabelPre = voteLabel(labelTrain)
labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size
# 划分后的精度计算
if dataTest is not None:
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)
# 划分前的测试标签正确比例
labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size
# 划分后 每个特征值的分类标签正确的数量
labelTrainEqNumPost = 0
for val in labelTrainSet.keys():
labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0
# 划分后 正确的比例
labelTestRatioPost = labelTrainEqNumPost / labelTest.size
# 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
if dataTest is None and labelTrainRatioPre == 0.5:
decisionTree = {bestFeatName: {}}
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, None, None, names, method)
elif dataTest is None:
return labelTrainLabelPre
# 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
elif labelTestRatioPost < labelTestRatioPre:
return labelTrainLabelPre
else :
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, dataTestSet.get(featValue), labelTestSet.get(featValue)
, names, method)
return decisionTree生成决策树并通过matplotlib可视化
matplotlib相关的函数与上一篇博客中的一样,这里就不再展现了
# 将西瓜数据2.0分割为测试集和训练集
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
# 生成不剪枝的树
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
# 画剪枝前的树
#print("剪枝前的树")
createPlot(xgTreeTrain)
# 画剪枝后的树
#print("剪枝后的树")
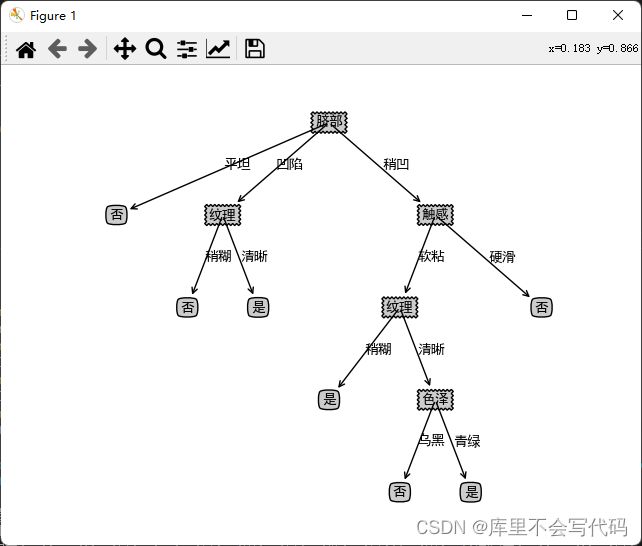
createPlot(xgTreePrePruning)下图为剪枝前的树:
下图为剪枝后的树:
2-2、用自己的数据实现预剪枝
我们还用之前是否申请生源地贷款的数据来做剪枝处理
划分数据、生成树、并可视化:
#将自己的数据分割为测试集和训练集
myDataTrain, myLabelTrain, myDataTest, myLabelTest = splitMyData(myData,myLabel)
# 生成不剪枝的树
myTreeTrain = createTree(myDataTrain, myLabelTrain, myName, method='id3')
# 生成预剪枝的树
myTreePrePruning = createTreePrePruning(myDataTrain, myLabelTrain, myDataTest, myLabelTest, myName, method='id3')
# 画剪枝前的树
#print("剪枝前的树")
createPlot(myTreeTrain)
# 画剪枝后的树
#print("剪枝后的树")
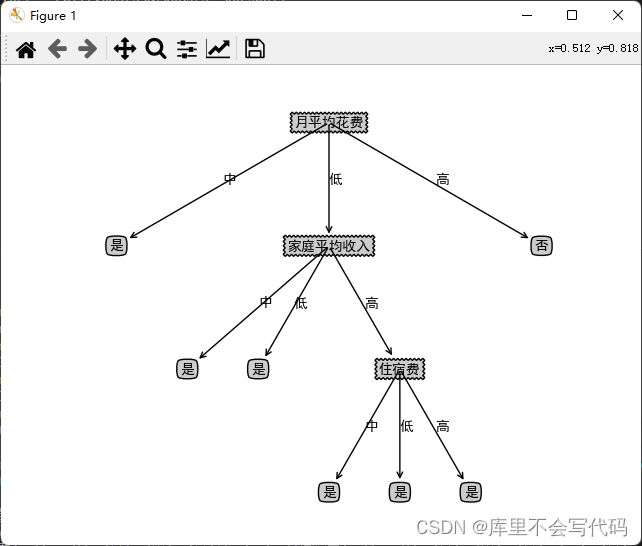
createPlot(myTreePrePruning)剪枝前的树:
剪枝后的树:
三、后剪枝
3-1、西瓜书数据2.0实现后剪枝
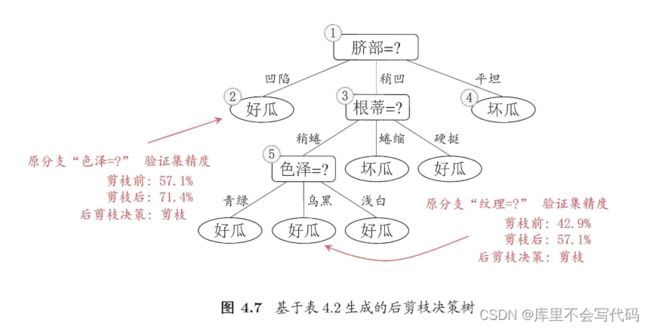
后剪枝就是先构造一颗完整的决策树,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛华性能的提升,则把该子树替换为叶结点。前面已经说过了,使用前面给出的训练集会生成一颗(未剪枝)决策树:
后剪枝首先考虑上图中的结点⑥。若将其领衔的分支剪除,则相当于把⑥替换为叶结点。替换后的叶结点包含编号为{7,15}的训练样本,于是,该叶结点的类别标记为“好瓜”,此时决策树的验证集精度提高至57.1%。于是,后剪枝策略决定剪枝,如下图所示。
下面我们通过python来实现后剪枝
# 创建决策树 带预划分标签
def createTreeWithLabel(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果不划分的标签为
votedLabel = voteLabel(labels)
# 如果结果为单一结果
if len(set(labels)) == 1:
return votedLabel
# 如果没有待分类特征
elif data.size == 0:
return votedLabel
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl
decisionTree = {bestFeatName: {"_vpdl": votedLabel}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
# 将带预划分标签的tree转化为常规的tree
# 函数中进行的copy操作,原因见有道笔记 【YL20190621】关于Python中字典存储修改的思考
def convertTree(labeledTree):
labeledTreeNew = labeledTree.copy()
nodeName = list(labeledTree.keys())[0]
labeledTreeNew[nodeName] = labeledTree[nodeName].copy()
for val in list(labeledTree[nodeName].keys()):
if val == "_vpdl":
labeledTreeNew[nodeName].pop(val)
elif type(labeledTree[nodeName][val]) == dict:
labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val])
return labeledTreeNew
# 后剪枝 训练完成后决策节点进行替换评估 这里可以直接对xgTreeTrain进行操作
def treePostPruning(labeledTree, dataTest, labelTest, names):
newTree = labeledTree.copy()
dataTest = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 取决策节点的名称 即特征的名称
featName = list(labeledTree.keys())[0]
#print("\n当前节点:" + featName)
# 取特征的列
featCol = np.argwhere(names==featName)[0][0]
names = np.delete(names, [featCol])
#print("当前节点划分的数据维度:" + str(names))
#print("当前节点划分的数据:" )
#print(dataTest)
#print(labelTest)
# 该特征下所有值的字典
newTree[featName] = labeledTree[featName].copy()
featValueDict = newTree[featName]
featPreLabel = featValueDict.pop("_vpdl")
#print("当前节点预划分标签:" + featPreLabel)
# 是否为子树的标记
subTreeFlag = 0
# 分割测试数据 如果有数据 则进行测试或递归调用 np的array我不知道怎么判断是否None, 用is None是错的
dataFlag = 1 if sum(dataTest.shape) > 0 else 0
if dataFlag == 1:
# print("当前节点有划分数据!")
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol)
for featValue in featValueDict.keys():
# print("当前节点属性 {0} 的子节点:{1}".format(featValue ,str(featValueDict[featValue])))
if dataFlag == 1 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# 如果是子树则递归
newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names)
# 如果递归后为叶子 则后续进行评估
if type(featValueDict[featValue]) != dict:
subTreeFlag = 0
# 如果没有数据 则转换子树
if dataFlag == 0 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# print("当前节点无划分数据!直接转换树:"+str(featValueDict[featValue]))
newTree[featName][featValue] = convertTree(featValueDict[featValue])
# print("转换结果:" + str(convertTree(featValueDict[featValue])))
# 如果全为叶子节点, 评估需要划分前的标签,这里思考两种方法,
# 一是,不改变原来的训练函数,评估时使用训练数据对划分前的节点标签重新打标
# 二是,改进训练函数,在训练的同时为每个节点增加划分前的标签,这样可以保证评估时只使用测试数据,避免再次使用大量的训练数据
# 这里考虑第二种方法 写新的函数 createTreeWithLabel,当然也可以修改createTree来添加参数实现
if subTreeFlag == 0:
ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size
equalNum = 0
for val in labelTestSet.keys():
equalNum += equalNums(labelTestSet[val], featValueDict[val])
ratioAfterDivision = equalNum / labelTest.size
# print("当前节点预划分标签的准确率:" + str(ratioPreDivision))
# print("当前节点划分后的准确率:" + str(ratioAfterDivision))
# 如果划分后的测试数据准确率低于划分前的,则划分无效,进行剪枝,即使节点等于预划分标签
# 注意这里取的是小于,如果有需要 也可以取 小于等于
if ratioAfterDivision < ratioPreDivision:
newTree = featPreLabel
return newTree生成树并可视化
xgTreeBeforePostPruning = createTreeWithLabel(xgDataTrain, xgLabelTrain, xgName, method='id3')
#print(xgTreeBeforePostPruning)
xgTreePostPruning = treePostPruning(xgTreeBeforePostPruning, xgDataTest, xgLabelTest, xgName)
createPlot(convertTree(xgTreeBeforePostPruning))
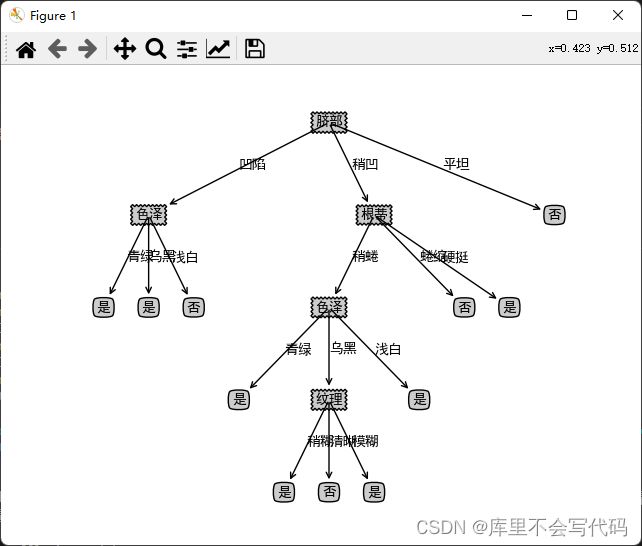
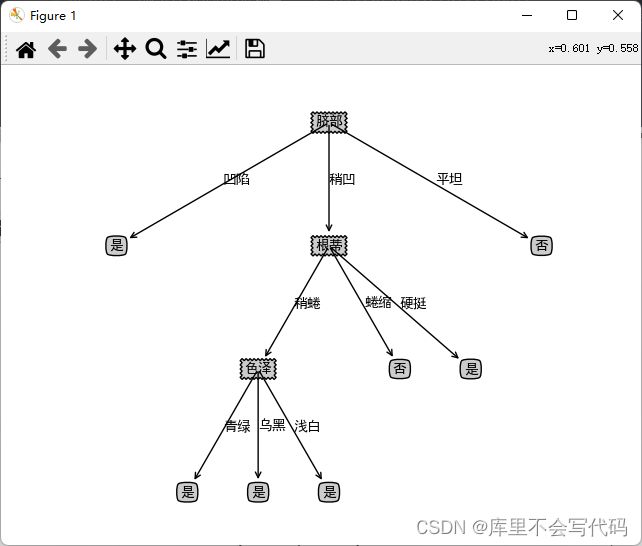
createPlot(xgTreePostPruning)剪枝前的树:
剪枝后的树:
3-2、用自己的数据实现后剪枝
myTreeBeforePostPruning = createTreeWithLabel(myDataTrain, myLabelTrain, myName, method='id3')
#print(myTreeBeforePostPruning)
myTreePostPruning = treePostPruning(myTreeBeforePostPruning, myDataTest, myLabelTest, myName)
createPlot(convertTree(myTreeBeforePostPruning))
createPlot(myTreePostPruning)
剪枝前的树:
剪枝后的树:
四、整体代码
import math #导入一系列数学函数
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
decisionNodeStyle = dict(boxstyle = "sawtooth", fc = "0.8")
leafNodeStyle = dict(boxstyle = "round4", fc = "0.8")
arrowArgs = dict(arrowstyle="<-")
# 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False
#创建数据集
def createDataLH():
data = np.array([['青年','否','否','一般']])
data = np.append(data, [['青年', '否', '否', '好']
,['青年', '是', '否', '好']
, ['青年', '是', '是', '一般']
, ['青年', '否', '否', '一般']
, ['中年', '否', '否', '一般']
, ['中年', '否', '否', '好']
, ['中年', '是', '是', '好']
, ['中年', '否', '是', '非常好']
, ['中年', '否', '是', '非常好']
, ['老年', '否', '是', '非常好']
, ['老年', '否', '是', '好']
, ['老年', '是', '否', '好']
, ['老年', '是', '否', '非常好']
, ['老年', '否', '否', '一般']
], axis = 0)
label = np.array(['否', '否', '是', '是', '否', '否', '否', '是', '是', '是', '是', '是', '是', '是', '否'])
name = np.array(['年龄', '有工作', '有房子', '信贷情况'])
return data,label,name
def createDataXG20():
data = np.array([['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
, ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
, ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
, ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
, ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘']
, ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑']
, ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑']
, ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘']
, ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑']
, ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘']
, ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑']
, ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑']
, ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
, ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑']
, ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑']])
label = np.array(['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否'])
name = np.array(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'])
return data,label,name
def createDataMine():
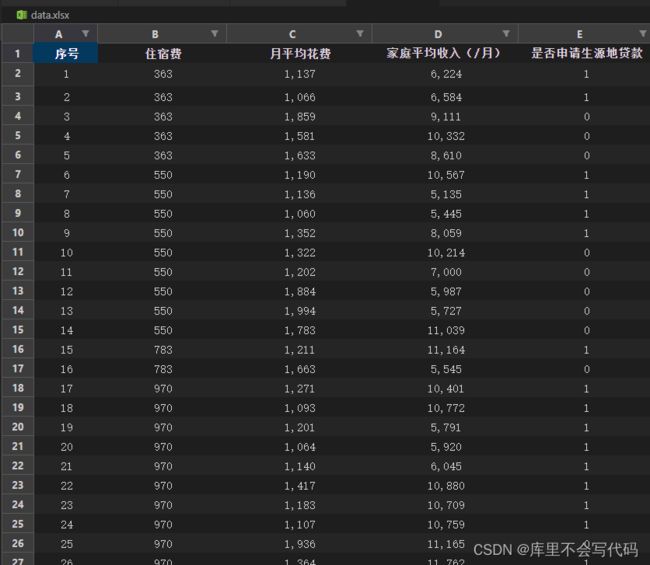
raw_data = pd.read_excel(r'data.xlsx',header=0)
data = raw_data.values[:,1:5]
#使用pandas.cut实现对数据的离散化
data[:,0] = pd.cut(data[:,0],[0,300,800,1200,1400],labels=False)
data[:,1] = pd.cut(data[:,1],[0,1000,1300,1600,2000],labels=False)
data[:,2] = pd.cut(data[:,2],[0,5000,8000,10000,12000],labels=False)
myData = data[:,0:3]
myLabel = data[:,-1]
myData = myData.astype(str)
myLabel = myLabel.astype(str)
#print(myData.dtype)
#print(myLabel.dtype)
myName = ["住宿费","月平均花费","家庭平均收入"]
for i in range(myData.shape[0]):
for j in range(myData.shape[1]):
if(myData[i][j]=='1'):
myData[i][j]='低'
if(myData[i][j]=='2'):
myData[i][j]='中'
if(myData[i][j]=='3'):
myData[i][j]='高'
for k in range(len(myLabel)):
if(myLabel[k]=='0'):
myLabel[k]='否'
if(myLabel[k]=='1'):
myLabel[k]='是'
#print(myData)
#print(myLabel)
return myData,myLabel,myName
def splitXgData20(xgData, xgLabel):
xgDataTrain = xgData[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16],:]
xgDataTest = xgData[[3, 4, 7, 8, 10, 11, 12],:]
xgLabelTrain = xgLabel[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16]]
xgLabelTest = xgLabel[[3, 4, 7, 8, 10, 11, 12]]
return xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest
def splitMyData(myData,myLabel):
myDataTest = np.empty((0,3),dtype=int)
myLabelTest = np.empty((0),dtype=int)
index = 4
#print(myData.shape)
for i in range(int(myData.shape[0]*0.3)):
#print(index)
#print(myData[index,:])
myDataTest = np.append(myDataTest,[myData[index,:]],axis=0)
myData = np.delete(myData,index,axis=0)
myLabelTest = np.append(myLabelTest,myLabel[index])
myLabel = np.delete(myLabel,[index])
index += 2
#print(myData.shape[0])
#print(myDataTest)
#print(myLabelTest)
return myData,myLabel,myDataTest,myLabelTest
# 定义一个常用函数 用来求numpy array中数值等于某值的元素数量
equalNums = lambda x,y: 0 if x is None else x[x==y].size
# 定义计算信息熵的函数
def singleEntropy(x):
"""计算一个输入序列的信息熵"""
# 转换为 numpy 矩阵
x = np.asarray(x)
# 取所有不同值
xValues = set(x)
# 计算熵值
entropy = 0
for xValue in xValues:
p = equalNums(x, xValue) / x.size
entropy -= p * math.log(p, 2)
return entropy
# 定义计算条件信息熵的函数
def conditionnalEntropy(feature, y):
"""计算 某特征feature 条件下y的信息熵"""
# 转换为numpy
feature = np.asarray(feature)
y = np.asarray(y)
# 取特征的不同值
featureValues = set(feature)
# 计算熵值
entropy = 0
for feat in featureValues:
# 解释:feature == feat 是得到取feature中所有元素值等于feat的元素的索引(类似这样理解)
# y[feature == feat] 是取y中 feature元素值等于feat的元素索引的 y的元素的子集
p = equalNums(feature, feat) / feature.size
entropy += p * singleEntropy(y[feature == feat])
return entropy
# 定义信息增益
def infoGain(feature, y):
return singleEntropy(y) - conditionnalEntropy(feature, y)
# 定义信息增益率
def infoGainRatio(feature, y):
return 0 if singleEntropy(feature) == 0 else infoGain(feature, y) / singleEntropy(feature)
'''
# 使用李航数据测试函数 p62
lhData, lhLabel, lhName = createDataLH()
print("书中H(D)为0.971,函数结果:" + str(round(singleEntropy(lhLabel), 3)))
print("书中g(D, A1)为0.083,函数结果:" + str(round(infoGain(lhData[:,0] ,lhLabel), 3)))
print("书中g(D, A2)为0.324,函数结果:" + str(round(infoGain(lhData[:,1] ,lhLabel), 3)))
print("书中g(D, A3)为0.420,函数结果:" + str(round(infoGain(lhData[:,2] ,lhLabel), 3)))
print("书中g(D, A4)为0.363,函数结果:" + str(round(infoGain(lhData[:,3] ,lhLabel), 3)))
# 测试正常,与书中结果一致
# 使用西瓜数据测试函数 p75-p77
xgData, xgLabel, xgName = createDataXG20()
print("书中Ent(D)为0.998,函数结果:" + str(round(singleEntropy(xgLabel), 4)))
print("书中Gain(D, 色泽)为0.109,函数结果:" + str(round(infoGain(xgData[:,0] ,xgLabel), 4)))
print("书中Gain(D, 根蒂)为0.143,函数结果:" + str(round(infoGain(xgData[:,1] ,xgLabel), 4)))
print("书中Gain(D, 敲声)为0.141,函数结果:" + str(round(infoGain(xgData[:,2] ,xgLabel), 4)))
print("书中Gain(D, 纹理)为0.381,函数结果:" + str(round(infoGain(xgData[:,3] ,xgLabel), 4)))
print("书中Gain(D, 脐部)为0.289,函数结果:" + str(round(infoGain(xgData[:,4] ,xgLabel), 4)))
print("书中Gain(D, 触感)为0.006,函数结果:" + str(round(infoGain(xgData[:,5] ,xgLabel), 4)))
'''
# 特征选取
def bestFeature(data, labels, method = 'id3'):
assert method in ['id3', 'c45'], "method 须为id3或c45"
data = np.asarray(data)
labels = np.asarray(labels)
# 根据输入的method选取 评估特征的方法:id3 -> 信息增益; c45 -> 信息增益率
def calcEnt(feature, labels):
if method == 'id3':
return infoGain(feature, labels)
elif method == 'c45' :
return infoGainRatio(feature, labels)
# 特征数量 即 data 的列数量
featureNum = data.shape[1]
# 计算最佳特征
bestEnt = 0
bestFeat = -1
for feature in range(featureNum):
ent = calcEnt(data[:, feature], labels)
if ent >= bestEnt:
bestEnt = ent
bestFeat = feature
# print("feature " + str(feature + 1) + " ent: " + str(ent)+ "\t bestEnt: " + str(bestEnt))
return bestFeat, bestEnt
# 根据特征及特征值分割原数据集 删除data中的feature列,并根据feature列中的值分割 data和label
def splitFeatureData(data, labels, feature):
"""feature 为特征列的索引"""
# 取特征列
features = np.asarray(data)[:,feature]
# 数据集中删除特征列
data = np.delete(np.asarray(data), feature, axis = 1)
# 标签
labels = np.asarray(labels)
uniqFeatures = set(features)
dataSet = {}
labelSet = {}
for feat in uniqFeatures:
dataSet[feat] = data[features == feat]
labelSet[feat] = labels[features == feat]
return dataSet, labelSet
# 多数投票
def voteLabel(labels):
uniqLabels = list(set(labels))
labels = np.asarray(labels)
finalLabel = 0
labelNum = []
for label in uniqLabels:
# 统计每个标签值得数量
labelNum.append(equalNums(labels, label))
# 返回数量最大的标签
return uniqLabels[labelNum.index(max(labelNum))]
# 创建决策树
def createTree(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labels)) == 1:
return labels[0]
# 如果没有待分类特征
elif data.size == 0:
return voteLabel(labels)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTree(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
# 树信息统计 叶子节点数量 和 树深度
def getTreeSize(decisionTree):
nodeName = list(decisionTree.keys())[0]
nodeValue = decisionTree[nodeName]
leafNum = 0
treeDepth = 0
leafDepth = 0
for val in nodeValue.keys():
if type(nodeValue[val]) == dict:
leafNum += getTreeSize(nodeValue[val])[0]
leafDepth = 1 + getTreeSize(nodeValue[val])[1]
else :
leafNum += 1
leafDepth = 1
treeDepth = max(treeDepth, leafDepth)
return leafNum, treeDepth
# 使用模型对其他数据分类
def dtClassify(decisionTree, rowData, names):
names = list(names)
# 获取特征
feature = list(decisionTree.keys())[0]
# 决策树对于该特征的值的判断字段
featDict = decisionTree[feature]
# 获取特征的列
feat = names.index(feature)
# 获取数据该特征的值
featVal = rowData[feat]
# 根据特征值查找结果,如果结果是字典说明是子树,调用本函数递归
if featVal in featDict.keys():
if type(featDict[featVal]) == dict:
classLabel = dtClassify(featDict[featVal], rowData, names)
else:
classLabel = featDict[featVal]
return classLabel
#获取叶节点的数目和树的层数
def getNumLeafs(tree):
numLeafs = 0
#获取第一个节点的分类特征
firstFeat = list(tree.keys())[0]
#得到firstFeat特征下的决策树(以字典方式表示)
secondDict = tree[firstFeat]
#遍历firstFeat下的每个节点
for key in secondDict.keys():
#如果节点类型为字典,说明该节点下仍然是一棵树,此时递归调用getNumLeafs
if type(secondDict[key]).__name__== 'dict':
numLeafs += getNumLeafs(secondDict[key])
#否则该节点为叶节点
else:
numLeafs += 1
return numLeafs
#获取决策树深度
def getTreeDepth(tree):
maxDepth = 0
#获取第一个节点分类特征
firstFeat = list(tree.keys())[0]
#得到firstFeat特征下的决策树(以字典方式表示)
secondDict = tree[firstFeat]
#遍历firstFeat下的每个节点,返回子树中的最大深度
for key in secondDict.keys():
#如果节点类型为字典,说明该节点下仍然是一棵树,此时递归调用getTreeDepth,获取该子树深度
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth
#画出决策树
def createPlot(tree):
# 定义一块画布,背景为白色
fig = plt.figure(1, facecolor='white')
# 清空画布
fig.clf()
# 不显示x、y轴刻度
xyticks = dict(xticks=[], yticks=[])
# frameon:是否绘制坐标轴矩形
createPlot.pTree = plt.subplot(111, frameon=False, **xyticks)
# 计算决策树叶子节点个数
plotTree.totalW = float(getNumLeafs(tree))
# 计算决策树深度
plotTree.totalD = float(getTreeDepth(tree))
# 最近绘制的叶子节点的x坐标
plotTree.xOff = -0.5 / plotTree.totalW
# 当前绘制的深度:y坐标
plotTree.yOff = 1.0
# (0.5,1.0)为根节点坐标
plotTree(tree, (0.5, 1.0), '')
plt.show()
# nodeText:要显示的文本;centerPt:文本中心点,即箭头所在的点;parentPt:指向文本的点;nodeType:节点属性
# ha='center',va='center':水平、垂直方向中心对齐;bbox:方框属性
# arrowprops:箭头属性
# xycoords,textcoords选择坐标系;axes fraction-->0,0是轴域左下角,1,1是右上角
def plotNode(nodeText, centerPt, parentPt, nodeType):
createPlot.pTree.annotate(nodeText, xy=parentPt, xycoords="axes fraction",
xytext=centerPt, textcoords='axes fraction',
va='center', ha='center', bbox=nodeType, arrowprops=arrowArgs)
def plotMidText(centerPt, parentPt, midText):
xMid = (parentPt[0] - centerPt[0]) / 2.0 + centerPt[0]
yMid = (parentPt[1] - centerPt[1]) / 2.0 + centerPt[1]
createPlot.pTree.text(xMid, yMid, midText)
def plotTree(tree, parentPt, nodeTxt):
#计算叶子节点个数
numLeafs = getNumLeafs(tree)
#获取第一个节点特征
firstFeat = list(tree.keys())[0]
#计算当前节点的x坐标
centerPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
#绘制当前节点
plotMidText(centerPt,parentPt,nodeTxt)
plotNode(firstFeat,centerPt,parentPt,decisionNodeStyle)
secondDict = tree[firstFeat]
#计算绘制深度
plotTree.yOff -= 1.0/plotTree.totalD
for key in secondDict.keys():
#如果当前节点的子节点不是叶子节点,则递归
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key],centerPt,str(key))
#如果当前节点的子节点是叶子节点,则绘制该叶节点
else:
#plotTree.xOff在绘制叶节点坐标的时候才会发生改变
plotTree.xOff += 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff,plotTree.yOff),centerPt,leafNodeStyle)
plotMidText((plotTree.xOff,plotTree.yOff),centerPt,str(key))
plotTree.yOff += 1.0/plotTree.totalD
# 使用李航数据测试函数 p62
lhData, lhLabel, lhName = createDataLH()
lhTree = createTree(lhData, lhLabel, lhName, method = 'id3')
#print(lhTree)
#createPlot(lhTree)
# 使用西瓜数据测试函数 p75-p77
xgData, xgLabel, xgName = createDataXG20()
xgTree = createTree(xgData, xgLabel, xgName, method = 'id3')
#print(xgTree)
#createPlot(xgTree)
#使用自己的数据集测试函数
myData,myLabel,myName = createDataMine()
myTree = createTree(myData,myLabel,myName,method='id3')
#print(myTree)
#createPlot(myTree)
# 创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):
"""
预剪枝 需要使用测试数据对每次的划分进行评估
策略说明:原本如果某节点划分前后的测试结果没有提升,根据奥卡姆剃刀原则将不进行划分(即执行剪枝),但考虑到这种策略容易造成欠拟合,
且不能排除后续划分有进一步提升的可能,因此,没有提升仍保留划分,即不剪枝
另外:周志华的书上评估的是某一个节点划分前后对该层所有数据综合评估,如评估对脐部 凹陷下色泽是否划分,
书上取的色泽划分前的精度是71.4%(5/7),划分后的精度是57.1%(4/7),都是脐部下三个特征(凹陷,稍凹,平坦)所有的数据的精度,计算也不易
而我觉得实际计算时,只对当前节点下的数据划分前后进行评估即可,如脐部凹陷时有三个测试样本,
三个样本色泽划分前的精度是2/3=66.7%,色泽划分后的精度是1/3=33.3%,因此判断不划分
"""
trainData = np.asarray(dataTrain)
labelTrain = np.asarray(labelTrain)
testData = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labelTrain)) == 1:
return labelTrain[0]
# 如果没有待分类特征
elif trainData.size == 0:
return voteLabel(labelTrain)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据最优特征进行分割
dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)
# 预剪枝评估
# 划分前的分类标签
labelTrainLabelPre = voteLabel(labelTrain)
labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size
# 划分后的精度计算
if dataTest is not None:
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)
# 划分前的测试标签正确比例
labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size
# 划分后 每个特征值的分类标签正确的数量
labelTrainEqNumPost = 0
for val in labelTrainSet.keys():
labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0
# 划分后 正确的比例
labelTestRatioPost = labelTrainEqNumPost / labelTest.size
# 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
if dataTest is None and labelTrainRatioPre == 0.5:
decisionTree = {bestFeatName: {}}
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, None, None, names, method)
elif dataTest is None:
return labelTrainLabelPre
# 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
elif labelTestRatioPost < labelTestRatioPre:
return labelTrainLabelPre
else :
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, dataTestSet.get(featValue), labelTestSet.get(featValue)
, names, method)
return decisionTree
# 创建决策树 带预划分标签
def createTreeWithLabel(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果不划分的标签为
votedLabel = voteLabel(labels)
# 如果结果为单一结果
if len(set(labels)) == 1:
return votedLabel
# 如果没有待分类特征
elif data.size == 0:
return votedLabel
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl
decisionTree = {bestFeatName: {"_vpdl": votedLabel}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
# 将带预划分标签的tree转化为常规的tree
# 函数中进行的copy操作,原因见有道笔记 【YL20190621】关于Python中字典存储修改的思考
def convertTree(labeledTree):
labeledTreeNew = labeledTree.copy()
nodeName = list(labeledTree.keys())[0]
labeledTreeNew[nodeName] = labeledTree[nodeName].copy()
for val in list(labeledTree[nodeName].keys()):
if val == "_vpdl":
labeledTreeNew[nodeName].pop(val)
elif type(labeledTree[nodeName][val]) == dict:
labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val])
return labeledTreeNew
# 后剪枝 训练完成后决策节点进行替换评估 这里可以直接对xgTreeTrain进行操作
def treePostPruning(labeledTree, dataTest, labelTest, names):
newTree = labeledTree.copy()
dataTest = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 取决策节点的名称 即特征的名称
featName = list(labeledTree.keys())[0]
#print("\n当前节点:" + featName)
# 取特征的列
featCol = np.argwhere(names==featName)[0][0]
names = np.delete(names, [featCol])
#print("当前节点划分的数据维度:" + str(names))
#print("当前节点划分的数据:" )
#print(dataTest)
#print(labelTest)
# 该特征下所有值的字典
newTree[featName] = labeledTree[featName].copy()
featValueDict = newTree[featName]
featPreLabel = featValueDict.pop("_vpdl")
#print("当前节点预划分标签:" + featPreLabel)
# 是否为子树的标记
subTreeFlag = 0
# 分割测试数据 如果有数据 则进行测试或递归调用 np的array我不知道怎么判断是否None, 用is None是错的
dataFlag = 1 if sum(dataTest.shape) > 0 else 0
if dataFlag == 1:
# print("当前节点有划分数据!")
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol)
for featValue in featValueDict.keys():
# print("当前节点属性 {0} 的子节点:{1}".format(featValue ,str(featValueDict[featValue])))
if dataFlag == 1 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# 如果是子树则递归
newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names)
# 如果递归后为叶子 则后续进行评估
if type(featValueDict[featValue]) != dict:
subTreeFlag = 0
# 如果没有数据 则转换子树
if dataFlag == 0 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# print("当前节点无划分数据!直接转换树:"+str(featValueDict[featValue]))
newTree[featName][featValue] = convertTree(featValueDict[featValue])
# print("转换结果:" + str(convertTree(featValueDict[featValue])))
# 如果全为叶子节点, 评估需要划分前的标签,这里思考两种方法,
# 一是,不改变原来的训练函数,评估时使用训练数据对划分前的节点标签重新打标
# 二是,改进训练函数,在训练的同时为每个节点增加划分前的标签,这样可以保证评估时只使用测试数据,避免再次使用大量的训练数据
# 这里考虑第二种方法 写新的函数 createTreeWithLabel,当然也可以修改createTree来添加参数实现
if subTreeFlag == 0:
ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size
equalNum = 0
for val in labelTestSet.keys():
equalNum += equalNums(labelTestSet[val], featValueDict[val])
ratioAfterDivision = equalNum / labelTest.size
# print("当前节点预划分标签的准确率:" + str(ratioPreDivision))
# print("当前节点划分后的准确率:" + str(ratioAfterDivision))
# 如果划分后的测试数据准确率低于划分前的,则划分无效,进行剪枝,即使节点等于预划分标签
# 注意这里取的是小于,如果有需要 也可以取 小于等于
if ratioAfterDivision < ratioPreDivision:
newTree = featPreLabel
return newTree
# 将西瓜数据2.0分割为测试集和训练集
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
# 生成不剪枝的树
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
# 画剪枝前的树
#print("剪枝前的树")
#createPlot(xgTreeTrain)
# 画剪枝后的树
#print("剪枝后的树")
#createPlot(xgTreePrePruning)
#将自己的数据分割为测试集和训练集
myDataTrain, myLabelTrain, myDataTest, myLabelTest = splitMyData(myData,myLabel)
# 生成不剪枝的树
myTreeTrain = createTree(myDataTrain, myLabelTrain, myName, method='id3')
# 生成预剪枝的树
myTreePrePruning = createTreePrePruning(myDataTrain, myLabelTrain, myDataTest, myLabelTest, myName, method='id3')
# 画剪枝前的树
#print("剪枝前的树")
#createPlot(myTreeTrain)
# 画剪枝后的树
#print("剪枝后的树")
#createPlot(myTreePrePruning)
# 书中的树结构 p81 p83
xgTreeBeforePostPruning = {"脐部": {"_vpdl": "是"
, '凹陷': {'色泽':{"_vpdl": "是", '青绿': '是', '乌黑': '是', '浅白': '否'}}
, '稍凹': {'根蒂':{"_vpdl": "是"
, '稍蜷': {'色泽': {"_vpdl": "是"
, '青绿': '是'
, '乌黑': {'纹理': {"_vpdl": "是"
, '稍糊': '是', '清晰': '否', '模糊': '是'}}
, '浅白': '是'}}
, '蜷缩': '否'
, '硬挺': '是'}}
, '平坦': '否'}}
#xgTreeBeforePostPruning = createTreeWithLabel(xgDataTrain, xgLabelTrain, xgName, method='id3')
#print(xgTreeBeforePostPruning)
xgTreePostPruning = treePostPruning(xgTreeBeforePostPruning, xgDataTest, xgLabelTest, xgName)
createPlot(convertTree(xgTreeBeforePostPruning))
createPlot(xgTreePostPruning)
myTreeBeforePostPruning = createTreeWithLabel(myDataTrain, myLabelTrain, myName, method='id3')
#print(myTreeBeforePostPruning)
myTreePostPruning = treePostPruning(myTreeBeforePostPruning, myDataTest, myLabelTest, myName)
createPlot(convertTree(myTreeBeforePostPruning))
createPlot(myTreePostPruning)
五、总结
后剪枝决策树通常比预剪枝决策树保留更多的分支,一般情形下,后剪枝决策树的欠拟合风险小,泛化能力往往优于预剪枝。但后剪枝决策树训练开销比预剪枝大得多。