表格识别之图像基础+轮廓提取+透视校正

一、图片读取cv2.imread（路径，格式3选1）

格式=1：彩色；0：灰度；-1同1，数据结构如下：

前面是彩色图，三维；后面是灰度图，二维。

 二、图像二值化cv2.threshold，cv2.adaptiveThreshold

1. cv2.threshold(对象，阈值，设定值，阈值规则5选1），可处理彩色图。比如：

ret,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)。

ret：True或False，代表有没有读到图片；dst： 目标图像；

表示大于127值的全置为255，否则置为0。

2. cv2.adaptiveThreshold(加工对象，设定值，计算方法2选1，阈值规则5选1，阈值区域大小，常量），只能处理灰色图。比如：

th3 = cv2.adaptiveThreshold(~img,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY,35,-5)，35*35区域？加权平均加上5设为阈值（常量可以为负），大于阈值置为255，否则置0。文字表格效果不错，见下图：

不加“~”，即在源对象前不加“~”，cv2.adaptiveThreshold(img,255,...，效果如下：

三、图像平滑处理（滤波降噪）cv2.blur、cv2.boxFilter、cv2.medianBlur、cv2.GaussianBlur、cv2.bilateralFilter

1. 均值滤波：cv2.blur(对象，核大小)，如：blur = cv2.blur(img,(3,3))，该点对应核中中心，设定值为核大小范围内的所有值平均，边缘处理不详，如下：

2.方框滤波：类似均值滤波，最后一个参数Ture时取均值，为False时，取和。

3.中值滤波：cv2.medianBlur(对象，n),n为大于1的奇数。取中位数，边缘处理不详，如下：

 

4.高斯滤波(貌似用的很多)：cv2.GaussianBlur(对象,核,0,0),核中心权重最大，周围依次下降，后面两个参数，可只设置一个，应该是X、Y轴的计算微调，网上说是标准差之类。

3X1的核，权重为25%、50%、25%。3X3核依次为：0.0625、​0.125、​0.0625、0.125、​0.25、​0.125、0.0625​、0.125、​0.0625。如果将差参数置1，会产生小量变化。

5.双边滤波：cv2.bilateralFilter（对象，n,0,0)，n代表核大小，又有说直径范围，后两个参数分别代表颜色、位置的微调值（标准差）。计算方法不详，同时考虑距离和差值，过于复杂，反应慢。能很好的保留边缘信息。用法举例:cv2.bilateralFilter(gray,9,75,75)。

 6.网上小结： 

• 在不知道用什么滤波器好的时候，优先高斯滤波cv2.GaussianBlur()，然后均值滤波cv2.blur()。
• 斑点和椒盐噪声优先使用中值滤波cv2.medianBlur()。
• 要去除噪点的同时尽可能保留更多的边缘信息，使用双边滤波cv2.bilateralFilter()。
• 线性滤波方式：均值滤波、方框滤波、高斯滤波（速度相对快）。
• 非线性滤波方式：中值滤波、双边滤波（速度相对慢）。

四、图像边缘检测cv2.canny、cv2.sobel、cv2.Laplacian

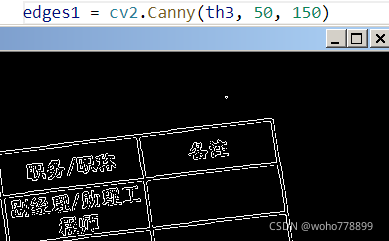
1、cv2.Canny(对象，最小值，最大值），可选参数apertureSize=7，最大为7效果不错，线框闭合，对比如下：

apertureSize： aperture size for the Sobel operator.算子的孔径大小。 

 2、cv2.Sobel(对象，深度，X,Y)

 

 3、拉普拉斯cv2.laplacian(对象，深度），可选核大小。 

 五、内核设置：ker=cv2.getStructuringElement( 形状3选1，大小，中心) ,返回指定的结构元素，即规则。

形状为下面三种，中心设置好象只对交叉形有效。

矩形：MORPH_RECT;

交叉形：MORPH_CROSS;用第三个参加调整中心点（见下图）

椭圆形：MORPH_ELLIPSE;

六、 腐蚀:cv2.erode(对象，规则)方法用于对图像进行腐蚀。

 通常在二进制图像上执行。dst = cv.erode(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]])。比如：cv2.erode(bin_src,kernel,iterations = 1)

它至少需要两个输入，一个是我们的原始图像，第二个是决定操作性质的结构元素或内核。仅当满足内核条件要求下所有像素均为1时，原始图像中的像素被视为1，否则设为零，相当于“求和”操作。效果是黑色背景变大。

设置线性核，可取出表格线：kernel = cv2.getStructuringElement(cv2.MORPH_RECT,(33,1))

效果如下：

图中上半截为二进制表格图像，下半截为经过33*1线性核腐蚀后的效果，取出了表格横线。

七、膨胀 ：cv2.dilate(对象，规则)：与腐蚀相反的效果。

dst = cv2.dilate(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]])

原理解析：比如：设置7*1线性核>>> kernel = cv2.getStructuringElement(cv2.MORPH_RECT,(7,1))>>> dilatedcol = cv2.dilate(binary,kernel,iterations = 1)，前后对比如下：

 以长度7为核进行膨胀，即以本身点为中点，前后各3个点，如有1个为1即计为1，全0才记为0，相当于“求或”操作。

将前景物体变大，理解成白色部分变粗加长（在图片上画上黑色背景变小,迭代次数增加，白色断线逐渐相连。）

八、直线检测 cv2.HoughLinesP(对象,1,np.pi/180,n)，可选minLineLength=30,maxLineGap=5。

 cv2.HoughLinesP(edges,1,np.pi/360,10,minLineLength=30,maxLineGap=5)

可选项maxLineGap=5，表示线段断点距离，不能直接用数字，前面的英文不能省。该值越大，线段越长越多，见下图：

 必选项第4项threshold参数，数值，表示检测一条直线所需最少的曲线交点，值越小线段越多。

返回结果为两个坐标点的数组，如下：

 九、轮廓检测cv2.findContours()、回画cv2.drawContours()、最小外接矩形cv2.minAreaRect()、外接多边形cv2.approxPolyDP

1、cv2.findContours(二值对象，模式4选1，方法多选1)，比如：

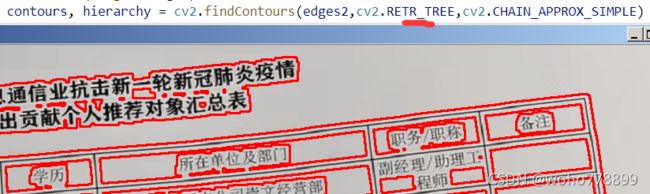
contours, hierarchy = cv2.findContours(binary,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) 

第二个参数，其中EXTERNAL表示只检测外轮廓，但一定是封闭的，TREE表示树型，大轮廓中的小轮廓也检测出来，对比如下： 

 

 

 返回的第一个值，为列表类型，长短不一，如下：

返回的第二个值，表示各个轮廓序列和层级等关系，没感觉到实用性，数据形式如下：

2、在图像上绘制轮廓cv2.drawContours(图像，轮廓，第几条，颜色，线宽等），比如：

 提取最长轮廓，单独显示：

提取面积最大的轮廓cv2.contourArea(contour)，对于复杂的表格场景，这个似乎比提取最长轮廓更准备识别出表格：

longest=largest=np.array([[[ 1, 1]],[[ 1, 2]]], dtype=np.int32)
for ct in contours:
    if len(ct)>=len(longest):
        longest=ct
    if cv2.contourArea(ct)>cv2.contourArea(largest):
        largest=ct
cv2.drawContours(img,longest,-1,(0,0,255),5) 
cv2.drawContours(img,largest,-1,(0,255,0),2) 
print('共找到',len(contours),'个轮廓，最长轮廓长为',len(longest),'轮廓面积为：',cv2.contourArea(longest))
print('面积最大轮廓长为',len(largest),'轮廓面积为：',cv2.contourArea(largest))

效果如下，其中绿色框为最大面积轮廓提取法，红色为最长轮廓数提取法：

  3、最小矩形 cv2.minAreaRect(轮廓)，如下：

 

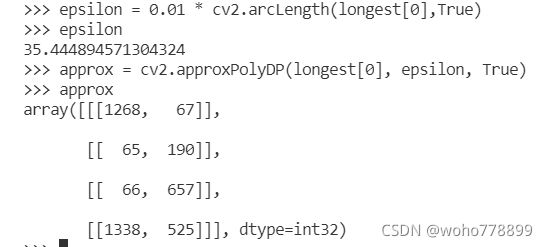
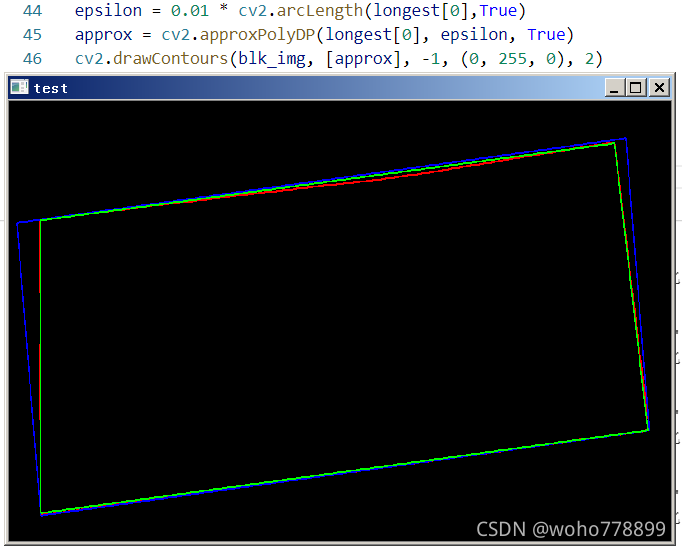
4、外接多边形cv2.approxPolyDP(轮廓，距离，是否闭合)，距离double epsilon：判断点到相对应的line segment 的距离的阈值。（距离大于此阈值则舍弃，小于此阈值则保留，epsilon越小，折线的形状越“接近”曲线。）是否闭合bool closed：曲线是否闭合的标志位。返回坐标点。

arcLength函数，主要是计算图像轮廓的周长，第二个参数表示是否闭合，返回double数。如下：

 效果如下：

 可以看出，多边形对比于外接最小矩形，更接近真实情况，返回坐标值，可直接校正操作。

 如果所得多边形，多于4个点，可借助矩形点求最近值来确定4个点。不能通过调整epsilon参数循环获得准确坐标，如下：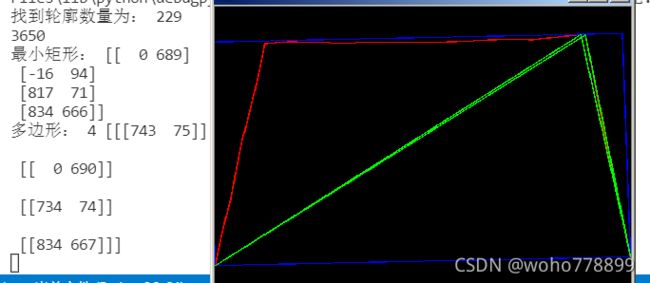

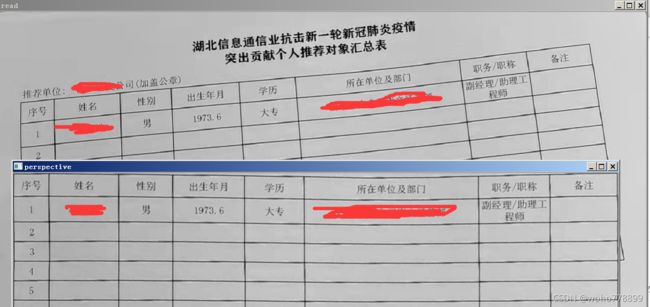
十、图像透视校正：cv2.getPerspectiveTransform

1、多边形顶点数组降维确定，approx.sum(axis=维度），维度取值为：0、1、2等。

顶点数据结构如下：

 可看出这是一个4*1*2结构的数据，直接用approx.sum(axis=1)消除第二维，就可以得到一个4*2的四个顶点坐标数据，当然也可写个循环取出来，结果如下：

关于这个axis参数，=0消除第一维，其他维数求和，=1消除第二维，其他求和，依次类推。如下：

2.四边形4点顺序确定。通过np.argsort(four_d,axis=0)分组实现

关于确定左上角点P1，网上用np.argmin(approx),这个不能达到目的，不能以简单的最小值、最大值来确定左上、右下的角点坐标，如下：

 这个argmin函数返回的是：所有数据混合后最小值的索引，如果加上参数axis=0或1（理解为行或列），则返回每列或每行（顺序颠倒）的最小值数组。如4*2，=0时，返回二个值数组，见下图：

显然，理论依据不成立。

可采取二分法来找出顶点坐标。

#四点排序：左上、右上、右下、左下#画水平横线，将四点分上下两部分，即根据Y值分成1、2一组，3、4一组，再分组比较X值
four_d=approx.sum(axis=1)#降维，生成四点的坐标
s_four_d=four_d.copy()
s=np.argsort(four_d,axis=0)#按列排序，返回每列索引值
if four_d[s[0][1]][0]

运行结果如下：

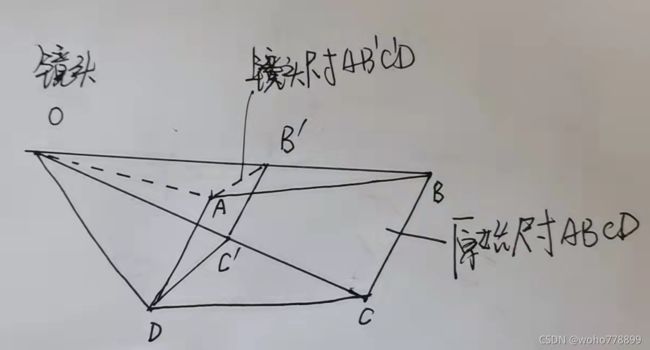
3.原始尺寸的还原。如图：

 网上的各取XY两个方向的最大值，显然有误差，因为C'D

#还原图像尺寸
(tl, tr, br, bl) = s_four_d
# 计算轮廓的宽和长，分别大小
widthA = np.sqrt(((tl[0]-tr[0])**2) + ((tl[1]-tr[1])**2))
widthB = np.sqrt(((bl[0]-br[0])**2) + ((bl[1] - br[1])**2))
widthMax = max(int(widthB), int(widthA))
widthMin = min(int(widthB), int(widthA))
heightA = np.sqrt(((tl[0]-bl[0])**2) + ((tl[1]-bl[1])**2))
heightB = np.sqrt(((tr[0]-br[0])**2) + ((tr[1] - br[1])**2))
heightMax = max(int(heightA), int(heightB))
heightMin = min(int(heightA), int(heightB))
#判断XY两个方向失真比率
if widthMax/widthMin>heightMax/heightMin:#如果y方向失真严重些，即两横线比率大于两竖线比率。
    img_width=widthMax#以X长边（横线）为基准
    img_height=int(((widthMax/widthMin-heightMax/heightMin)/2+1)*heightMax) #校正Y方向增量，两比率差值除以2
else:#否则，如果X方向失真大些
    img_height=heightMax#以Y（竖线）长边为基准
    img_width=int(((heightMax/heightMin-widthMax/widthMin)/2+1)*widthMax)#校正X方向增量
# 四个角的位置信息
transform_axis = np.array([
    [0, 0],
    [img_width-1, 0],
    [img_width-1, img_height-1],
    [0, img_height-1],
], dtype='float32')

4、建立透视规则：tf=cv2.getPerspectiveTransform(源4点，新4点),点的类型为浮点型，如不是，可通过s_four_d=s_four_d.astype(np.float32)转成浮点32型。返回规则，生成新图像时需要用上，实为3*3矩阵，如下：

>>> m=cv2.getPerspectiveTransform(s_four_d,transform_axis)
>>> m
array([[ 1.08313688e+00, -2.31935092e-03, -6.99632205e+01],
       [ 1.13144710e-01,  1.10661046e+00, -2.17610393e+02],
       [ 9.56494920e-06,  1.26357675e-04,  1.00000000e+00]])

5、生成透视后的图像：cv2.warpPerspective(原图像，规则，新图像大小），返回新图像，比如：

img_out = cv2.warpPerspective(img, m, (img_width, img_height))，效果如下：

6、透视图像的边缘处理。表格线太靠近边缘，可各增加5个点。表头没有透视进来，可设置一个Y方向的增量，将表头也透视进来，部分代码如下：

d_y=100#四点外的图像同步透视，设置Y方向的增量，比如表头
transform_axis = np.array([
    [5, 5+d_y],
    [img_width+4, 5+d_y],
    [img_width+4, img_height+4+d_y],
    [5, img_height+4+d_y],
], dtype='float32')
#图像透视校正：cv2.getPerspectiveTransform(源4点，新4点)，浮点型,返回规则矩阵
m=cv2.getPerspectiveTransform(s_four_d,transform_axis)
#使用cv2.warpPerspective()和矩阵规则，获得变化后的图像
img_out = cv2.warpPerspective(img, m, (img_width+10, img_height+10+d_y))

效果如下：

 透视不足的地方，用黑边进行了代替，还行。

十一、零点距离图：cv2.distanceTransform（对象，距离类型，掩模）

用法：dist = cv2.distanceTransform(gray, cv2.DIST_L1, cv2.DIST_MASK_PRECISE)，操作对象为二值图片，灰色图也可以。距离类型有多种，其中cv2.DIST_L1为基本型，|X1-X2|+|Y1-Y2|,数步值，即X、Y两个方向步数之和；cv2.DIST_L2为欧氏距离，两点的直线距离，平方和再开方。得到距离图为浮点32型，如下：

 显示效果时需要将值作个除法：cv2.imshow("distance", dist/155)，如右图：

 具体运用时，可遍历所有点，只保留最大值dist.max(),或接近最大值的范围值，如>dist.max()*0.8，这样可以更好的保留骨干信息。