神经网络与深度学习6---网络优化与正则化
网络优化与正则化
- 为什么神经网络可以拟合任何函数
- 激活函数的选择
- 参数初始化
-
- 为什么不能将参数初始化为全零
- 参数初始化的目的
- 基于方差缩放的参数初始化
- 正交初始化
- 理解Dropout
-
- Dropout起作用的原因
- Dropout的使用限制
- 归一化
-
- Batch Normalization
- Layer Normalization
本文是邱锡鹏教授撰写的《神经网络与深度学习》一书中 第7章:网络优化与正则化 的读书笔记,主要内容是一些本人觉得比较值得记录的内容,中间也会包括一些拓展和思考。
为什么神经网络可以拟合任何函数
从黎曼和定积分的角度考虑,对任意一个连续函数,它都可以由若干个阶梯函数求和表示:

因此我们只要证明神经元可以拟合任意阶梯函数,那么就可以间接“证明” 这个神经网络可以拟合任何连续函数。
假设神经网络的激活函数是sigmoid函数 1 1 + e ( w T x + b ) \frac{1}{1+e^{(w^Tx +b)}} 1+e(wTx+b)1,改变 w w w 和 b b b,sigmoid图形有以下变化:

- 通过改变偏置 b b b,可以控制曲线的位置
- 通过改变权重 w w w,可以控制曲线的陡度;当 w w w 取到一个很大的值时,s形曲线非常接近与一个阶跃函数
那么对于两个神经元,我们可以通过控制 w w w 和 b b b,获得 任意阶梯函数的近似函数:
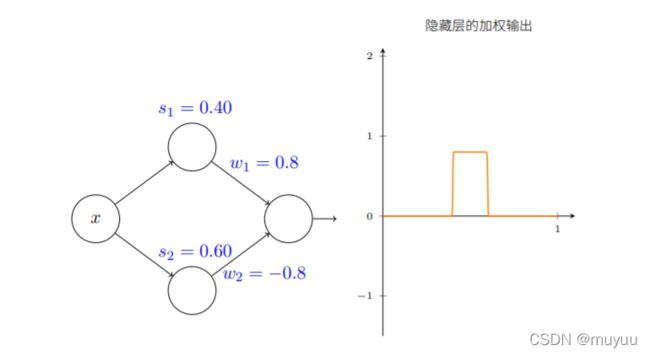
例如,对于函数 f ( x ) = 0.2 + 0.4 x 2 + 0.3 x ∗ sin ( 15 x ) + 0.05 cos ( 50 x ) f(x) = 0.2 + 0.4x^2 + 0.3x * \text{sin}(15x) + 0.05 \text{cos}(50x) f(x)=0.2+0.4x2+0.3x∗sin(15x)+0.05cos(50x),它的图形如下图右边的曲线所示。而我们用 10 个神经元就可以粗略的拟合出它的走势,事实上,只要神经元数量足够多,我们就可以以任意精度来拟合原函数 f ( x ) f(x) f(x)

总结来说,一个前馈神经网络如果具有线性输出层和至少一层具有任何一种‘‘挤压’’性质的激活函数的隐藏层,只要给予网络足够数量的隐藏单元,它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的Borel 可测函数。
上面所谓的‘‘挤压’’ 性质,即 激活函数可以通过线性组合近似任意阶梯函数,例如上面我们论证了两个sigmoid函数的线性组合可以近似任意阶梯函数,而常用的 Relu函数需要三个函数的线性组合即可近似任意阶梯函数。
##########################################################################
激活函数的选择
从上一节的解释我们知道,只要是具有‘‘挤压’’性质的函数,理论上都可以作为激活函数。而在实际使用中,选择激活函数的另一个重要考量是激活函数导数的性质,例如是否可导,导数值是否在合理范围内(涉及到梯度爆炸以及梯度消失),以及求导复杂度等等。
- sigmoid函数
sigmoid ( x ) = 1 1 + e − x \text{sigmoid}(x) = \frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
它的函数图像是:

sigmoid函数将输入压缩到区间 (0,1) 上,且在零点附近接近线性函数。其导数为:
d d x sigmoid ( x ) = e − x ( 1 + e − x ) 2 = sigmoid ( x ) ( 1 − sigmoid ( x ) ) \frac{d}{dx}\text{sigmoid}(x) = \frac{e^{-x}}{(1+e^{-x})^2} = \text{sigmoid}(x)(1-\text{sigmoid}(x)) dxdsigmoid(x)=(1+e−x)2e−x=sigmoid(x)(1−sigmoid(x))
图像如下:
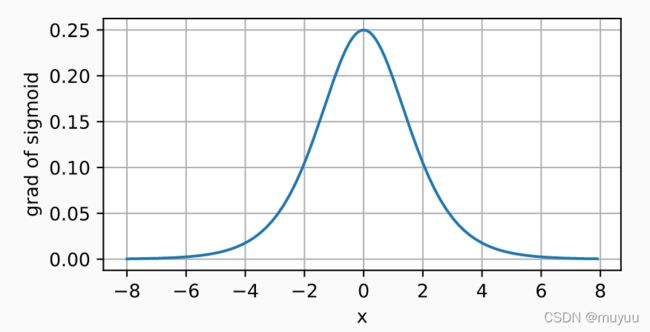
sigmoid函数的导数最大值0.25,在 x = 0 x=0 x=0 时达到,而在两边逐渐趋于零。由于导数最大值也仅为0.25,因此sigmoid函数作为激活函数时,一旦模型深度较大,很容易引起“梯度消失”现象。
- tanh函数
tanh ( x ) = 1 − e − 2 x 1 + e − 2 x \text{tanh}(x) = \frac{1-e^{-2x}}{1+e^{-2x}} tanh(x)=1+e−2x1−e−2x
它将输入压缩到区间 (-1,1) 上,且关于原点中心对称:
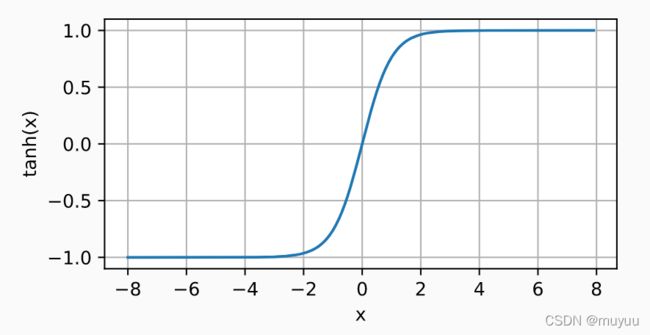
tanh函数的导数是:
d d x tanh ( x ) = 1 − tanh 2 ( x ) \frac{d}{dx}\text{tanh}(x) = 1- \text{tanh}^2(x) dxdtanh(x)=1−tanh2(x)
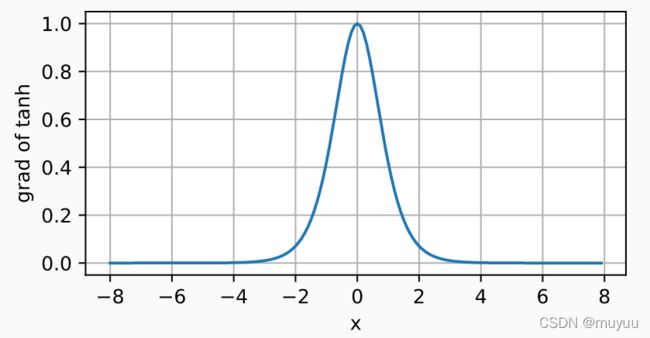
tanh函数的导数在零点处取得最大值1,且越往两边走,导数越趋向于零。由于tanh函数导数最大值可以达到1,如果可以将梯度维持在零点附近,那么可以较好得避免梯度消失以及梯度爆炸的情况。
- ReLu函数
R e L u ( x ) = m a x ( x , 0 ) ReLu(x) = max(x,0) ReLu(x)=max(x,0)
ReLu函数的定义十分简单,求导表现也非常好:要么让参数消失,要么让参数通过。这使得优化表现得更好,并且由于它梯度恒为1或0,因此比起上面两个函数,减轻了梯度消失的问题,并且求导计算量也大大减小。
##########################################################################
参数初始化
为什么不能将参数初始化为全零
以一个三层网络为例:
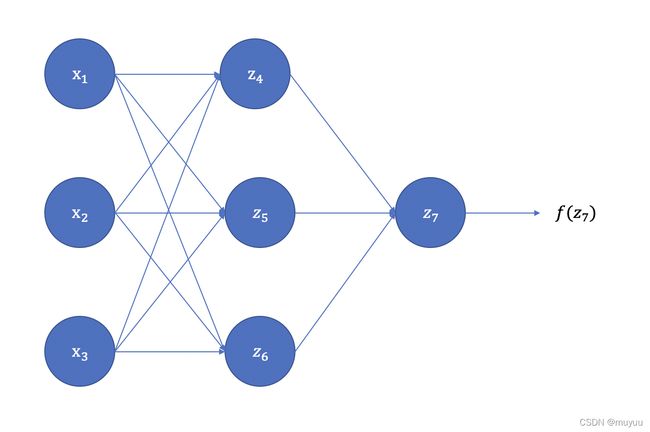
其中 z 4 = w 14 ∗ x 1 + w 24 ∗ x 2 + w 34 ∗ x 3 + b 4 z 5 = w 15 ∗ x 1 + w 25 ∗ x 2 + w 35 ∗ x 3 + b 5 z 6 = w 16 ∗ x 1 + w 26 ∗ x 2 + w 36 ∗ x 3 + b 6 z_4=w_{14}∗x_1+w_{24}∗x_2+w_{34}∗x_3+b_4\\ z_5=w_{15}∗x_1+w_{25}∗x_2+w_{35}∗x_3+b_5\\ z_6=w_{16}∗x_1+w_{26}∗x_2+w_{36}∗x_3+b_6\\ z4=w14∗x1+w24∗x2+w34∗x3+b4z5=w15∗x1+w25∗x2+w35∗x3+b5z6=w16∗x1+w26∗x2+w36∗x3+b6
经过激活函数得到:
a 4 = g ( z 4 ) a 5 = g ( z 5 ) a 6 = g ( z 6 ) a_4 = g(z_4)\\ a_5 = g(z_5)\\ a_6 = g(z_6)\\ a4=g(z4)a5=g(z5)a6=g(z6)
输出层:
z 7 = w 47 a 4 + w 57 a 5 + w 67 a 6 z_7 = w_{47}a_4 + w_{57}a_5 + w_{67}a_6\\ z7=w47a4+w57a5+w67a6
经过输出层激活函数:
a 7 = f ( z 7 ) a_7 = f(z_7) a7=f(z7)
假设真实标签为 y y y,损失函数记为 Loss ( y , a 7 ) \text{Loss}(y,a_7) Loss(y,a7),那么根据链式法则:
∂ Loss ( y , a 7 ) ∂ w 47 = ∂ Loss ( y , a 7 ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ ∂ z 7 ∂ w 47 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ a 4 \begin{aligned} \frac{\partial \text{Loss}(y,a_7)}{\partial w_{47}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial a_7} * \frac{\partial a_7}{\partial z_7} * \frac{\partial z_7}{\partial w_{47}}\\ &= \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * a_4 \end{aligned} ∂w47∂Loss(y,a7)=∂a7∂Loss(y,a7)∗∂z7∂a7∗∂w47∂z7=∂z7∂Loss(y,a7)∗a4
同理可得:
∂ Loss ( y , a 7 ) ∂ w 57 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ a 5 ∂ Loss ( y , a 7 ) ∂ w 67 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ a 6 \begin{aligned} \frac{\partial \text{Loss}(y,a_7)}{\partial w_{57}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * a_5\\ \frac{\partial \text{Loss}(y,a_7)}{\partial w_{67}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * a_6 \end{aligned} ∂w57∂Loss(y,a7)∂w67∂Loss(y,a7)=∂z7∂Loss(y,a7)∗a5=∂z7∂Loss(y,a7)∗a6
而对于第一层的参数 w i 4 , w i 5 , w i 6 , i = { 1 , 2 , 3 } w_{i4},w_{i5},w_{i6},i= \{1,2,3\} wi4,wi5,wi6,i={1,2,3},有:
∂ Loss ( y , a 7 ) ∂ w i 4 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ ∂ z 7 ∂ a 4 ∗ ∂ a 4 ∂ z 4 ∗ x i = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ w 47 ∗ ∂ a 4 ∂ z 4 ∗ x i ∂ Loss ( y , a 7 ) ∂ w i 5 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ ∂ z 7 ∂ a 5 ∗ ∂ a 5 ∂ z 5 ∗ x i = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ w 57 ∗ ∂ a 5 ∂ z 5 ∗ x i ∂ Loss ( y , a 7 ) ∂ w i 6 = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ ∂ z 7 ∂ a 6 ∗ ∂ a 6 ∂ z 6 ∗ x i = ∂ Loss ( y , a 7 ) ∂ z 7 ∗ w 67 ∗ ∂ a 6 ∂ z 6 ∗ x i \begin{aligned} \frac{\partial \text{Loss}(y,a_7)}{\partial w_{i4}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * \frac{\partial z_7}{\partial a_4} * \frac{\partial a_4}{\partial z_4} * x_i = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * w_{47} * \frac{\partial a_4}{\partial z_4} * x_i\\ \frac{\partial \text{Loss}(y,a_7)}{\partial w_{i5}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * \frac{\partial z_7}{\partial a_5} * \frac{\partial a_5}{\partial z_5} * x_i = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * w_{57} * \frac{\partial a_5}{\partial z_5} * x_i\\ \frac{\partial \text{Loss}(y,a_7)}{\partial w_{i6}} & = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * \frac{\partial z_7}{\partial a_6} * \frac{\partial a_6}{\partial z_6} * x_i = \frac{\partial \text{Loss}(y,a_7)}{\partial z_7} * w_{67} * \frac{\partial a_6}{\partial z_6} * x_i\\ \end{aligned} ∂wi4∂Loss(y,a7)∂wi5∂Loss(y,a7)∂wi6∂Loss(y,a7)=∂z7∂Loss(y,a7)∗∂a4∂z7∗∂z4∂a4∗xi=∂z7∂Loss(y,a7)∗w47∗∂z4∂a4∗xi=∂z7∂Loss(y,a7)∗∂a5∂z7∗∂z5∂a5∗xi=∂z7∂Loss(y,a7)∗w57∗∂z5∂a5∗xi=∂z7∂Loss(y,a7)∗∂a6∂z7∗∂z6∂a6∗xi=∂z7∂Loss(y,a7)∗w67∗∂z6∂a6∗xi
如果参数全部初始化为零,并且激活函数是tanh函数,那么:
z 4 = z 5 = z 6 = 0 a 4 = a 5 = a 6 = 0 \begin{aligned} z_4 = z_5 = z_6 = 0\\ a_4 = a_5 = a_6 = 0\\ \end{aligned} z4=z5=z6=0a4=a5=a6=0
因此 w 47 , w 57 , w 67 w_{47},w_{57},w_{67} w47,w57,w67 梯度更新相同,又由于 w 47 , w 57 , w 67 w_{47},w_{57},w_{67} w47,w57,w67的初始值都为零,因此一个batch之后 w 47 = w 57 = w 67 w_{47} = w_{57} = w_{67} w47=w57=w67, 且都得不到更新。
对于 w i 4 , w i 5 , w i 6 , i = { 1 , 2 , 3 } w_{i4},w_{i5},w_{i6},i= \{1,2,3\} wi4,wi5,wi6,i={1,2,3}, 根据前面的推导式,如果 w 47 = w 57 = w 67 w_{47} = w_{57} = w_{67} w47=w57=w67,那么总有:
w 14 = w 24 = w 34 w 15 = w 25 = w 35 w 16 = w 26 = w 36 \begin{aligned} w_{14} = w_{24} = w_{34}\\ w_{15} = w_{25} = w_{35}\\ w_{16} = w_{26} = w_{36}\\ \end{aligned} w14=w24=w34w15=w25=w35w16=w26=w36
这种情况称为 对称权重现象,并且如果参数全部初始化为零, 激活函数是tanh函数,那么这些权重也得不到更新。如果激活函数是sigmoid函数,那么可能可以避免权重完全不更新的情况,但是 对称权重现象 是无法避免的。事实上,根据推导过程,只要权值都初始化为相同的值,就会导致该现象,因此在参数初始化时,也不能将它们初始化成一样的值。
参数初始化的目的
从计算的角度来看,参数初始化的一个首要目的就是要 在训练开始阶段激活尽量多的神经元,或者说让尽量多的神经元得到有意义的更新。在这个思想的指导下,我们首先可以回答一些简单的问题:
-
为什么初始化值不能太大?
对于sigmoid、tanh激活函数,初始化值太大,使得流入激活函数的值过大,造成饱和现象,当反向传播时,会使得梯度极小,导致梯度消失;
而对于Relu激活函数,如果初始化值太大,造成神经元的输出值过大,矩阵乘积发生爆炸,容易造成数值溢出,以及梯度爆炸。 -
为什么初始化值不能太小?
初始化太小时,经过多层网络,输出值变得极小,在反向传播时也会使得梯度极小,导致梯度消失。(ReLU函数也受此影响!) -
为什么初始值不能相同?
根据上一节的内容,初始值相同会导致 对称权重现象 ,造成大量的神经元趋于一致,降低训练效果。
基于方差缩放的参数初始化
一般来说,我们会利用高斯分布,均匀分布等分布来初始化权重(偏置一般可以初始化为零)。在不指定任何先验的情况下,可以将均值设为0,方差 σ 2 \sigma^2 σ2 是一个超参数。下面我们先看,在不做任何处理的情况下,以(均值0,方差 σ 2 \sigma^2 σ2 )来初始化权重会有怎样的效果:
在一个神经网络中,记 a ( l ) a^{(l)} a(l) 为第 l l l 层的一个神经元,那么它的结果由上一层的 M l − 1 M_{l-1} Ml−1 个神经元的输出值 a i ( l − 1 ) , 1 ≤ i ≤ M l − 1 a^{(l-1)}_i, 1\leq i \leq M_{l-1} ai(l−1),1≤i≤Ml−1 决定:
a ( l ) = f ( ∑ i = 1 M l − 1 w i ( l ) a i ( l − 1 ) ) a^{(l)} = f(\sum_{i=1}^{M_{l-1}} w_i^{(l)} a^{(l-1)}_i) a(l)=f(i=1∑Ml−1wi(l)ai(l−1))
其中 f f f 是激活函数。由于大部分激活函数在0附近都是近似线性的,这里简单起见,假设 f ( x ) = x f(x) = x f(x)=x。那么 a ( l ) a^{(l)} a(l) 的均值和方差为(假设 a i ( l − 1 ) a^{(l-1)}_i ai(l−1) 均值为0):
E ( a ( l ) ) = E ( ∑ i = 1 M l − 1 w i ( l ) a i ( l − 1 ) ) = ∑ i = 1 M l − 1 E ( w i ( l ) ) E ( a i ( l − 1 ) ) = 0 E(a^{(l)}) = E(\sum_{i=1}^{M_{l-1}} w_i^{(l)} a^{(l-1)}_i) = \sum_{i=1}^{M_{l-1}} E(w_i^{(l)}) E(a^{(l-1)}_i) = 0 E(a(l))=E(i=1∑Ml−1wi(l)ai(l−1))=i=1∑Ml−1E(wi(l))E(ai(l−1))=0
在计算 a ( l ) a^{(l)} a(l) 的方差前,我们先推导一下 D ( X Y ) D(XY) D(XY) 的公式,这里假设 X , Y X,Y X,Y 相互独立。已知方差推导公式为 D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X) D(X)=E(X2)−E2(X),那么有:
D ( X Y ) = E ( X 2 Y 2 ) − E 2 ( X Y ) = E ( X 2 ) E ( Y 2 ) − E 2 ( X ) E 2 ( Y ) = ( D ( X ) + E 2 ( X ) ) ∗ ( D ( Y ) + E 2 ( Y ) ) − E 2 ( X ) E 2 ( Y ) = D ( X ) D ( Y ) + E 2 ( X ) D ( Y ) + E 2 ( Y ) D ( X ) \begin{aligned} D(XY) &= E(X^2Y^2) - E^2(XY)\\ &= E(X^2)E(Y^2) - E^2(X)E^2(Y)\\ &= (D(X)+E^2(X))*(D(Y)+E^2(Y)) - E^2(X)E^2(Y)\\ &= D(X)D(Y) + E^2(X) D(Y) + E^2(Y) D(X) \end{aligned} D(XY)=E(X2Y2)−E2(XY)=E(X2)E(Y2)−E2(X)E2(Y)=(D(X)+E2(X))∗(D(Y)+E2(Y))−E2(X)E2(Y)=D(X)D(Y)+E2(X)D(Y)+E2(Y)D(X)
那么 a ( l ) a^{(l)} a(l) 的方差为:
D ( a ( l ) ) = ∑ i = 1 M l − 1 D ( w i ( l ) ) D ( a i ( l − 1 ) ) + E 2 ( w i ( l ) ) D ( a i ( l − 1 ) ) + E 2 ( a i ( l − 1 ) ) D ( w i ( l ) ) = ∑ i = 1 M l − 1 D ( w i ( l ) ) D ( a i ( l − 1 ) ) + 0 ∗ D ( a i ( l − 1 ) ) + 0 ∗ D ( w i ( l ) ) = ∑ i = 1 M l − 1 D ( w i ( l ) ) D ( a i ( l − 1 ) ) = M l − 1 D ( w i ( l ) ) D ( a ( l − 1 ) ) = ∏ l = 1 l M l − 1 D ( w i ( l ) ) D ( a ( 0 ) ) \begin{aligned} D(a^{(l)}) &= \sum_{i=1}^{M_{l-1}} D(w_i^{(l)})D(a^{(l-1)}_i) + E^2(w_i^{(l)}) D(a^{(l-1)}_i) + E^2(a^{(l-1)}_i) D(w_i^{(l)}) \\ &= \sum_{i=1}^{M_{l-1}} D(w_i^{(l)})D(a^{(l-1)}_i) + 0*D(a^{(l-1)}_i) + 0*D(w_i^{(l)}) \\ &= \sum_{i=1}^{M_{l-1}} D(w_i^{(l)})D(a^{(l-1)}_i)\\ &= M_{l-1}D(w_i^{(l)})D(a^{(l-1)})\\ & = \prod_{l=1}^{l} M_{l-1}D(w_i^{(l)})D(a^{(0)}) \end{aligned} D(a(l))=i=1∑Ml−1D(wi(l))D(ai(l−1))+E2(wi(l))D(ai(l−1))+E2(ai(l−1))D(wi(l))=i=1∑Ml−1D(wi(l))D(ai(l−1))+0∗D(ai(l−1))+0∗D(wi(l))=i=1∑Ml−1D(wi(l))D(ai(l−1))=Ml−1D(wi(l))D(a(l−1))=l=1∏lMl−1D(wi(l))D(a(0))
也就是说 随着层数加深,神经元输出值的均值保持为0,而方差确不断放大或者缩小 M l − 1 D ( w i ( l ) ) M_{l-1}D(w_i^{(l)}) Ml−1D(wi(l)) 倍,如下图所示:

由于均值为0,而方差越来越小,因此到后面的层,输出值会变得极小,不利于参数更新。对于梯度计算,同理有:
∂ L ∂ w i ( l ) = ∂ L ∂ a ( l + 1 ) ⋅ w i ( l + 1 ) ⋅ a i ( l − 1 ) \frac{\partial L}{\partial w_i^{(l)}} = \frac{\partial L}{\partial a^{(l+1)}} \cdot w_i^{(l+1)} \cdot a_i^{(l-1)} ∂wi(l)∂L=∂a(l+1)∂L⋅wi(l+1)⋅ai(l−1)
因此 D ( ∂ L ∂ w ( l ) ) = D ( ∂ L ∂ a ( l + 1 ) ) ⋅ M l + 1 D ( w ( l ) ) ⋅ ∏ i = 1 l M l − 1 D ( w i ( l ) ) D ( a ( 0 ) ) D(\frac{\partial L}{\partial w^{(l)}}) = D(\frac{\partial L}{\partial a^{(l+1)}}) \cdot M_{l+1} D(w^{(l)})\cdot \prod_{i=1}^{l} M_{l-1}D(w_i^{(l)})D(a^{(0)}) D(∂w(l)∂L)=D(∂a(l+1)∂L)⋅Ml+1D(w(l))⋅i=1∏lMl−1D(wi(l))D(a(0))
因此梯度的取值也呈现跟神经元输出值一样的规律:
Xavier初始化
为了解决这个问题,Xavier Glorot 提出了 Xavier初始化 方法,核心思想就是 尽可能保持每个神经元的输入和输出的方差一致,根据神经元的连接数量来自适应地调整初始化分布的方差。
根据上面的计算, D ( a ( l ) ) = M l − 1 D ( w i ( l ) ) D ( a ( l − 1 ) ) D(a^{(l)}) = M_{l-1}D(w_i^{(l)})D(a^{(l-1)}) D(a(l))=Ml−1D(wi(l))D(a(l−1)),如果需要保持方差一致,那么:
M l − 1 D ( w i ( l ) ) = 1 ⇒ D ( w i ( l ) ) = 1 M l − 1 M_{l-1}D(w_i^{(l)}) = 1 \Rightarrow D(w_i^{(l)}) = \frac{1}{M_{l-1}} Ml−1D(wi(l))=1⇒D(wi(l))=Ml−11
上面的结论是基于正向传播,如果反向传播时也需要保持方差一致,那么又有 D ( w i ( l ) ) = 1 M l D(w_i^{(l)}) = \frac{1}{M_{l}} D(wi(l))=Ml1,作为折中,可以设置: D ( w i ( l ) ) = 2 M l − 1 + M l D(w_i^{(l)}) = \frac{2}{M_{l-1} + M_l} D(wi(l))=Ml−1+Ml2
如果用高斯分布初始化权重,那么初始权重应服从分布 N ( 0 , 2 M l − 1 + M l ) \mathcal{N}(0,\frac{2}{M_{l-1} + M_l}) N(0,Ml−1+Ml2)
如果用均匀分布初始化权重,由于均匀分布的方差 D ( x ) = ( b − a ) 2 12 D(x) = \frac{(b-a)^2}{12} D(x)=12(b−a)2,因此如果要使得分布的均值为0,方差为 2 M l − 1 + M l \frac{2}{M_{l-1} + M_l} Ml−1+Ml2,那么初始权重应服从分布 U [ − 6 M l − 1 + M l , 6 M l − 1 + M l ] \mathcal{U}[-\sqrt{\frac{6}{M_{l-1} + M_l}},\sqrt{\frac{6}{M_{l-1} + M_l}}] U[−Ml−1+Ml6,Ml−1+Ml6]
上述初始化参数可以直接用于tanh函数,因为tanh函数在零点附近近似于 f ( x ) = x f(x) =x f(x)=x;而在应用于sigmoid函数时,需要乘以缩放因子4,因为sigmoid函数在零点附近的斜率为 1 4 \frac{1}{4} 41
| 高斯分布 | 均匀分布 | |
|---|---|---|
| sigmoid激活函数 | N ( 0 , 2 × 16 M l − 1 + M l ) \mathcal{N}(0,\frac{2\times 16}{M_{l-1} + M_l}) N(0,Ml−1+Ml2×16) | U [ − 4 6 M l − 1 + M l , 4 6 M l − 1 + M l ] \mathcal{U}[-4\sqrt{\frac{6}{M_{l-1} + M_l}},4\sqrt{\frac{6}{M_{l-1} + M_l}}] U[−4Ml−1+Ml6,4Ml−1+Ml6] |
| tanh激活函数 | N ( 0 , 2 M l − 1 + M l ) \mathcal{N}(0,\frac{2}{M_{l-1} + M_l}) N(0,Ml−1+Ml2) | U [ − 6 M l − 1 + M l , 6 M l − 1 + M l ] \mathcal{U}[-\sqrt{\frac{6}{M_{l-1} + M_l}},\sqrt{\frac{6}{M_{l-1} + M_l}}] U[−Ml−1+Ml6,Ml−1+Ml6] |
Xavier Glorot 等人在文章中展示了使用Xavier初始化初始化后的效果:
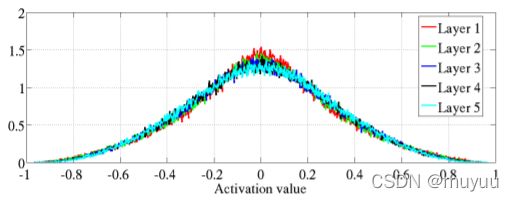
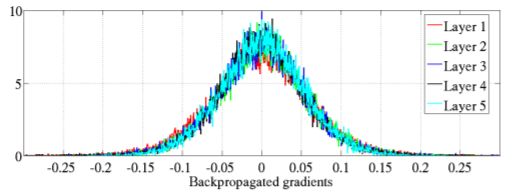
可以发现神经元输出值以及梯度值都改善了很多。
\quad
He初始化
上述初始化参数并不是适用于Relu激活函数,因为Relu函数有一边完全为零,因此方差应该近似于原来的一半,即
D ( a ( l ) ) = 1 2 M l − 1 D ( w i ( l ) ) D ( a ( l − 1 ) ) ⇒ D ( w i ( l ) ) = 2 M l − 1 D(a^{(l)}) = \frac{1}{2}M_{l-1}D(w_i^{(l)})D(a^{(l-1)}) \Rightarrow D(w_i^{(l)}) = \frac{2}{M_{l-1}} D(a(l))=21Ml−1D(wi(l))D(a(l−1))⇒D(wi(l))=Ml−12
但He初始化的提出者并没有考虑反向传播时的一致性,因此使用Relu激活函数时的参数初始化为:
| 高斯分布 | 均匀分布 | |
|---|---|---|
| Relu激活函数 | N ( 0 , 2 M l − 1 ) \mathcal{N}(0,\frac{2}{M_{l-1}}) N(0,Ml−12) | U [ − 6 M l − 1 , 6 M l − 1 ] \mathcal{U}[-\sqrt{\frac{6}{M_{l-1}}},\sqrt{\frac{6}{M_{l-1}}}] U[−Ml−16,Ml−16] |
正交初始化
除了上面那种通过控制均值和方差来控制参数范围的方法,另一种更直接的方式是 范数保持性。依然考虑激活函数为 f ( x ) = x f(x) =x f(x)=x,那么输入与输出的关系式为:
y = W ( L ) W ( L − 1 ) ⋯ W ( 1 ) x \boldsymbol y = \boldsymbol W^{(L)} \boldsymbol W^{(L-1)} \cdots \boldsymbol W^{(1)} \boldsymbol x y=W(L)W(L−1)⋯W(1)x
为了避免梯度消失或梯度爆炸问题,我们希望误差项在反向传播中具有 范数保持性,即
∣ ∣ a ( l ) ∣ ∣ = ∣ ∣ W ( l ) a ( l − 1 ) ∣ ∣ = ∣ ∣ W ( l ) ∣ ∣ ⋅ ∣ ∣ a ( l − 1 ) ∣ ∣ , ⇒ ∣ ∣ W ( l ) ∣ ∣ = 1 ||a^{(l)}|| = || \boldsymbol W^{(l)} a^{(l-1)}|| = || \boldsymbol W^{(l)}||\cdot|| a^{(l-1)}||,\Rightarrow || \boldsymbol W^{(l)}|| = 1 ∣∣a(l)∣∣=∣∣W(l)a(l−1)∣∣=∣∣W(l)∣∣⋅∣∣a(l−1)∣∣,⇒∣∣W(l)∣∣=1,即要求所有 W ( l ) \boldsymbol W^{(l)} W(l) 是正交矩阵。
正交初始化的具体实现过程可以分为两步:
- 用均值为 0、方差为 1的高斯分布初始化一个矩阵;
- 将这个矩阵用奇异值分解得到两个正交矩阵,并使用其中之一作为权重矩阵。
当在非线性神经网络中应用正交初始化时,通常需要将正交矩阵乘以一个缩放系数 ρ \rho ρ。比如当激活函数为ReLU时,激活函数在0附近的平均梯度可以近似为0.5。为了保持范数不变,缩放系数 ρ \rho ρ 可以设置为 2 \sqrt{2} 2.
##########################################################################
理解Dropout
dropout是深度学习中一种常用的正则化策略,它在训练阶段的每一次前向传播,让每个神经元以概率 p p p 停止工作,也就是说每次前向传播中,随机挑选 神经元总个数*p 数量的神经元并将其临时隐藏;在下一次前向传播,又将随机隐藏同样数量的另一批神经元,直至训练结束。
假设某个神经元的输出是 x x x ,期望是 E ( x ) E(x) E(x),那么加上dropout之后的期望变成了 E ( x ) ^ = ( 1 − p ) ∗ E ( x ) + p ∗ 0 \hat{E(x)}=(1-p)*E(x) + p*0 E(x)^=(1−p)∗E(x)+p∗0。由于测试阶段所有神经元总是被激活的,因此为了保持输出期望,我们需要将权重参数 w w w 乘以概率 1 − p 1-p 1−p 变成 ( 1 − p ) ∗ w (1-p)*w (1−p)∗w。但这样会加大测试时的计算量,影响测试性能。
通常为了提高测试的性能,可以将缩放的工作转移到训练阶段,而测试阶段维持原状,称为inverted dropout:将前向传播dropout时保留下来的神经元的权重乘上 1 1 − p \frac{1}{1-p} 1−p1,这样就维持了输出权重 E ( x ) ^ \hat{E(x)} E(x)^ 依旧为 E ( x ) E(x) E(x)。一般情况下, p p p 的取值范围在 0.2 ~ 0.5,输入层的 p p p 一般较小,避免丢失太多的输入信息,而隐藏层的 p p p 可以设置得大一些。
Dropout起作用的原因
-
集成学习角度:每做一次dropout,相当于从原始的网络中采样得到一个子网络。如果一个神经网络有 个神经元,那么总共可以采样出 2 n 2^n 2n 个子网络。每次迭代都相当于训练一个不同的子网络,而且由于每次迭代用到的batch不同,不同子网络训练的数据也跟bagging一样是替换采样的原始训练集的一个子集;但与bagging不同的是,dropout不会显示的将每一个子网络训练到收敛,但是这些子网络都共享原始网络的参数,这使得最终的网络也可以近似看作集成了指数级个不同网络的组合模型。
-
自适应破坏角度:dropout可以看作是对输入内容 自适应破坏 的一种形式,而不是对输入原始值的破坏。如果drop掉的神经元是几乎不提供信息的,那么其他神经元可以通过反向传播获得积极的信号;如果drop掉的神经元是比较有用的,例如代表了面部识别中鼻子的部分,那么丢失这个神经元对应于擦除图像中有鼻子的信息,这种情况下模型必须通过其他方式学习到这个特征,要么是鼻子存在的冗余编码,要么是脸部的另一特征,如嘴。而传统的噪声注入技术,在输入端加非结构化的噪声不能够随机地从脸部图像中抹去关于鼻子的信息,除非噪声的幅度大到几乎能抹去图像中所有的信息。
-
正则化角度:假设用深度学习处理一个回归问题,最后一个隐藏层有n个神经元,记它们的输出为 I 1 , ⋯ , I n I_1,\cdots,I_n I1,⋯,In,那么最终的损失函数是:
L = 1 2 ( y − ∑ i w i I i ) 2 L = \frac{1}{2}(y-\sum_i w_iI_i)^2 L=21(y−i∑wiIi)2
其中 y y y 是真实结果, w i w_i wi 是第i个神经元上的参数。而如果考虑dropout,则损失函数为:
L D = 1 2 ( y − ∑ i δ i w i I i ) 2 L_D = \frac{1}{2}(y-\sum_i \delta_i{w_i}I_i)^2 LD=21(y−i∑δiwiIi)2
其中 δ i \delta_i δi 满足分布 B e r n o u l l i ( p i ) Bernoulli(p_i) Bernoulli(pi)。由于dropout改变了输出期望,为了保持输出期望不变,我们将原始网络的每一个参数也乘以对应的伯努利参数 p p p,那么原始网络的损失函数变为:
L = 1 2 ( y − ∑ i p i w i I i ) 2 L = \frac{1}{2}(y-\sum_i p_i w_iI_i)^2 L=21(y−i∑piwiIi)2
对损失函数求导,分别有:
∂ L ∂ w i = − y p i I i + w i p i 2 I i 2 + ∑ j ≠ i w j p i p j I i I j \frac{\partial L}{\partial w_i} = -y p_i I_i + w_i p_i^2 I_i^2 + \sum_{j\neq i} w_j p_ip_j I_i I_j ∂wi∂L=−ypiIi+wipi2Ii2+j=i∑wjpipjIiIj
∂ L D ∂ w i = − y δ i I i + w i δ i 2 I i 2 + ∑ j ≠ i w j δ i δ j I i I j \frac{\partial L_D}{\partial w_i} = -y \delta_i I_i + w_i \delta_i^2 I_i^2 + \sum_{j\neq i} w_j \delta_i\delta_j I_i I_j ∂wi∂LD=−yδiIi+wiδi2Ii2+j=i∑wjδiδjIiIj
对 ∂ L D ∂ w i \frac{\partial L_D}{\partial w_i} ∂wi∂LD 求期望,得到:
E ( ∂ L D ∂ w i ) = − y E ( δ i ) I i + w i E ( δ i 2 ) I i 2 + ∑ j ≠ i w j E ( δ i ) E ( δ j ) I i I j = − y p i I i + w i V a r ( δ i ) I i 2 + w i p i 2 I i 2 + ∑ j ≠ i w j p i p j I i I j = ∂ L ∂ w i + w i V a r ( δ i ) I i 2 \begin{aligned} E(\frac{\partial L_D}{\partial w_i}) &= -y E(\delta_i) I_i + w_i E(\delta_i^2) I_i^2 + \sum_{j\neq i} w_j E(\delta_i)E(\delta_j) I_i I_j\\ &= -y p_i I_i + w_i Var(\delta_i) I_i^2 + w_i p_i^2 I_i^2 + \sum_{j\neq i} w_j p_ip_j I_i I_j\\ &= \frac{\partial L}{\partial w_i} + w_i Var(\delta_i) I_i^2 \end{aligned} E(∂wi∂LD)=−yE(δi)Ii+wiE(δi2)Ii2+j=i∑wjE(δi)E(δj)IiIj=−ypiIi+wiVar(δi)Ii2+wipi2Ii2+j=i∑wjpipjIiIj=∂wi∂L+wiVar(δi)Ii2
记:
L N = L + 1 2 w i 2 V a r ( δ i ) I i 2 L_N = L + \frac{1}{2}w_i^2 Var(\delta_i) I_i^2 LN=L+21wi2Var(δi)Ii2
那么 :
E ( ∂ L D ∂ w i ) = ∂ L N ∂ w i E(\frac{\partial L_D}{\partial w_i}) = \frac{\partial L_N}{\partial w_i} E(∂wi∂LD)=∂wi∂LN
仔细观察 L N L_N LN,发现 L N L_N LN = 原始的损失函数 + L2正则化项。也就是说,给网络加dropout等价于在损失函数中添加L2正则化项
再有,由于 δ i \delta_i δi满足伯努利分布,而伯努利分布的方差 V a r ( x ) = p ( 1 − p ) Var(x) = p(1-p) Var(x)=p(1−p),那么
L N = L + 1 2 w i 2 p i ( 1 − p i ) I i 2 L_N = L + \frac{1}{2}w_i^2 p_i(1-p_i) I_i^2 LN=L+21wi2pi(1−pi)Ii2
即,因此正则化项权重的最大值在 p i = 0.5 p_i = 0.5 pi=0.5 时取到,也就是说dropout值取0.5时,达到最大的正则化效果。当然后面会提到,dropout率越大,需要的网络就会越大,计算量和迭代次数也会相应增大,因此不能一味只考虑正则化的效果。
Dropout的使用限制
-
使用非常大的数据集时:虽然Dropout在特定模型上每一步的代价是微不足道的,但在一个完整的系统上使用Dropout的代价可能非常显著。因为Dropout是一个正则化技术,它减少了模型的有效容量。为了抵消这种影响,我们必须增大模型规模。例如,对于某个数据集最佳的层神经元个数是n,如果设置了dropout,drop率是p,那么为了弥补每次训练时drop掉的神经元,初始的层神经元个数应该设置为 n 1 − p \frac{n}{1-p} 1−pn。对于非常大的数据集,正则化带来的泛化误差减少得很小。在这些情况下,使用Dropout和更大模型的计算代价可能超过正则化带来的好处。
-
使用BatchNorm时:BatchNorm在训练时向隐藏单元引入加性和乘性噪声重新参数化模型。BatchNorm的主要目的是改善优化,但噪声具有正则化的效果,有时没必要再使用Dropout。
##########################################################################
归一化
归一化是深度学习一种常用的技巧,主要作用是提高训练效率。因为在深度模型的训练中,有以下两个问题会直接影响到模型的收敛速度:
- 随着参数更新,神经层的输入分布会发生变化,而且越深的层,其分布变化越明显。在前面的章节我们得知,神经元的方差总比上一层放缩 M l − 1 D ( w i ( l ) ) M_{l-1}D(w_i^{(l)}) Ml−1D(wi(l)) 倍:
D ( a ( l ) ) = ∏ l = 1 l M l − 1 D ( w i ( l ) ) D ( a ( 0 ) ) \begin{aligned} D(a^{(l)}) = \prod_{l=1}^{l} M_{l-1}D(w_i^{(l)})D(a^{(0)}) \end{aligned} D(a(l))=l=1∏lMl−1D(wi(l))D(a(0))这种情况称为 Interval Covariate Shift。 - 由于梯度的累乘性,随着层数的加深,层输出值容易进入激活函数的饱和区域,进而导致梯度消失等问题。
归一化针对性的处理了上述两个问题,有助于深度神经网络的训练。下面是两种常用的归一化方法:
Batch Normalization
归一化一般是作用于激活函数之前:
a ( l ) = f ( BN ( z ( l ) ) ) = f ( BN ( W a ( l − 1 ) ) ) \boldsymbol a^{(l)} = f(\text{BN}(\boldsymbol z^{(l)})) = f(\text{BN}(\boldsymbol W \boldsymbol a^{(l-1)})) a(l)=f(BN(z(l)))=f(BN(Wa(l−1)))
BN \text{BN} BN层的定义为:
BN ( z ( l ) ) = z ( l ) − μ B σ B 2 + ϵ ⊙ γ + β \text{BN}(\boldsymbol z^{(l)}) = \frac{\boldsymbol z^{(l)} - \boldsymbol \mu_B}{\sqrt{\boldsymbol \sigma_B^2 + \boldsymbol \epsilon}}\odot \boldsymbol \gamma + \boldsymbol \beta BN(z(l))=σB2+ϵz(l)−μB⊙γ+β
其中:
- μ B \boldsymbol \mu_B μB 是数据在batch上的均值, σ B 2 \boldsymbol \sigma_B^2 σB2 是数据在batch上的方差;用于将数据的每一维都归一到标准正态分布
- ϵ \boldsymbol \epsilon ϵ 是一个小值,用来防止除零操作
- γ \boldsymbol \gamma γ 和 β \boldsymbol \beta β 分别是缩放参数和平移参数;因为标准归一化会使得数据都集中在0附近,而这个取值区间刚好是接近激活函数的线性变换的区间,减弱了神经网络的非线性性质。因此通过添加缩放参数和平移参数让模型自适应调整输出值的区间范围。
不过论文 How Does Batch Normalization Help Optimization 中的实验表明:
- 没有证据表明 BN 能够起作用,是因为减少了Interval Covariate Shift
- BN 起作用的根本原因,是因为在网络的训练阶段,可以让大部分的激活函数能够远离其饱和区域,使得优化空间变的平滑
- 其他的 normalization 技术(例如 L1,L2),也能够像BN那样对于网络的训练起到作用
Layer Normalization
Batch Normalization对batch的大小比较敏感,此外,对于RNN这类净输入是不断变化的模型,Batch Normalization是无法使用的。而Layer Normalization则可用于处理这类情况。
Layer Normalization的定义与Batch Normalization类似:
h t = f ( LN ( z t ) ) = f ( LN ( U h t − 1 + W x t ) ) \boldsymbol h_t = f(\text{LN}(\boldsymbol z_t)) = f(\text{LN}(\boldsymbol U \boldsymbol h_{t-1} + \boldsymbol W \boldsymbol x_t)) ht=f(LN(zt))=f(LN(Uht−1+Wxt))
LN ( z t ) = z t − μ t σ t 2 + ϵ ⊙ γ + β \text{LN}(\boldsymbol z_t) = \frac{\boldsymbol z_t - \boldsymbol \mu_t}{\sqrt{\boldsymbol \sigma_t^2 + \boldsymbol \epsilon}}\odot \boldsymbol \gamma + \boldsymbol \beta LN(zt)=σt2+ϵzt−μt⊙γ+β
区别在于做归一化的维度不同:
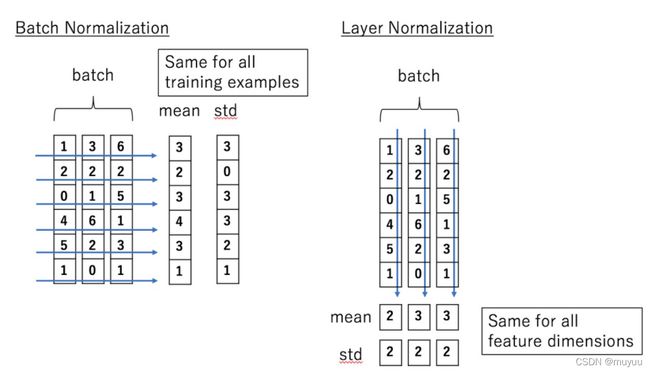
由上图可知,Batch Normalization是在batch维度上做归一化,而Layer Normalization是在step维度上做归一化。
Note,在实际使用时,
- 图片常使用Batch Norm,例如图片的尺寸是 (Batch * N * C),那么首选做切片得到 (Bathc * N *1),然后这个切片在batch维度上做归一化,也就是说在(1 * N * 1)这个向量上做归一化。
- 句子常使用Layer Norm,因为Batch中的每一个句子长度不一定一致,导致在batch维度上有的句子到后面的位置是空的。假设句子尺寸是 (Batch * seq_len * embed_size),首选切片得到 (1* seq_len* embed_size),然后这个切片在seq_len维度上做归一化,也就是说在(1 * 1 * embed_size)这个向量上做归一化。
Reference:
4. 参数初始化