论文笔记:NeRF++(2020)
文章目录
- 解决什么问题?有什么贡献
-
- shape与radiance之间是有可能存在歧义性的
- NeRF在大尺度场景下存在什么问题?
- 怎么解决的?
-
- 分析:NeRF的潜在失效情况及其的处理方式
- inverted sphere parameterization: 一种能够使得NeRF在unbounded场景下工作的参数化机制
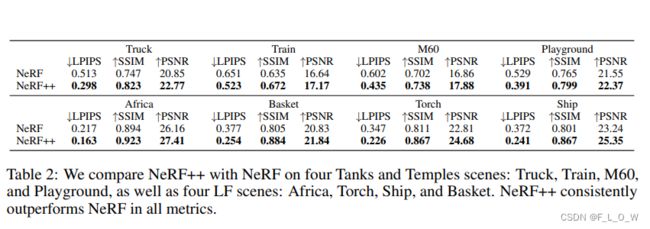
- 效果如何
论文链接:https://arxiv.org/pdf/2010.07492.pdf
解决什么问题?有什么贡献
首先对辐射场中的形状与辐射量之间的歧义性进行了分析,并且分析得到说那为什么NeRF可以避免这种歧义性。
第二,将原始的NeRF扩展到一个大尺度无边界的场景中。在这一点中,主要是通过将场景划分为前景与背景来实现的。
shape与radiance之间是有可能存在歧义性的
在一系列训练图像中,优化一个5D函数,在不加任何正则化的情况下,有可能会面临退化解的问题,也就进一步的导致了在新视角生成时潜在的failure cases。这种情况我们将其命名为 shape–radiance歧义性,示意图见下:

具体来说,对于不正确的场景几何 S ^ \hat{S} S^,训练影像也可以蛮好的fit(主要是通过view-dependent的radiance,来实现真实几何所能体现出来的视觉效果)。
而NeRF对这种歧义性进行了较好的处理。在后续的介绍中将会详细提及。
NeRF在大尺度场景下存在什么问题?
对于NeRF来说,要么仅仅只能再volume中fit场景中较小的一部分,完全抛弃背景的元素,要么就会对volume中大部分都去进行fit,但是会导致整体的细节信息都有所欠缺。
因此,文章通过一种简单但有效的方式对这个问题进行解决,即,将场景划分为前景与背景。
示意图见下:

怎么解决的?
分析:NeRF的潜在失效情况及其的处理方式
先回顾下NeRF在视角下进行优化的数学表达:
min σ , c 1 n ∑ i = 1 n ∥ I i − I ^ i ( σ , c ) ∥ 2 2 \min _{\sigma, \mathbf{c}} \frac{1}{n} \sum_{i=1}^{n}\left\|I_{i}-\hat{I}_{i}(\sigma, \mathbf{c})\right\|_{2}^{2} σ,cminn1i=1∑n∥ ∥Ii−I^i(σ,c)∥ ∥22
当给定射线: r = o + t d r = o + td r=o+td时,这条射线在影像上的颜色可以表达为:
C ( r ) = ∫ t = 0 ∞ σ ( o + t d ) ⋅ c ( o + t d , d ) ⋅ e − ∫ s = 0 t σ ( o + s d ) d s d t \mathbf{C}(\mathbf{r})=\int_{t=0}^{\infty} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=0}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t C(r)=∫t=0∞σ(o+td)⋅c(o+td,d)⋅e−∫s=0tσ(o+sd)dsdt
为了补偿网络的spectral bias【什么意思?】,以及合成更加锐利的影像,NeRF使用了位置编码,具体为:
γ k : p → ( sin ( 2 0 p ) , cos ( 2 0 p ) , sin ( 2 1 p ) , cos ( 2 1 p ) , … , sin ( 2 k p ) , cos ( 2 k p ) ) \gamma^{k}: \mathbf{p} \rightarrow\left(\sin \left(2^{0} \mathbf{p}\right), \cos \left(2^{0} \mathbf{p}\right), \sin \left(2^{1} \mathbf{p}\right), \cos \left(2^{1} \mathbf{p}\right), \ldots, \sin \left(2^{k} \mathbf{p}\right), \cos \left(2^{k} \mathbf{p}\right)\right) γk:p→(sin(20p),cos(20p),sin(21p),cos(21p),…,sin(2kp),cos(2kp))
其中, k k k是一个超参数,用了指定Fourier特征向量的维度。
可以想到,在没有正则化限制的前提下,形状和radiance之间是存在歧义性的,如下图所示:
我们来假设两种可能性:
(1)不正确的几何会使得辐射场有着更高的内在复杂性,或者说有着更高的频率;具体来讲, σ \sigma σ是由正确的几何形状导出的,那么 c \mathbf{c} c必须是关于 d \mathbf{d} d的高频函数【怎么理解?】。对于正确的形状来说,表面光场会相对来说光滑一些(比如说经典的朗伯体材质)。而对于不正确的形状来说,有用一个有限容量的MLP去表达appearance,就会是一件更难的事情。
(2)NeRF特殊的MLP结构隐式的编码了一个基于表面反射率的BRDF先验。下图是NeRF对radiance c \mathbf{c} c进行建模的简易示意图:
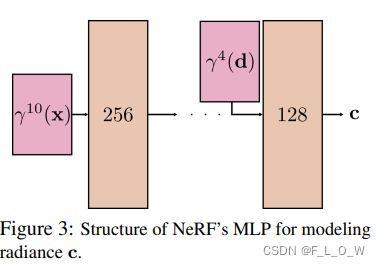
通常来说,MLP会更倾向于编码一个平滑的表面反射率函数,也就是说,对于给定的表面点 x \mathbf{x} x来说, c \mathbf{c} c与 d \mathbf{d} d之间的拟合关系会倾向于平滑。为什么会说倾向于平滑呢,我们可以从Figure3中看到,对于 d \mathbf{d} d的编码仅仅到四阶,再一个是从 d \mathbf{d} d的输入到最后的输入之间所包含的神经元并不多,也就意味着拟合能力会比较一般。
为了验证这种假设,我们做了一个实验:同等的对待变量 x \mathbf{x} x以及 d \mathbf{d} d,都将其位置编码到10阶,都在第一层进行输入。
做的对比实验结果如下所示:

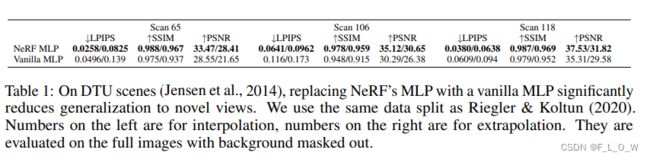
可以看到,所谓的vanilla MLP的测试效果并不如NeRF MLP,因此,侧面的验证了文章所提的假设,即,NeRF自身对反射模型做了正则化。
inverted sphere parameterization: 一种能够使得NeRF在unbounded场景下工作的参数化机制
我们知道,NeRF的体渲染积分,是在欧几里得深度上去做的。那么对于一些室外场景来说,比如建筑、山川、云等等,很可能会离得非常非常远。
这样一种高动态范围将会对NeRF的渲染效果产生巨大的影响。

我们是这样解决的:
首先将场景分为两个部分,一个是inner unit sphere,再一个是outer volume(使用所谓的inverted sphere) ,示意图见下:

在单位圆里,包含了前景以及相机,而其他的部分则包含了单位圆外。
这两个volume分别使用两个NeRF进行建模。为了渲染得到一条射线上的颜色,两个NeRF分别地进行渲染,最后再进行融合。对于内部的NeRF来说,不再需要重参数化,因为场景已经比较好的被包裹住了,而对于外部的NeRF来说,采用了一个所谓的inverted sphere parametrization。具体来说,一个外部的三维点 ( x , y , z ) , r = ( x 2 + y 2 + z 2 ) > 1 (x,y,z), r = \sqrt{(x^2 + y^2 +z^2)} >1 (x,y,z),r=(x2+y2+z2)>1将被重参数化为一个四元变量: ( x ′ , y ′ , z ′ , 1 / r ) , x ′ 2 + y ′ 2 + z ′ 2 = 1 \left(x^{\prime}, y^{\prime}, z^{\prime}, 1 / r\right), \quad x^{\prime 2}+y^{\prime 2}+z^{\prime 2}=1 (x′,y′,z′,1/r),x′2+y′2+z′2=1。其中, ( x ′ , y ′ , z ′ ) \left(x^{\prime}, y^{\prime}, z^{\prime}\right) (x′,y′,z′)是单位圆上的点,主要用于表达背景三维点的方向,而 r r r则是用来表现三维点 r ⋅ ( x ′ , y ′ , z ′ ) r \cdot (x ',y',z') r⋅(x′,y′,z′)的长度,那么 1 / r 1/r 1/r自然就是距离的倒数。
特别值得注意的是,四元变量的每一个值都是有界的,即:
x ′ , y ′ , z ′ ∈ [ − 1 , 1 ] , 1 / r ∈ [ 0 , 1 ] x^{\prime}, y^{\prime}, z^{\prime} \in[-1,1], 1 / r \in[0,1] x′,y′,z′∈[−1,1],1/r∈[0,1]
这样不仅仅可以让数值收敛的更加稳定,还可以使得更远的物体有着更小的resolution。
这个四元变量实际上只有三个自由度,我们将直接使用这个变量去渲染得到像素颜色。
至于如何将前景与背景的颜色进行融合,我们现在不妨来考虑将射线 r = o + t d \mathbf{r} = \mathbf{o} + t \mathbf{d} r=o+td划分为两个部分,对于第一部分来说, t ∈ ( 0 , t ′ ) t \in (0, t') t∈(0,t′)在单位球内,而对于第二个部分来说, t ∈ ( t ′ , ∞ ) t \in (t', \infin) t∈(t′,∞)在单位球外。
此时,我们就可以将体渲染公式改写为:
C ( r ) = ∫ t = 0 t ′ σ ( o + t d ) ⋅ c ( o + t d , d ) ⋅ e − ∫ s = 0 t σ ( o + s d ) d s d t ⏟ (i) + e − ∫ s = 0 t ′ σ ( o + s d ) d s ⏟ (ii) ⋅ ∫ t = t ′ ∞ σ ( o + t d ) ⋅ c ( o + t d , d ) ⋅ e − ∫ s = t ′ t σ ( o + s d ) d s d t ⏟ (iii) . \begin{aligned} \mathbf{C}(\mathbf{r})=& \underbrace{\int_{t=0}^{t^{\prime}} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=0}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{\text {(i) }} \\ &+\underbrace{e^{-\int_{s=0}^{t^{\prime}} \sigma(\mathbf{o}+s \mathbf{d}) d s}}_{\text {(ii) }} \cdot \underbrace{\int_{t=t^{\prime}}^{\infty} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=t^{\prime}}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{\text {(iii) }} . \end{aligned} C(r)=(i) ∫t=0t′σ(o+td)⋅c(o+td,d)⋅e−∫s=0tσ(o+sd)dsdt+(ii) e−∫s=0t′σ(o+sd)ds⋅(iii) ∫t=t′∞σ(o+td)⋅c(o+td,d)⋅e−∫s=t′tσ(o+sd)dsdt.
( i ) (i) (i)项以及 ( i i ) (ii) (ii)项,照常在欧几里得空间进行计算,而 ( i i i ) (iii) (iii)项则在inverted sphere space下进行积分,且以 1 r \frac{1}{r} r1为积分变量。
为了计算项 ( i i i ) (iii) (iii),我们需要用 1 r \frac{1}{r} r1来表示 ( x ′ , y ′ , z ′ ) (x',y',z') (x′,y′,z′),这样才能够用 ( x ′ , y ′ , z ′ , 1 r ) (x', y', z', \frac{1}{r}) (x′,y′,z′,r1)作为输入,以 σ o u t , c o u t \sigma_{out}, \mathbf{c}_{out} σout,cout作为输出。
见下图,射线与单位球在 a \mathbf{a} a点相交:
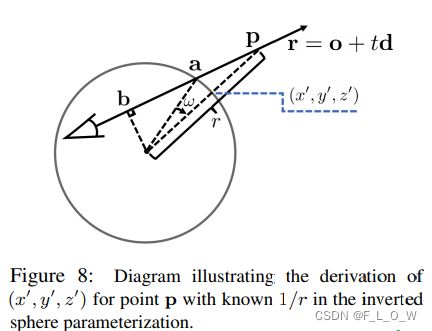
点 a = o + t a d \mathbf{a} = \mathbf{o} + t_a \mathbf{d} a=o+tad通过解求 ∣ o + t a d ∣ = 1 \left|\mathbf{o}+t_{a} \mathbf{d}\right|=1 ∣o+tad∣=1而得,而 b = o + t b d \mathbf{b} = \mathbf{o} + t_b \mathbf{d} b=o+tbd则通过解求 d T ( o + t b d ) = 0 \mathbf{d}^{T}\left(\mathbf{o}+t_{b} \mathbf{d}\right)=0 dT(o+tbd)=0得到。
在给定 1 r \frac{1}{r} r1的情况下,为了获得 ( x ′ , y ′ , z ′ ) (x',y',z') (x′,y′,z′),我们可以将向量 a \mathbf{a} a沿着向量 b × d \mathbf{b} \times \mathbf{d} b×d旋转 ω = arcsin ∣ b ∣ − arcsin ( ∣ b ∣ ⋅ 1 r ) \omega=\arcsin |\mathbf{b}|-\arcsin \left(|\mathbf{b}| \cdot \frac{1}{r}\right) ω=arcsin∣b∣−arcsin(∣b∣⋅r1)。
一旦我们能够在任何的 1 r \frac{1}{r} r1上都评估得到 σ o u t \sigma_{out} σout, c o u t \mathbf{c}_{out} cout,我们就可以在 [ 0 , 1 ] [0,1] [0,1]之间采样有限数量的点。
inverted sphere 参数化有着很直观的物理解释。
我们可以视作有一个虚拟的相机,其相机平面就是场景中心的单元球,因此,3D点 ( x , y , z ) (x,y,z) (x,y,z)可以投影到 ( x ′ , y ′ , z ′ ) (x', y', z') (x′,y′,z′),其中 1 r ∈ ( 0 , 1 ) \frac{1}{r} \in (0,1) r1∈(0,1)表示点的深度/视差。