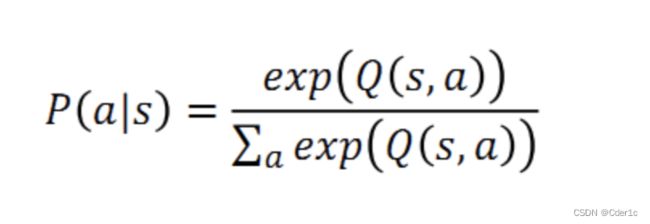Q-Learning, Double DQN与 Dueling DQN算法详解

参考学习课程

David Silver Reinforcement Learning
李宏毅教授强化学习

---

Value-based

Value-based 与 Policy-based的区别在上一篇文章有介绍，而Q-learning 是 value-based 的方法。在这种方法中我们不是要训练一个 policy，而是要训练一个critic网络。critic 并不直接采取行为，只是对现有的 actor $\pi$，评价它的好坏。

Q-Learning

算法思想

$Q$即为$Q(s,a)$就是在某一时刻的 $s(s\in S)$状态下，采取动作$a(a\in A)$动作能够获得收益的期望，环境会根据agent的动作反馈相应的回报reward $r$。算法的主要思想就是将State与Action构建成一张Q-table来存储$Q$值，然后根据$Q$值来选取能够获得最大的收益的动作。

Value Function

critic 给出了一个 value function $V^{\pi }(s)$，代表在遇到游戏的某个 state 后，采取策略为$\pi$的actor一直玩到游戏结束，所能得到的 reward 之和。

计算$V^{\pi }(s)$有两种方式

1. Monte-Carlo (MC) based approach
   
   将$S_a$作为$V^{\pi }$的输入并输出$V^{\pi }(S_a)$，而实际上应该得到的cumulative reward是$G_a$。我们的目标就是通过训练让 $V^{\pi }(S_a)$越来越接近$G_a$。
   MC 方法的问题在于最后得到的$G_a$的方差很大。$G_a$是在遇到$S_a$的情况下使用策略 $\pi$的actor一直玩游戏直到结束得到的实际 reward，是一个随机变量，因为游戏是有随机性的，所以每一次得到$G_a$是不一样的。
2. Temporal-difference (TD) approach
   
   MC-based的方法要求遇到$S_a$后把游戏玩到结束，如果游戏太长的话，那就可能收集不到多少数据去让网络去拟合$G_a$。而TD-based只需要从 $S_t$玩到$S_{t+1}$就行。
   在TD中，$V^{\pi }(S_t)=V^{\pi }(S_{t+1})+r_t$，我们的目标就是通过训练让$V^{\pi }(S_t)-V^{\pi }(S_{t+1})$越来越接近$r_t$。
   T方法f中有随机性的部分是 $r_t$，它的方差比较小。但TD的问题在于 $V^{\pi }(S_{t+1})$可能不准确。

Q Function

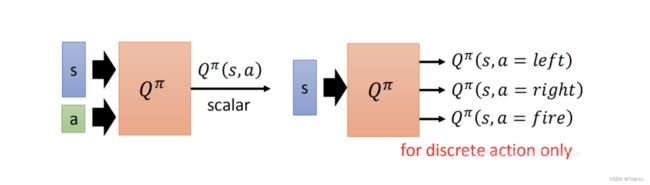
$Q^{\pi }(s,a)$的输入是一对$(s,a)$，然后输出一个cumulated reward的期望值。如果action可以穷举，则可以使用下图右边的写法；否则，使用左边的写法。

Q-learning的基本学习步骤是：

1. 使用一个初始的actor $\pi$与环境进行互动
2. 学习该actor对应的 Q function
3. 一定存在另外一个表现更好的${\pi }^{\prime }$，用这个更好的${\pi }^{\prime }$来替代原来的$\pi$
4. 重复上述步骤

更好的${\pi }^{\prime }$的定义是：面对所有 state $s$时，使用${\pi }^{\prime }$得到的value一定比使用策略$\pi$得到的大，即$V^{{\pi }^{\prime }}(s)\ge V^{\pi }(s)$
更新Q Function的公式：
$Q(s_t,a_t)=Q(s_t,a_t)+a(R_{t+1}+\lambda ma{x}_{a^{\prime }}Q(s_{t+1},a^{\prime })-Q(s_t,a_t))$
其中

1. $a$参数用来表示新的值对更新后值所造成的影响大小
2. $\gamma$是一个discount值

Q-learning的三个个小技巧

Target network

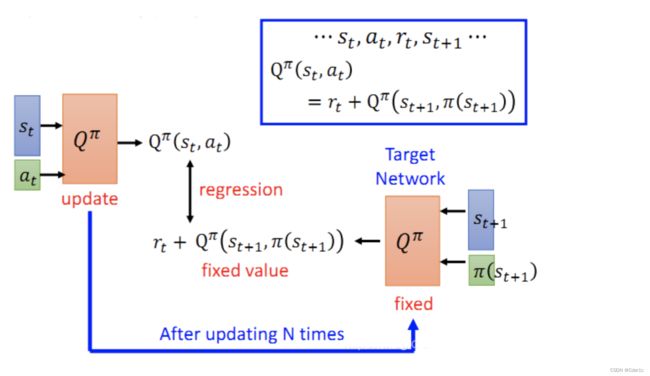
Q-function的训练，参考了TD的方法，即$Q^{\pi }(s_t,a_t)=Q^{\pi }(s_{t+1},\pi (s_{t+1}))+r_t$。但由于在训练的过程中，$s_{t+1}$和$\pi (s_{t+1})$是不断变化的，训练会比较困难。
所以：

1. 将以$s_{t+1}$、$a_{t+1}$作为输入的网络(Target network)固定住，这样$r_t+Q^{\pi }(s_{t+1},\pi (s_{t+1}))$也变成一个固定的值，然后让以$s_t$、$a_t$作为输入的网络去拟合这个固定的值。
2. 经过N次训练后，将左边的网络的参数覆盖掉Target network，形成新的Target network

Exploration

对于Q Function，它是policy的基础，这会导致actor每次都会选择具有更大Q值的行动action，对于收集数据而言是一个弊端，因为有可能有一个概率比较小的action其实具有更大的reward，我们可以采用以下方法解决：

Epsilon Greedy

在采取action的时候，actor会有$1-ϵ$的概率选择使得Q值最大的$a$，随着训练时间变长，$ϵ$的值逐渐减小，在后期actor选择最大Q值对应的$a$才会变大。

Boltzmann Exploration

根据概率分布进行采样

Replay Buffer

流程：

1. 用$\pi$和环境互动
2. 将步骤1中互动得到的经验$(s_t,a_t,r_t,s_{t+1})$放入一个 buffer (放在buffer里面的经验来自不同的policy，当buffer满了的时候，移除旧的经验。)
3. 在每一次迭代中，学习并更新$Q^{\pi }(s,a)$(每次从buffer里面sample一个batch出来训练)
4. 找到一个比$\pi$更好的${\pi }^{\prime }$
5. 重复上述步骤

因为buffer里有采取不同policy的actor的exp，所以导致这个训练过程变成off-policy的。但是因为我们只用一个exp训练，并不是整个trajectory，所以off-policy也没关系。
这样的好处有：

1. 训练过程中与环境交互很耗时间，而Replay Buffer可以使得之前的actor的exp被反复利用到，减少很Env互动次数；
2. 增加数据多样性，降低batch内相关性，提高泛化性能，训练效果更好。

完整的Q-Learning

Double DQN

由于Q值总是基于使得Q最大的action得出的，因此会趋向于被高估，于是引入double DQN：

我们使用两个$Q$ function，一个用来选择行动action，另外一个用来计算Q值，通常会选择target network来作为另外一个用于计算$Q$值的$Q^{\prime }$ function.

1. 如果$Q$高估了$a$而被选择，Q’会给这个被选择的a一个合适的$Q值
2. 如果$Q’$会高估某个action $a$，这个action并不会被Q选择到

Dueling DQN

Dueling DQN做得唯一一件事就是改变了network的架构 。

其中：

1. $V(s)$: 表示静态环境，状态$s$所具有的价值.
2. $A(s,a)$: 表示在状态$s$下采取行动$a$时的Advantage Function

通常，在计算$A(s,a)$时，使用单个行动对应的Advantage Value减去在该状态下采取所有行动所获得的Advantage Value的平均值，因此，对于一个状态下的所有action，具有零和特征。(normalise 在和$V(s)$相加之间进行) 。同时，如果只需要通过改变$V(s)$的值就能改变某个状态下所有的$Q$

小技巧

Prioritized Experience Replay

之前在buffer中sample数据去训练network的时候，是无差别地sample每一笔数据，就是说没有偏向于sample哪些数据。

这样做的不足是：有时候因为sample到的某一笔训练数据质量不好，造成$Q(s_t,a_t)$估测的值和$r_t+Q(s_{t+1},a_{t+1})$的差距比较大(即TD error)。如果接下去还是无差别地sample每一笔数据，就会导致这些TD error比较大的情况没有得到更多更好的训练，就会导致Q network 在有些情况估值不准确。

使用Prioritized Reply后，对于那些会造成TD error的情况，就会倾向于sample更多相关的数据来训练network，使得network克服这个TD error。

N step bootstraping

MC是计算的在$s_t$之后直到episode结束的所有reward，TD是计算$s_t$到$s_{t+1}$的reward。

Multi-step这个方法结合了MC和TD各自的特点，将TD改为计算$s_t$到$s_{t+n}$，即由原来跳到下一个状态，改为跳到之后$n$个状态。

Noisy Net:

Noise on Action

Noise on Parameters

这个技术是为了改进exploration的。之前的exploration（epsilon greedy）是在action上做noise。而Noisy Net是在Q-function的参数上做noise。

在action上加noise，即epsilon-greedy，就算给出同一个state $s$,也会做出不同的action $a$，可能是按照Q-function的结果，也可能是以random得到的结果。这不符合实际的情况，因为实际上我们希望给出同一个state，都会做出同样的action。

而在Q-function的参数上加noise，因为在这个方法规定了只在一个episode开始前添加noise，不会在episode中途再增加noise，所以在episode中遇到同一个state都会做出同样的action。比如在一个episode中，遇到状态都采取$a_1$的action，在另一个episode遇到状态都采取$a_2$的action。

Distributional Q-function

使用同一policy的actor在同一个state采取同一个action，得到的cumulated reward是不同的，因为后续state具有随机性。它会呈现一个特定distribution，而Q-value就是这些分布取mean的结果。

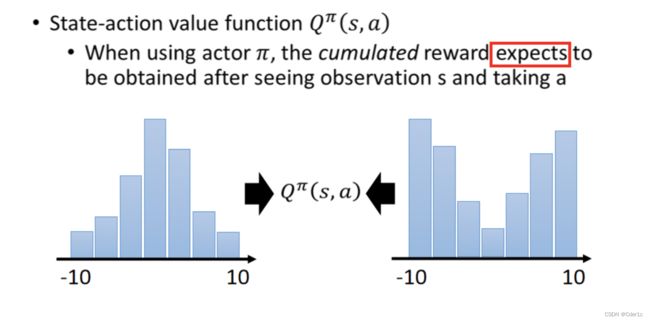
缺点：即便mean相同，但是可能实际的分布是完全不同的。然而因为Q-function只输出Q-value，所以看不到实际的分布。

解决方法：可以输出Q值的分布，当具有相同的均值时，选择具有较小方差（风险）的那一个，从而降低不稳定

比如下图右侧是Distributional Q-function，三种颜色代表三种action。同一颜色不同柱子代表在同一state下采取同一action产生的reward落在分布里的几率，具体来说，在绿色柱子里，5个柱子的X轴代表5种不同reward，Y轴代表在某一state采取某一action得到的reward落在此处的几率。