论文阅读【7】HHM隐马尔科夫模型
1.隐马尔科夫模型(HMM)的介绍
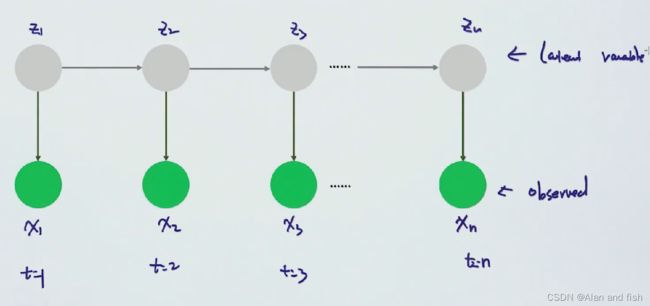
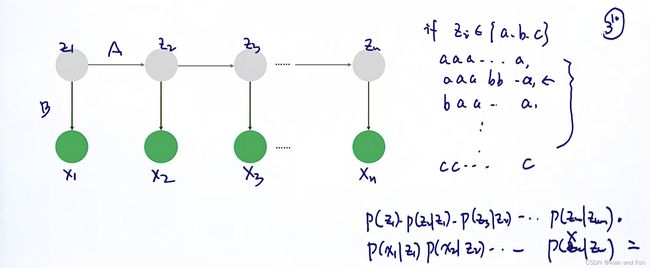
隐马尔科夫模型有两个序列,上面一层序列的值称之为影藏值(隐式变量),下面一个序列中的值被称为观察值,想这个的序列模型被称为生成模型(Generate model)。z表示的是一个状态,z所在的这条线上的箭头被称之为状态的转移,箭头表明转移的方向(Direction)。所以隐马尔科夫模型符合2个条件Dirction+Generate.
2.隐马尔科夫模型的深度理解
栗子1:硬币概率问题
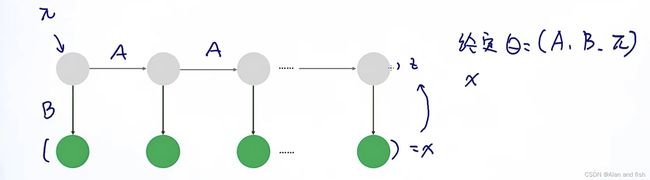
假设我手上有2种硬币,一个硬币叫做A,另外一个叫做B,但是这两个外观一样的硬币,但是出现的概率却不一样,A可能出现正面的概率是 μ 1 μ_1 μ1,B出现正面的概率是 μ 2 μ_2 μ2,所以 μ 1 μ_1 μ1和 μ 2 μ_2 μ2有可能相同也有可能不一样。
然后小明去扔硬币,我去观测硬币,小明负责扔硬币,我负责观测硬币,但是小明具体扔的是那一枚硬币我不知道,我只记录下我观测到的是正面还是反面。

因此这里面就可以提出2个问题:
- 问题1:究竟小明每次扔的是A还是B(推测问题)
- 问题2:扔A的概率 μ 1 μ_1 μ1是多少,扔B的概率 μ 2 μ_2 μ2是多少,并且扔完A之后扔B的概率是多少,生成了一个状态转移矩阵。(参数估算问题)
- 问题3:计算P(正反正…正)的概率,计算序列的概率(边缘概率问题)。
栗子2:词性标注任务
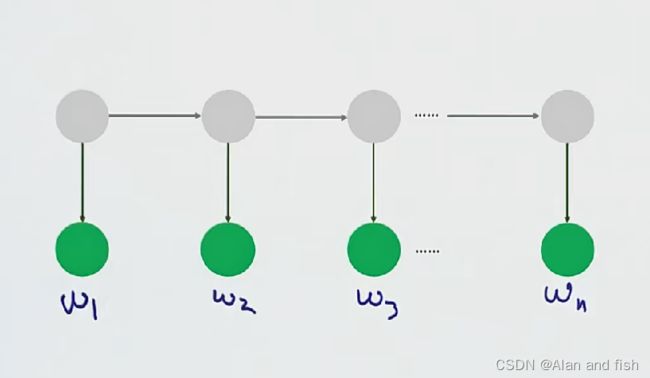
把绿色的看成我们观测到的单词,灰色的代表是这些单词的词性,是我们不知道的,所以这个任务就是推测出每个单词的词性是什么。因此也可以罗列出三个问题。
问题1:给定每个单词反推出每个单词的词性(inference、decoder),一般使用维特比算法去解决这个问题
问题2:参数估算问题,给定这一句话怎么去估计整个模型的参数。
问题3:计算 p ( w 1 , w 2 , . . . . . . w n ) p(w_1,w_2,......w_n) p(w1,w2,......wn)的概率,这是一个边缘概率,这个计算与序列有关,涉及到大量的计算,会使用动态规划算法。
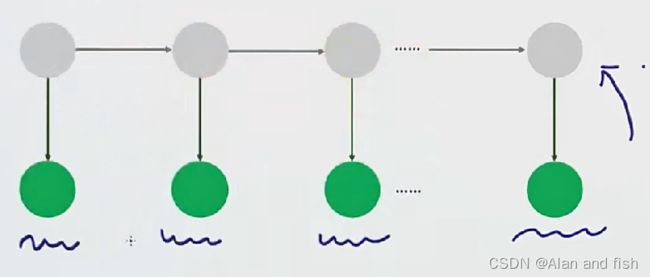
栗子3:语音识别问题
语音输入的是一条条的波形,则需要预测出这个一条条波形表达的背后的语义信息。
3.隐马尔科夫模型的参数问题
HMM模型 θ = ( A , B , π ) \theta=(A,B,π) θ=(A,B,π),对于模型中的数据我做了以下定义,观测变量为 x 1 , x 2 , x 3 . . . . . . . x n x_1,x_2,x_3.......x_n x1,x2,x3.......xn,隐式变量定义为 z 1 , z 2 , . . . . . . z n z_1,z_2,......z_n z1,z2,......zn.假设 z i z_i zi是离散型的
不懂就问:离散变量是指其数值只能用自然数或整数单位计算的则为离散变量。例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得。反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值.
- A代表状态转移矩阵,其中的每一行代表从状态c转移到状态i的概率,每一个值代表转移的每一个状态的概率,这一行中的概率之和为1.
- B代表生成(Emession)观测值的可能性。假设在一个隐式的状态下看到的观测值得概率是多少。其中的行向量中的每一列表示词库中每一个单词在i状态下的概率。
- π代表的是一个向量,其中的值为 π = [ π 1 π 2 π 3 π 4 π 5 π 6 ] π=[π_1 π_2 π_3 π_4 π_5 π_6] π=[π1π2π3π4π5π6],表示其中的某一个 z 1 z 2 . . . . z m z_1z_2....z_m z1z2....zm出现在第一个位置的概率是多少,概率之和为1.

问题1:能不能在给定x状态下估计出θ
问题2:在给定一个θ和某一个观测值X的情况下预测z
4.HMM中的inference问题
首先第一个问题就是,当我输入一个序列X之后如何去预测每个x所对应的标签,这就需要使用到维特比算法。
最笨的方法
假设需要每个x所对应的标签有3个, z i z_i zi属于{a,b,c},则把每一种可能出现的结果进行排列组合,那么可能得序列就会有 3 n 3^n 3n种结果,将所有序列罗列出来之后其实可以很好的计算这些序列的极大似然概率。
p ( z 1 ) p ( z 2 ∣ z 1 ) P ( z 3 ∣ z 2 ) . . . . . . . . . . . . P ( z n ∣ z n − 1 ) ∗ P ( x 1 ∣ z 1 ) P ( x 2 ∣ z 2 ) p ( x 3 ∣ z 3 ) . . . . . . . p ( x n ∣ z n ) p(z_1)p(z_2|z_1)P(z_3|z_2)............P(z_n|z_{n-1})*P(x1|z1)P(x_2|z_2)p(x_3|z_3).......p(x_n|z_n) p(z1)p(z2∣z1)P(z3∣z2)............P(zn∣zn−1)∗P(x1∣z1)P(x2∣z2)p(x3∣z3).......p(xn∣zn)
但是使用这种算法显而易见,计算量太大了。于是考虑使用下面一种方法,维特比算法。
维特比算法
维特比算法属于动态规划算法,对于那些复杂度是指数级计算的算法,使用一个中间变量,减轻其中的计算量。
将每个预测影藏值节点连接起来成一个图,则计算方式为
p = p ( z 1 = 2 ) p ( x 1 ∣ z 1 = 2 ) p ( z 2 = 1 ∣ z 1 = 2 ) p ( x 2 ∣ z 2 = 1 ) . . . . . . . . . . p=p(z_1=2)p(x_1|z_1=2)p(z_2=1|z_1=2)p(x_2|z_2=1).......... p=p(z1=2)p(x1∣z1=2)p(z2=1∣z1=2)p(x2∣z2=1)..........,当p的概率最大的时候就是最好的时候
使用维特比算法进行动态规划:
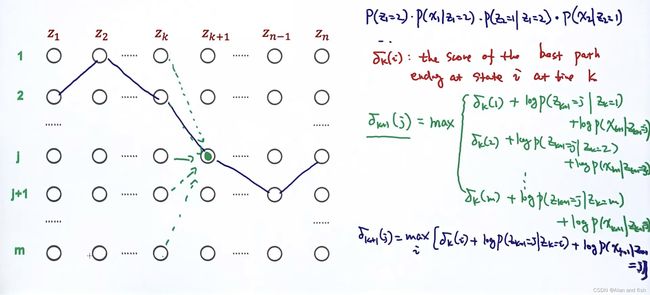
δ k ( i ) \delta_k(i) δk(i):在第k个时刻状态为i的时候的最好的路径。
则计算他的k+1个时刻的状态的概率,假设看k+1时候的值为J,则 δ k + 1 ( j ) \delta_{k+1}(j) δk+1(j)为下面式子的最大值max,用log就可以简化步骤:
δ k ( 1 ) + l o g p ( z k + 1 = j ∣ z k = 1 ) + l o g p ( x k + 1 ∣ z k + 1 = j ) ) \delta_k(1)+logp(z_{k+1}=j|z_k=1)+logp(x_{k+1}|z_{k+1}=j)) δk(1)+logp(zk+1=j∣zk=1)+logp(xk+1∣zk+1=j));
δ k ( 2 ) + l o g p ( z k + 1 = j ∣ z k = 2 ) + l o g p ( x k + 1 ∣ z k + 1 = j ) ) \delta_k(2)+logp(z_{k+1}=j|z_k=2)+logp(x_{k+1}|z_{k+1}=j)) δk(2)+logp(zk+1=j∣zk=2)+logp(xk+1∣zk+1=j));
…
δ k ( m ) + l o g p ( z k + 1 = j ∣ z k = m ) + l o g p ( x k + 1 ∣ z k + 1 = j ) ) \delta_k(m)+logp(z_{k+1}=j|z_k=m)+logp(x_{k+1}|z_{k+1}=j)) δk(m)+logp(zk+1=j∣zk=m)+logp(xk+1∣zk+1=j));
化简为一个递归的表示:
δ k + 1 ( i ) = m a x i [ δ k ( i ) + l o g p ( z k + 1 = j ∣ z k = i ) + l o g p ( x k + 1 ∣ z k + 1 = j ) ) ] \delta_{k+1}(i)=\underset{i}{max}[\delta_k(i)+logp(z_{k+1}=j|z_k=i)+logp(x_{k+1}|z_{k+1}=j))] δk+1(i)=imax[δk(i)+logp(zk+1=j∣zk=i)+logp(xk+1∣zk+1=j))];

所以基于上面的方法,从前往后依次计算每个状态的概率,并使用一个m*n的矩阵保存,然后将最大的值的路径也保存,这样就得到了最优的路径。
5.HMM的FB算法
FB算法的全程为(Forward and Backward)
他们分别的作用:
Forward:计算 p ( z k , x 1 : k ) p(z_k,x_{1:k}) p(zk,x1:k)的概率,其中 x 1 : k = ( x 1 , x 2 , x 3 . . . . . . . . x n ) x_{1:k}=(x_1,x_2,x_3........x_n) x1:k=(x1,x2,x3........xn)。
Backward:计算 p ( x k + 1 ∣ z k ) p(x_{k+1}|z_k) p(xk+1∣zk)的概率。
不懂就问:其中p(A,B)表示AB同时发生的概率,等同于p(AB),称之为联合概率分布
由于乘法法则知道: p ( Z k ∣ X ) = p ( Z k , X ) p ( X ) p(Z_k|X)={p(Z_k,X)\over p(X)} p(Zk∣X)=p(X)p(Zk,X) ∝ p ( Z k , x ) ∝p(Z_k,x) ∝p(Zk,x)
其中∝叫做正比符号(英文叫做proportion),因为上面的公式中的分母是不变的,变的是分子,所以可以直接看成求分子
p ( Z k , X ) = P ( X k + 1 : n ∣ Z k , X 1 : k ) ⋅ p ( Z k ⋅ X 1 : k ) p(Z_k,X)=P(X_{k+1:n}|Z_k,X_{1:k})·p(Z_k·X_{1:k}) p(Zk,X)=P(Xk+1:n∣Zk,X1:k)⋅p(Zk⋅X1:k)
如果 X 1 : k X_{1:k} X1:k独立于 X k + 1 : n X_{k+1:n} Xk+1:n则可以将 X 1 : k X_{1:k} X1:k省略掉,很显然他们是独立的,于是上式转换为:
p ( Z k , X ) = P ( X k + 1 : n ∣ Z k ) ⋅ p ( Z k , X 1 : k ) p(Z_k,X)=P(X_{k+1:n}|Z_k)·p(Z_k,X_{1:k}) p(Zk,X)=P(Xk+1:n∣Zk)⋅p(Zk,X1:k)
把上式的第一部分称为Backward,第二部分称之为Forward.

通过F/B算法,一方面可以计算出模型参数,这个是比较重要的一方面.
6.Forward 算法
这个算法的目标设计计算 p ( z k , x 1 : k ) p(z_k,x_{1:k}) p(zk,x1:k)的概率,详细计算过程如下图:

其中 x 1 : x − 1 , z k x_{1:x-1},z_k x1:x−1,zk是相关独立事件,可以都可以直接抵消掉.(实在有点检查不下去了,烂尾了,哈哈)
7.Backward算法
这个算法的目标就是计算 p ( x k + 1 : n ∣ z k ) p(x_{k+1:n}|z_k) p(xk+1:n∣zk)的概率.计算过程如下图:

总结
看到这一堆,是不是感觉脑袋都是大的,我确实也是的,看到最后脑袋也是变大了,最后 找到一个生动形象的例子:https://zhuanlan.zhihu.com/p/497045631
我总结一下这个HMM算法就是用已知去推导位置,首先要搞清楚几个概念,观测值,隐藏值,还有维特比算法(动态规划算法)