吴恩达机器学习python作业之单变量线性回归

第一个方法读取数据用的是pandas，第二个方法读数据用的是numpy。
第一种方法是梯度下降法，第二种方法是正规方程法。
跟着佬们的思路写写改改，如果有错误请私信或评论哦。
数据集理解：
ex1data1.txt的数据集是两列，第一列是population（自变量x），第二列是profit（因变量y），利用单变量线性回归进行拟合。

方法一：梯度下降法

参考链接：黄海广博士的github作业链接
https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes/blob/master/code/ex1-linear%20regression/ML-Exercise1.ipynb

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

#使用pandas包读取数据
dt = pd.read_csv("E:\机器学习\吴恩达\data_sets\ex1data1.txt",names = ["population" , "profit"] )

#读取的数据是pandas.DataFrame格式，将其转化为numpy.array格式
x_pd = dt["population"]
m = x_pd.size #97，是样本数
x = np.array(x_pd)
#(1, 97)
a = np.ones(m)



y_pd = dt["profit"]
y = np.array(y_pd)


#  #先进行绘图查看数据分布
plt.scatter(x,y)
# plt.show()

x = np.column_stack((a,x))
x = np.matrix(x)  #(97, 2)
#print(x.shape)
y = np.matrix(y)
y = y.T #(97, 1)
#print(y.shape)
theta = np.matrix(np.array([0,0])) #(1,2)
print(theta.shape[1])
#print(calculateCost(x,y,theta))
#print(type(theta)) #



#计算损失函数
def calculateCost(X,Y,theta):
    inner = np.power((X * theta.T - Y) , 2)
    return np.sum(inner / (2 * m))




def gradientDescent(X,Y,theta,alpha,iters,m):
    """
    实现梯度下降算法
    :param X: 1*97的矩阵，记录了各个城市的人口
    :param Y: 1*97的矩阵，记录了各个城市的利润
    :param theta: h(theta) = theta_1*x+theta_0
    :param alpha: 学习率
    :param iters: 迭代次数
    :param m:样本数
    :return: theta
    """
    result = np.matrix(np.zeros(theta.shape))
    for i in range(iters):
        #实现求导公式
        temp = X * theta.T - Y

        for j in range(2):
            inner = np.multiply(temp , X[:,j])
            result[0,j] = theta[0,j] - alpha * np.sum(inner) / m

        theta = result
    return theta

learningRate = 0.01
iterTimes = 1000
gg = gradientDescent(x,y,theta,learningRate,iterTimes,m)
#[[-3.24140214  1.1272942 ]]

print(calculateCost(x,y,gg))
#4.515955503078913

f = gg[0,0] + gg[0,1] * x

plt.plot(x,f,'r')
plt.show()

1.从txt文件中读取数据

#方法一：使用pandas包中的read_csv读取数据
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

#使用pandas包读取数据
dt = pd.read_csv("E:\机器学习\吴恩达\data_sets\ex1data1.txt",names = ["population" , "profit"] )

#读取的数据是pandas.DataFrame格式，将其转化为numpy.array格式
x_pd = dt["population"]
m = x_pd.size #97，是样本数
x = np.array(x_pd)
#(1, 97)
a = np.ones(m)


y_pd = dt["profit"]
y = np.array(y_pd)

#方法二：使用numpy包里的loadtxt函数
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

#使用pandas包读取数据
dt = np.loadtxt("E:\博士\学习资料\机器学习\吴恩达\data_sets\ex1data1.txt",delimiter=',')

#读取的数据是pandas.DataFrame格式，将其转化为numpy.array格式
x = dt[:,0]
m = len(x) #记录样本数
a = np.ones(m)

y = dt[:,1]

2.先用matplotlib查看数据集分布

#先进行绘图查看数据分布
plt.scatter(x,y)
# plt.show()

3.将array数据格式转换为matrix数据格式，方便后期进行矩阵运算

x = np.column_stack((a,x))
x = np.matrix(x)  #(97, 2)
#print(x.shape)
y = np.matrix(y)
y = y.T #(97, 1)
#print(y.shape)
theta = np.matrix(np.array([0,0])) #(1,2)
print(theta.shape[1])
#print(calculateCost(x,y,theta))
#print(type(theta)) #

4.利用矩阵运算计算损失函数

#计算损失函数
def calculateCost(X,Y,theta):
    inner = np.power((X * theta.T - Y) , 2)
    return np.sum(inner / (2 * m))

5.利用矩阵运算进行梯度下降算法的实现

def gradientDescent(X,Y,theta,alpha,iters,m):
    """
    实现梯度下降算法
    :param X: 1*97的矩阵，记录了各个城市的人口
    :param Y: 1*97的矩阵，记录了各个城市的利润
    :param theta: h(theta) = theta_1*x+theta_0
    :param alpha: 学习率
    :param iters: 迭代次数
    :param m:样本数
    :return: theta
    """
    result = np.matrix(np.zeros(theta.shape))
    for i in range(iters):
        #实现求导公式
        temp = X * theta.T - Y

        for j in range(2):
            inner = np.multiply(temp , X[:,j])
            result[0,j] = theta[0,j] - alpha * np.sum(inner) / m

        theta = result
    return theta

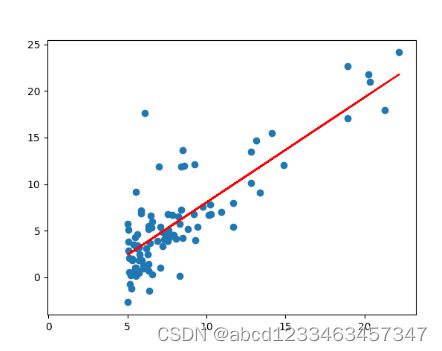
6.绘制曲线观察拟合程度

learningRate = 0.01
iterTimes = 1000
gg = gradientDescent(x,y,theta,learningRate,iterTimes,m)
#[[-3.24140214  1.1272942 ]]

print(calculateCost(x,y,gg))
#4.515955503078913

f = gg[0,0] + gg[0,1] * x

plt.plot(x,f,'r')
plt.show()

方法二：正规方程法

参考链接：
(7条消息) 吴恩达|机器学习作业1.0单变量线性回归_学吧学吧终成学霸的博客-CSDN博客

import numpy as np
from matplotlib import pyplot as plt

#1.读取数据并进行处理
dt = np.loadtxt("E:\博士\学习资料\机器学习\吴恩达\data_sets\ex1data1.txt",delimiter=",")
#dt类型：
#dt.shape:(97, 2)
#len(dt):97

cols = dt.shape[1]
#特征个数应该是前cols-1个
X = dt[:,0:cols - 1]
y = dt[:,-1]


#2.先可视化数据集，观察数据集的分布
plt.scatter(X,y)


#3.利用正规方程计算theta的值
m = X.shape[0]
a = np.ones((m,1)) #(97,1)
x = np.concatenate((a,X),1)
x_T = x.T
temp0 = np.linalg.inv(np.dot(x_T,x))
temp1 = np.dot(temp0,x_T)
theta = np.dot(temp1,y)
print(theta)

f = np.dot(x,theta)
plt.title("linear regression")
plt.xlabel("population")
plt.ylabel("profit")
plt.plot(X,f,"r")
plt.show()