计算机系统结构 第二章：缓存优化

计算机系统结构 第二章：缓存优化

三千红尘路，寥寥九州土
长安于我意何如
无关青云路，无关诗书
无你处，无江湖
——少司命《烟笼长安》

本章知识结构图：

缓存优化

存储器层次结构复习

Cache性能分析与改进

缓存优化:降低不命中率

缓存优化:减少不命中开销

缓存优化:减少命中时间

一、存储器层次结构复习

利用局部性原理组织存储器层次结构。

块（或行）是两级层次结构中信息交换的最小单元。

主存地址分割：$$【标识】【索引】【块内位移】$$
其中，标识和索引都属于块地址。
（低位）索引：选定对应的块（直接映射）或组（组相联），全相联没有索引。
（高位）标识：判断所选块，地址是否匹配。
块内位移：块大小为2^mB→m位块内位移。若存储器按字节编址，最低位还有2位字节偏移。

不同相联度下，Cache的结构图

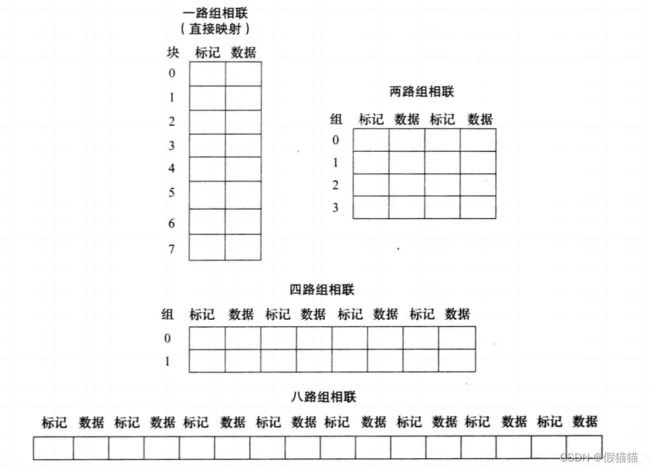
Cache的容量与索引（index），相联度，块大小的关系
$$Cache的容量=2^{index}\times 相联度\times 块大小$$

二、Cache性能分析与改进

平均访存时间与程序执行时间

$$平均访问时间=命中时间+不命中率\times 不命中开销$$
$$CPU时间=(CPU执行周期数+存储器停顿周期数)\times 时钟周期时间$$
$$\begin{array}{rl}存储器停顿时钟周期数& =“读”的次数\times 读不命中率\times 读不命中开销+“写”的次数\times 写不命中率\times 写不命中开销\\ & =访存次数\times 不命中率\times 不命中开销\end{array}$$
$$CPU时间=(CPU执行周期数+访存次数\times 不命中率\times 不命中开销)\times 时钟周期时间$$
$$\begin{array}{rl}CPU时间& =IC\times (CP{I}_{execution}+\frac{访存次数}{IC}\times 不命中率\times 不命中开销)\times 时钟周期时间\\ & =IC\times (CP{I}_{execution}+每条指令的平均访存次数\times 不命中率\times 不命中开销)\times 时钟周期时间\end{array}$$

Cache不命中对于一个CPI较小而时钟频率较高的CPU来说，影响是双重的：

• CPI_execution越低，固定周期数的Cache不命中开销的相对影响就越大。
• 在计算CPI时，不命中开销的单位是时钟周期数。因此，即使两台计算机的存储层次完全相同，时钟频率较高的CPU的不命中开销较大，其CPI中存储器停顿这部分也就较大。

因此，Cache对于低CPI、高时钟频率的CPU来说更加重要。

Cache性能改进

三个方面：

• 降低不命中率
• 减少不命中开销
• 减少Cache命中时间

三、缓存优化:降低不命中率

三种类型的不命中

• 强制性不命中(Compulsory miss)
  当第一次访问一个块时，该块不在Cache中，需从下一级存储器中调入Cache，这就是强制性不命中。 (冷启动不命中，首次访问不命中）

• 容量不命中(Capacity miss )
  如果程序执行时所需的块不能全部调入Cache中，则当某些块被替换后，若又重新被访问，就会发生不命中。这种不命中称为容量不命中。

• 冲突不命中(Conflict miss)
  在组相联或直接映像Cache中，若太多的块映像到同一组(块)中，则会出现该组中某个块被别的块替换(即使别的组或块有空闲位置)，然后又被重新访问的情况。这就是发生了冲突不命中。
  (碰撞不命中，干扰不命中)
  
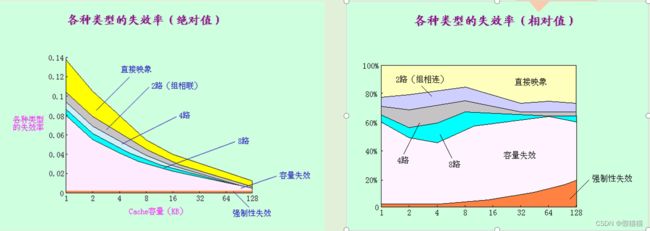
  观察到：

• 相联度越高，冲突不命中就越少；

• 强制性不命中和容量不命中不受相联度的影响；

• 强制性不命中不受Cache容量的影响，但容量不命中却随着容量的增加而减少。

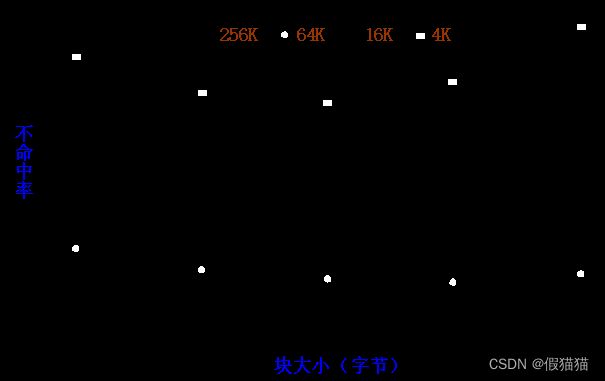
方法一：增加块大小（针对强制不命中）

• 对于给定的Cache容量，当块大小增加时，不命中率开始是下降，后来反而上升了。
• Cache容量越大，使不命中率达到最低的块大小就越大。（从上到下，曲线越来越平）

为什么不命中率先下降后上升？

• 一方面它减少了强制性不命中；（不命中率总体下降）
• 另一方面，由于增加块大小会减少Cache中块的数目，所以有可能会增加冲突不命中。（不命中率又升高了）

此外，增加块大小还会增加不命中开销。

方法二：增加Cache的容量（针对容量不命中）

针对容量不命中最直接的方法，缺点是增加成本，也可能增加命中时间。
这种方法多用于片外Cache。

方法三：提高相联度（针对冲突不命中）

• 采用相联度超过8的方案的实际意义不大。
• 2:1Cache经验规则：
  容量为N的直接映像Cache的不命中率和容量为N/2的两路组相联Cache的不命中率差不多相同。
• 提高相联度是以增加命中时间为代价。

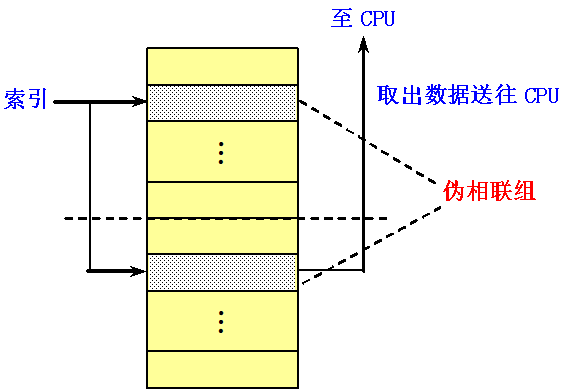
方法四：伪相联Cache

伪相联优点：命中时间小，不命中率低。这是结合了直接映像和组相联的优点。

基本思想及工作原理

• 在逻辑上把直接映像Cache的空间上下平分为两个区。
• 对于任何一次访问，伪相联Cache先按直接映像Cache的方式去处理。
  • 若命中，则其访问过程与直接映像Cache的情况一样。
  • 若不命中，则再到另一区相应的位置去查找。
    • 若找到，则发生了伪命中。
    • 否则就只好访问下一级存储器。
      

缺点 ：多种命中时间 – 快速命中与慢速命中。要保证绝大多数命中都是快速命中。
多种命中时间使CPU流水线设计复杂化，往往应用在离处理器较远的Cache上，如第二级Cache。

方法五：硬件预取

• 指令和数据都可以预取
• 预取内容既可放入Cache，也可放在外缓冲器中。例如：指令流缓冲器
• 指令预取通常由Cache之外的硬件完成
• 预取应利用存储器的空闲带宽，不能影响对正常不命中的处理，否则可能会降低性能。

方法六：编译器控制的预取

主要思想：在编译时加入预取指令，在数据被用到之前发出预取请求。

按照预取数据所放的位置，可把预取分为两种类型：

• 寄存器预取：把数据取到寄存器中。
• Cache预取：只将数据取到Cache中。

按照预取的处理方式不同，可把预取分为：

• 故障性预取：在预取时，若出现虚地址故障或违反保护权限，就会发生异常。
• 非故障性预取：在遇到这种情况时则不会发生异常，因为这时它会放弃预取，转变为空操作。本节假定Cache预取都是非故障性的，也叫做非绑定预取。

在预取数据的同时，处理器应能继续执行。只有这样，预取才有意义。这称为非阻塞Cache或非锁定Cache。

编译器控制预取的目的：使执行指令和读取数据能重叠执行。

循环是预取优化的主要对象

• 不命中开销小时：循环体展开1～2次
• 不命中开销大时：循环体展开许多次

每次预取需要花费一条指令的开销，保证这种开销不超过预取所带来的收益。
编译器可以通过把重点放在那些可能会导致不命中的访问上，使程序避免不必要的预取，从而较大程度地减少平均访存时间。

方法七：编译器优化

基本思想：通过对软件进行优化来降低不命中率。
（特色：无需对硬件做任何改动）

程序代码与数据重组

• 可以重新组织程序而不影响程序的正确性
  • 把一个程序中的过程重新排序，就可能会减少冲突不命中，从而降低指令不命中率。
    • McFarling研究了如何使用配置文件（profile）来进行这种优化。
  • 把基本块对齐，使得程序的入口点与Cache块的起始位置对齐，就可以减少顺序代码执行时所发生的Cache不命中的可能性。
• 如果编译器知道一个分支指令很可能会成功转移，那么它就可以通过以下两步来改善空间局部性：
  • 将转移目标处的基本块和紧跟着该分支指令后的基本块进行对调；
  • 把该分支指令换为操作语义相反的分支指令。
• 数据对存储位置的限制更少，更便于调整顺序。

编译优化技术

数组合并

内外循环交换

循环融合

分块

数组合并

将本来相互独立的多个数组合并成为一个复合数组，以提高访问它们的局部性。

内外循环交换

提高访问的局部性。

循环融合

将若干个独立的循环融合为单个的循环。这些循环访问同样的数组，对相同的数据作不同的运算。这样能使得读入Cache的数据在被替换出去之前，能得到反复的使用 。

分块

把对数组的整行或整列访问改为按块进行，尽量集中访问，减少替换，提高访问的局部性。例：

方法八：“牺牲”Cache

在Cache和它从下一级存储器调数据的通路之间设置一个全相联的小Cache，称为“牺牲”Cache（Victim Cache）。用于存放被替换出去的块(称为牺牲者)，以备重用。

“牺牲”Cache是一种能减少冲突不命中次数而又不影响时钟频率的方法。

作用：对于减小冲突不命中很有效，特别是对于小容量的直接映像数据Cache，作用尤其明显。例如项数为4的Victim Cache，能使4KB Cache的冲突不命中减少20%～90%。

四、缓存优化:减少不命中开销

方法一：两级Cache

第一级Cache(L1)小而快
第二级Cache(L2)容量大

性能分析：
$$平均访存时间=命中时{间}_{L1}+不命中{率}_{L1}\times 不命中开{销}_{L1}$$
$$不命中开{销}_{L1}=命中时{间}_{L2}+不命中{率}_{L2}\times 不命中开{销}_{L2}$$
$$平均访存时间=命中时{间}_{L1}+不命中{率}_{L1}\times (命中时{间}_{L2}+不命中{率}_{L2}\times 不命中开{销}_{L2})$$

局部不命中率和全局不命中率
$$局部不命中率=\frac{该级Cache的不命中次数}{到达该级Cache的访问次数}$$
例如上面式子中的不命中率_L2就是局部不命中率。
$$全局不命中率=\frac{该级Cache的不命中次数}{CPU发出的访存的总次数}$$
$$全局不命中{率}_{L2}=（局部）不命中{率}_{L1}\times （局部）不命中{率}_{L2}$$

全局不命中率比局部不命中率更有意义，它指出了在CPU发出的访存中，究竟有多大比例是穿过各级Cache，最终到达存储器的。

采用两级Cache时，每条指令的平均访存停顿时间：
$$每条指令的平均访存停顿时间=每条指令的平均不命中次{数}_{L1}\times 命中时{间}_{L2}+每条指令的平均不命中次{数}_{L2}\times 不命中开{销}_{L2}$$

注意：停顿时间中不包含命中时间_L1。

• 对于第二级Cache，我们有以下结论：
  • 在第二级Cache比第一级 Cache大得多的情况下，两级Cache的全局不命中率和容量与第二级Cache相同的单级Cache的不命中率非常接近。
  • 局部不命中率不是衡量第二级Cache的一个好指标，因此，在评价第二级Cache时，应用全局不命中率这个指标。
• 第二级Cache不会影响CPU的时钟频率，因此其设计有更大的考虑空间。
  • 设计第二级Cache时有两个问题需要权衡：
    • 它能否降低CPI中的平均访存时间部分？
    • 它的成本是多少？
• 第二级Cache的参数
  • 容量：第二级Cache的容量一般比第一级的大许多。
    • 大容量意味着第二级Cache可能实际上没有容量不命中，只剩下一些强制性不命中和冲突不命中。
  • 相联度：第二级Cache可采用较高的相联度或伪相联方法。

块大小

• 第二级Cache可采用较大的块，如 64、128、256字节
• 为减少平均访存时间，可以让容量较小的第一级Cache采用较小的块，而让容量较大的第二级Cache采用较大的块。

需要考虑的另一个问题：多级包容性（便于实现一致性检测）

• 第一级Cache中的数据是否总是同时存在于第二级Cache中。如果是，就说第二级Cache是具有多级包容性的。

方法二：让读不命中优先于写

Cache中的写缓冲器导致对存储器访问的复杂化:在读不命中时，所读单元的最新值有可能还在写缓冲器中，尚未写入主存。

解决问题的方法(读不命中的处理)

• 推迟对读不命中的处理，直到写缓冲器清空
  （缺点：读不命中的开销增加）
• 检查写缓冲器中的内容，若无相同，且存储器可用，继续处理读不命中（常用方案）

在写回法Cache中，也可采用写缓冲器。

方法三：写缓冲合并

• 提高写缓冲器的效率
• 写直达Cache依靠写缓冲来减少对下一级存储器写操作的时间。
  • 如果写缓冲器为空，就把数据和相应地址写入该缓冲器。从CPU的角度来看，该写操作就算是完成了。
  • 如果写缓冲器中已经有了待写入的数据，就要把这次的写入地址与写缓冲器中已有的所有地址进行比较，看是否有匹配的项。如果有地址匹配而对应的位置又是空闲的，就把这次要写入的数据与该项合并。这就叫写缓冲合并。
  • 如果写缓冲器满且又没有能进行写合并的项，就必须等待。
• 作用
  • 连续写入多个字的速度快于每次只写入一个字的操作；
  • 提高了写缓冲器的空间利用率，减少因写缓冲器满而要进行的等待时间。

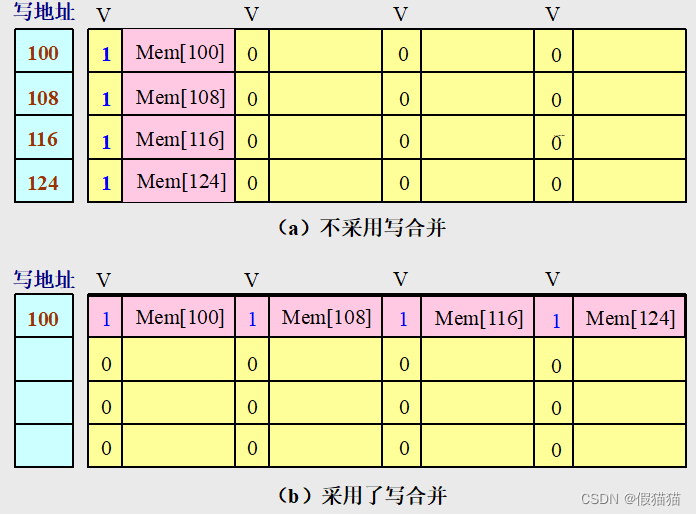
注意到，未采用写缓冲合并时，4次写入内容就填满了缓冲区，每个项目的四分之三被浪费。在为采用缓冲区时，图示上半部分右侧的字只会用于同时写多个字的指令。
也就是说，一个项（块）有多个字，一次写入操作很有可能只写入一个字，而项中的其余的字就可以用于提供合并。

方法四：请求字处理技术

• 请求字
  • 从下一级存储器调入Cache的块中，只有一个字是立即需要的。这个字称为请求字。
• 应尽早把请求字发送给CPU
  • 尽早重启动：请求字没有到达时，CPU处于等待状态。一旦请求字到达，立即送给CPU，让等待的CPU尽早重启动，继续执行。
  • 请求字优先：调块时，让存储器首先提供CPU所要的请求字。请求字一旦到达，就立即送给CPU，让CPU继续执行，同时从存储器调入该块的其余部分。
• 在以下情况下，用不用差别不大
  • Cache块较小
  • 下一条指令正好访问同一Cache块的另一部分

方法五：非阻塞Cache技术

• 非阻塞Cache：采用记分牌或者Tomasulo类控制方式，允许指令乱序执行，CPU无需在Cache不命中时停顿；
• 允许多次不命中，进一步提高性能；
• 可以同时处理的不命中次数越多，所能带来的性能上的提高就越大。
  • 但这并不意味着不命中次数越多越好。如对于整数程序来说，重叠次数对性能提高的影响不大，简单的“一次不命中下命中”就几乎可以得到所有的好处。
• 非阻塞Cache大大增加了Cache控制器的复杂度。特别是多重重叠的非阻塞Cache，更是如此。所以，在设计时要做全面综合的考虑。

五、缓存优化:减少命中时间

命中时间直接影响到处理器时钟频率的高低。在当今的许多计算机中，往往是Cache的访问时间限制了处理器的时钟频率。

方法一：使用小容量、结构简单的Cache

• 硬件越简单，速度就越快；
• 应使Cache足够小，以便可以与CPU一起放在同一块芯片上。
• 某些设计采用了一种折衷方案：把Cache的标识放在片内，而把Cache的数据存储器放在片外。
• 采用结构简单的Cache，比如直接映像Cache。

方法二：虚拟Cache

物理Cache

• 使用物理地址进行访问的传统Cache。
• 标识存储器中存放的是物理地址，进行地址检测也是用物理地址。
• 缺点：地址转换和访问Cache串行进行，访问速度很慢。

虚拟Cache

• 可以直接用虚拟地址进行访问的Cache。标识存储器中存放的是虚拟地址，进行地址检测用的也是虚拟地址。
• 优点：在命中时不需要地址转换，省去了地址转换的时间。即使不命中，地址转换和访问Cache也是并行进行的，其速度比物理Cache快很多。

虚拟Cache存在的问题

• 清空（purge）问题：由于新进程的虚拟地址可能与原进程相同；
• 解决方法：在地址标识中增加PID(进程标识符)字段；
• PID相关问题：为了减少位数，PID可能循环使用，所以也可能存在多个进程使用同一个PID，所以此时也需要清空Cache。

虚拟索引＋物理标识

• 原理：使用虚地址中的页内位移生成Cache索引；虚实转换后的实页地址作为标志tag
• 优点：兼得虚拟Cache和物理Cache的好处
• 局限性：Cache容量受到限制：Cache容量≤页大小×相联度

为什么之前情况下的Cache大小不受此限制？因为之前的物理Cache，索引位由Cache容量决定，剩余位均归于标识位。

方法三：Cache访问流水化

对第一级Cache的访问按流水方式组织：访问Cache需要多个时钟周期才可以完成。

实际上并不能真正减少Cache的命中时间，但可以提高访问Cache的带宽。

方法四：踪迹Cache

• 开发指令级并行性所遇到的一个挑战是：当要每个时钟周期流出超过4条指令时，要提供足够多条彼此互不相关的指令是很困难的。

• 一个解决方法：采用踪迹 Cache
  存放CPU所执行的动态指令序列，包含了由分支预测展开的指令，该分支预测是否正确需要在取到该指令时进行确认。

• 缺点
  地址映像机制复杂；
  相同的指令序列有可能被当作条件分支的不同选择而重复存放；

• 优点
  能够提高指令Cache的空间利用率。

Cache优化技术总结

“＋”号：表示改进了相应指标。
“－”号：表示它使该指标变差。
空格栏：表示它对该指标无影响。
复杂性：0表示最容易，3表示最复杂。

优化技术	不命中率	不命中开销	命中时间	硬件复杂度	说明
增加块大小	+	-		0	实现容易；Pentium 4 的第二级Cache采用了128字节的块
增加Cache容量	+		-	1	被广泛采用，特别是第二级Cache
提高相联度	+			1	被广泛采用
牺牲Cache	+			2	AMD Athlon采用了8个项的Victim Cache
伪相联Cache	+			2	MIPS R10000的第二级Cache采用
硬件预取指令和数据	+			2~3	许多机器预取指令，UltraSPARC Ⅲ预取数据
编译器控制的预取	+			2~3	需同时采用非阻塞Cache；有几种微处理器提供了对这种预取的支持
用编译技术减少Cache不命中次数	+			0	向软件提出了新要求；有些机器提供了编译器选项
使读不命中优先于写		+	-	1	在单处理机上实现容易，被广泛采用
写缓冲合并		+		1	与写直达合用，广泛应用，例如21164，UltraSPARC Ⅲ
尽早重启动与关键字优先		+		2	被广泛采用
非阻塞Cache		+		3	在支持乱序执行的CPU中使用
两级Cache			+	2	硬件代价大；两级Cache的块大小不同时实现困难；被广泛采用
容量小且结构简单的Cache	-		+	0	实现容易，被广泛采用
对Cache进行索引时不必进行地址变换			+	2	对于小容量Cache来说实现容易，已被Alpha 21164和UltraSPARC Ⅲ采用
流水化Cache访问			+	1	被广泛采用
踪迹Cache			+	3	Pentium 4 采用

练习题

填空题

1.增加cache容量的方法多用于（ ）。
2.提高相联度是以（ ）为代价。
3.硬件预取可以预取（ ）和（ ），预取内容既可放入（ ），也可放入（ ）中。指令预取通常由（ ）的硬件完成。
4.按照预取数据所放的位置，可把预取分为（ ）和（ ）；按照预取的处理方式不同，可把预取分为（ ）和（ ）。
5.cache访问流水化是对第（ ）级cache按流水化方式组织。

1.片外Cache
2.增加命中时间
3.指令 数据 Cache 外缓冲器 Cache之外
4.寄存器预取 Cache预取 故障性预取 非故障性预取
5.一

问答题

1. 说明Cache不命中对于一个CPI较小而时钟频率较高的CPU来说的双重影响。

• CPI_execution越低，固定周期数的Cache不命中开销的相对影响就越大。
• 在计算CPI时，不命中开销的单位是时钟周期数。因此，即使两台计算机的存储层次完全相同，时钟频率较高的CPU的不命中开销较大，其CPI中存储器停顿这部分也较大。

2. 可以从哪三个方面改进Cache的性能？

降低不命中率，减少不命中开销，减少命中时间。

3. 三种类型的不命中分别是什么？请简要概述。

• 强制不命中：当第一次访问一个块时，该块不在Cache中，需从下一级存储器中调入Cache，这就是强制不命中。
• 容量不命中：如果程序执行时所需的块不能全部调入Cache中，则当某些块被替换后，若又重新被访问，就会发生不命中。这种不命中称为容量不命中。
• 冲突不命中：在组相联或直接映像Cache中，若太多的块映像到同一组（块）中，则会出现该组中某个块被别的块替换（即使别的组或块有空闲位置），然后又被重新访问的情况。这就是发生了冲突不命中。

4. cache的相联度和容量分别会影响哪种不命中？

相联度会影响冲突不命中。
容量会影响容量不命中。

5. 写出8种用于降低不命中率的cache优化技术。

增加块大小；增加Cache容量；提高相联度；伪相联Cache；硬件预取；编译器预取；编译器优化；牺牲Cache。

6. 写出5种用于减少不命中开销的cache优化技术。

两级Cache；让读不命中优先于写；写缓冲合并；请求字处理技术；非阻塞Cache技术。

7. 写出4种用于减少命中时间的cache优化技术。

使用小容量、结构简单的Cache；虚拟Cache；Cache访问流水化；踪迹Cache。

8. 为什么增加块大小，不命中率先下降后上升？

• 一方面它减少了强制性不命中；（不命中率总体下降）
• 另一方面，由于增加块大小会减少Cache中块的数目，所以有可能会增加冲突不命中。（不命中率又升高了）

9. 简述2:1Cache经验规则。

容量为N的直接映像Cache的不命中率和容量为N/2的两路组相联Cache的不命中率差不多相同。

10. 伪相联cache的优点是什么？

命中时间小，不命中率低。

11. 简述伪相联cache的基本工作原理。

• 在逻辑上吧直接映像Cache的空间上下平分为两个区。
• 对于任何一次访问，伪相联Cache先按直接映像Cache的方式去处理。
  • 若命中，则其访问过程与直接映像Cache的情况一样。
  • 若不命中，则再到另一区相应的位置去查找。
    • 若找到，则发生了伪命中。
    • 否则就只好访问下一级存储器。

12. 硬件预取应该建立在什么样的基础上？否则，可能会出现哪些问题？

预取应利用存储器的空闲带宽，不能影响对正常不命中的处理，否则可能会降低性能。

13. 编译器控制预取的目的是什么？

使执行指令和读取数据能重叠执行。

14. 编译优化技术包括哪些？

数组合并；内外循环交换；循环融合；分块。

15. 如果编译器知道一个分支指令很可能会成功转移，那么它就可以通过什么来改善空间局部性？

使大概率执行的代码放在分支失败处：

• 将转移目标处的基本块和紧跟着该分支指令后的基本块进行对调；
• 把该分支指令换为操作语义相反的分支指令。

16. 简述数组合并的基本思想。

将本来相互独立的多个数组合并称为一个复合数组，以提高访问他们的局部性。

17. 简述循环融合的基本思想。

将若干个独立的循环融合为单个的循环。这些循环访问同样的数组，对相同的数据作不同的运算。这样能使得读入Cache的数据在被替换出去之前，能得到反复的使用。

18. 简述“牺牲”cache的基本思想。

在Cache和它从下一级存储器调数据的通路之间设置一个全相联的小Cache，称为“牺牲”Cache。用于存放被替换出去的块，以备重用。

19. 简述cache多级包容性的概念。

第一级Cache中的数据是否总是同时出现在第二级Cache中。如果是，就说第二级Cache是具有多级包容性的。

20. 简述让读不命中优先于写的方法。

• 推迟对读不命中的处理，直到写缓冲器清空。
• 检查写缓冲器的内容，若无相同，继续处理读不命中。

21. 简述写缓冲合并下一次写操作的过程。

• 如果写缓冲器为空，就把数据和相应地址写入该缓冲器。从CPU的角度来看，该写操作就算是完成了。
• 如果写缓冲器中已有待写入的数据，就要把这次的写入地址与写缓冲器中已有的所有地址进行比较，看是否有匹配的项。如果有地址匹配而对应的位置又是空闲的，就把这次要写入的数据与该项合并。
• 如果写缓冲器满且又没有能进行写合并的项，就必须等待。

22. 写缓冲合并的优点？

• 连续写入多个字的速度快于每次只写入一个字的操作；
• 提高了写缓冲器的空间利用率，减少因写缓冲器满而要进行的等待时间。

23. 简述请求字处理技术的两种方案。什么情况下，用不用该技术差别不大？

• 尽早重启动：请求字没有到达时，CPU处于等待状态。一旦请求字到达，立即送给CPU，让等待的CPU尽早重启动，继续执行。
• 请求字优先：调块时，让存储器首先提供CPU所要的请求字。请求字一旦到达，就立即送给CPU，让CPU继续执行，同时从存储器调入该块的其余部分。
• 在以下情况下，用不用差别不大：
  • Cache块较小
  • 下一条指令正好访问同一Cache的另一部分

24. 画出物理cache存储系统和虚拟cache存储系统的示意图。

25. 简述虚拟cache存在的问题。

由于新进程的虚拟地址和原进程可能相同，因此每当进行进程切换的时候需要清空Cache。
如果使用进程标识符字段（PID）区分进程，当PID重用时，也需要清空Cache。

26. 简述虚拟索引＋物理标识方法的原理和优缺点。

• 优点：兼得虚拟Cache和物理Cache的好处。
• 缺点：Cache容量收到限制。

27. 简述踪迹cache的原理和优缺点。

• 优点：
  • 能够提高指令Cache的空间利用率。
• 缺点：
  • 地址映像机制复杂。
  • 相同的指令序列有可能被当作条件分支的不同选择而重复存放。

计算题

1. 假设Cache不命中开销为50个时钟周期，当不考虑存储器停顿时，所有指令的执行时间都是2.0个时钟周期，访问Cache不命中率为2%，平均每条指令访存1.33次。试分析Cache对性能的影响。

$$\begin{array}{rl}CPU时{间}_{有Cache}& =IC\times (CP{I}_{execution}+每条指令的平均访存次数\times 不命中率\times 不命中开销)\times 时钟周期时间\\ & =IC\times (2+1.33\times 2\%\times 50)\times 时钟周期时间\\ & =3.33\times IC\times 时钟周期时间\end{array}$$
注意到，
$$每条指令的平均时钟周期数(CPI)=CPU时间÷指令数（IC）÷时钟周期时间$$
CPI_有Cache=3.33
3.33/2.0=1.67（倍）
故有Cache情况下，CPU时间为原来的1.67倍。
$$CP{I}_{无Cache}=2+1.33\times 50=68.5$$
68.5/2.0=34.25（倍）
故无Cache情况下，CPU时间为原来的34.25倍。

2. 考虑两种不同组织结构的Cache：直接映像Cache和两路组相联Cache，试问它们对CPU的性能有何影响？先求平均访存时间，然后再计算CPU性能。分析时请用以下假设：
   (1)理想Cache（命中率为100%）情况下的CPI为2.0，时钟周期为2ns，平均每条指令访存1.3次。
   (2)两种Cache容量均为64KB，块大小都是32字节。
   (3)在组相联Cache中，由于多路选择器的存在而使CPU的时钟周期增加到原来的1.10倍。这是因为对Cache的访问总是处于关键路径上，对CPU的时钟周期有直接的影响。
   (4) 这两种结构Cache的不命中开销都是70ns。（在实际应用中，应取整为整数个时钟周期）
   (5) 命中时间为1个时钟周期，64KB直接映像Cache的不命中率为1.4%，相同容量的两路组相联Cache的不命中率为1.0%。

$$\begin{array}{rl}平均访存时{间}_{直接映像Cache}& =命中时间+不命中{率}_{直接映像Cache}\times 不命中开销\\ & =1\times 2+1.4\%\times 70\\ & =2.98ns\end{array}$$
$$\begin{array}{rl}平均访存时{间}_{2路组相联Cache}& =命中时间+不命中{率}_{2路组相联Cache}\times 不命中开销\\ & =1.1\times 2+1\%\times 70\\ & =2.9ns\end{array}$$
2路组相联的平均访存时间较低。
$$\begin{array}{rl}CPU时{间}_{直接映像Cache}& =IC\times (CP{I}_{execution}+每条指令的平均访存次数\times 不命中{率}_{直接映像Cache}\times 不命中开销)\times 时钟周期时{间}_{直接映像Cache}\\ & =IC\times (2+1.3\times 1.4\%\times 35)\times 2\\ & =5.274\times IC\end{array}$$
2路组相联Cache的不命中开销为70ns/2.2=32个时钟周期时间。
$$\begin{array}{rl}CPU时{间}_{2路组相联Cache}& =IC\times (CP{I}_{execution}+每条指令的平均访存次数\times 不命中{率}_{2路组相联Cache}\times 不命中开销)\times 时钟周期时{间}_{2路组相联Cache}\\ & =IC\times (2+1.3\times 1\%\times 32)\times 2.2\\ & =5.315\times IC\end{array}$$
直接映像Cache的平均性能较好。

3. 假设当在按直接映象找到的位置处没有发现匹配，而在另一个位置才找到数据（伪命中）需要2个额外的周期。问：当Cache容量分别为2 KB和128 KB时，直接映象、2路组相联和伪相联这三种组织结构中，哪一种速度最快？
   Cache容量为2KB时，有：

	失效率	失效开销（周期）	平均访存时间（周期）
1路	0.098	50	5.90
2路	0.076	50	4.90

Cache容量为128KB时，1路、2路失效率分别为：0.010,0.007

	失效率	失效开销（周期）	平均访存时间（周期）
1路	0.010	50	1.50
2路	0.007	50	1.45

应该是可以默认直接命中时间为1个时钟周期。
根据伪相联Cache的工作原理分析：
$$\begin{array}{rl}平均访存时{间}_{伪相联}& =命中时{间}_{伪相联}+失效{率}_{伪相联}\times 失效开{销}_{伪相联}\\ 失效{率}_{伪相联}& =失效{率}_{2路}\\ 失效开{销}_{伪相联}& =失效开{销}_{1路}\\ 伪命中率& =命中{率}_{2路}-命中{率}_{1路}\\ & =(1-失效{率}_{2路})-(1-失效{率}_{1路})\\ & =失效{率}_{1路}-失效{率}_{2路}\end{array}$$
因此，$$平均访存时{间}_{伪相联}=命中时{间}_{1路}+(失效{率}_{1路}-失效{率}_{2路})\times 2+失效{率}_{2路}\times 失效开{销}_{1路}$$
Cache容量为2KB时，
$$平均访存时{间}_{伪相联}=1+(0.098-0.076)\times 2+0.076\times 50=4.844$$
Cache容量为128KB时，
$$平均访存时{间}_{伪相联}=1+(0.010-0.007)\times 2+0.007\times 50=1.356$$
因此，不论Cache容量为2KB还是128KB，三种结构中伪相联速度最快。

4. 考虑某一两级Cache：第一级Cache为L1，第二级Cache为L2。
   （1）假设在1000次访存中，L1的不命中是40次，L2的不命中是20次。求各种局部不命中率和全局不命中率。
   （2）假设L2的命中时间是10个时钟周期，L2的不命中开销是100时钟周期，L1的命中时间是1个时钟周期，平均每条指令访存1.5次，不考虑写操作的影响。问：平均访存时间是多少？每条指令的平均停顿时间是多少个时钟周期？

（1）
$$\begin{array}{r}局部不命中{率}_{L1}=\frac{40}{1000}=0.04\\ 全局不命中{率}_{L1}=\frac{40}{1000}=0.04\\ 局部不命中{率}_{L2}=\frac{20}{40}=0.5\\ 全局不命中{率}_{L2}=\frac{20}{1000}=0.02\end{array}$$
（2）
$$\begin{array}{rl}平均访存时间& =命中时{间}_{L1}+不命中{率}_{L1}\times (命中时{间}_{L2}+不命中{率}_{L2}\times 不命中开销)\\ & =1+0.04\times (10+0.5\times 100)=3.4\end{array}$$
$$每次访存的平均停顿时间：3.4-1=2.4$$
$$\begin{array}{rl}每条指令的平均停顿时间& =每次访存的平均停顿时间\times 每条指令的平均访存次数\\ & =2.4\times 1.5=3.6\end{array}$$

5. 给出有关第二级Cache的以下数据：
   （1）对于直接映像，命中时间L2 ＝ 10个时钟周期
   （2）两路组相联使命中时间增加0.1个时钟周期，即为10.1个时钟周期。
   （3） 对于直接映像，局部不命中率L2 ＝ 25%
   （4） 对于两路组相联，局部不命中率L2 ＝ 20%
   （5） 不命中开销L2 ＝ 50个时钟周期
   试问第二级Cache的相联度对不命中开销的影响如何？

$$\begin{array}{r}不命中开{销}_{直接映像,L1}=10+25\%\times 50=22.5\\ 不命中开{销}_{两路组相联,L1}=10.1+20\%\times 50=20.1\end{array}$$
对第二级Cache来说，两路组相联不命中开销较小。

6. 假定：
   (1) 使用一个容量为8 KB、块大小为16 B的直接映象Cache，它采用写回法并且按写分配。
   (2) a、b分别为3×100（3行100列）和101×3的双精度浮点数组，每个元素都是8B。当程序开始执行时，这些数据都不在Cache内。
   对于下面的程序：

           for （ i = 0 ;  i < 3 ;  i = i + 1 ）
                    for （ j = 0 ;  j < 100 ;  j = j + 1 ）
                           a [ i ][ j ] = b[ j ][ 0 ] * b[ j+1 ][ 0 ];  

问：
（1）判断哪些访问可能会导致数据Cache失效；
（2）加入预取指令以减少失效，设预取提前7次循环进行。
（3）计算所执行的预取指令的条数以及通过预取避免的失效次数。
（4）计算节省的时间。忽略指令缓存缺失，并假定数据缓存中没有冲突缺失或容量缺失。假定预取过程可以相互重叠，并能与缓存缺失重叠。因此可以用最高存储器带宽传输。下面是忽略缓存缺失的关键循环次数：原循环每次迭代需要7个时钟周期，第一次预取循环每次迭代需要9个时钟周期，第二次预取循环每次迭代需要8个周期（包含循环外部的开销）。一次缺失需要100个时钟周期。

（1）

• 直接映像Cache的容量大于数组a和b容量之和，因此只会发生强制不命中（失效）。
• a的元素按存储顺序读入，受益于空间局部性，一次读入一个块中含有2个数组元素，因此读入a时，j的偶数值缺失，奇数值命中。所以对a的访问会造成3×(100/2)=150次失效。
• b的元素受益于时间局部性，每次迭代的b[j][0]与上次迭代的b[j+1][0]相同，因此，每当第一次访问b[j][0]时，出现一次缺失，总计101次。

（2）

for （ j = 0;  j < 100;  j = j+1 ）  {
          prefetch （ b[ j+7 ][ 0 ]）;      
         /* 预取7次循环后所需的b （ j , 0 ） */
          prefetch （ a[ 0 ][ j+7 ]）;       
         /* 预取7次循环后所需的a （0 , j ） */
          a [0][ j ] = b[ j ][ 0 ] * b[ j+1 ][ 0 ]; 
}
for （ i = 1;  i < 3;  i = i+1 ）  
	for （ j = 0;  j < 100;  j = j+1 ）{
           prefetch （ a [ i ][ j+7 ]）;    
          /* 预取7次循环后所需的a （ i , j ） */
          a [ i ][ j ] = b[ j ][ 0 ] * b[ j+1 ][ 0 ];
   } /* a失效 7/2 = 4, 两次循环共失效8次 */

（3）
预取a[i][7]至a[i][99]，共93×3=279条。
预取b[7][0]至b[100][0]，共94条。
将非预取缺失的数目减至：

• 第一次循环中访问元素b[0][0]~b[6][0]的7次缺失。
• 第一，二次循环中访问a[i][0]到a[i][6]的3×（[7/2]）=12次缺失。（空间局部性）

总共避免了150+101-7-12=232次失效。
（4）
原来的双层嵌套循环执行3x100=300次。由于该循环每次迭代需要7个时钟周期，所以总共为300 × 7= 2100时钟周期再加上缓存缺失。缓存缺失增加 251 x 100=25 100个时钟周期，总共27 200个时钟周期。第一次预取循环迭代 100次，每次迭代为9个时钟周期，所以总共900个时钟周期再加上缓存缺失。现在加上缓存缺失的11x 100-1100个时钟周期，总共2000个时钟周期。第二个循环执行2x100=200次，每次迭代为8个时钟周期，所以需要 1600个时钟周期，再加上缓存缺失8x 100=800个时钟周期。总共2400个时钟周期。由上个例子可以知道，这一代码为了执行这两个循环，在 2000+2400=4400个时钟周期内执行了 400条预取指令。如果我们假定这些预取操作完全与其他执行过程相重叠，那么这一预取代码要快27200/4400=6.2倍。

7. 假定有一个计算机，当所有存储器访问都在缓存中命中时，其每条指令的周期数（CPI）为1.0。仅有的数据访问就是载入和存储，占总指令数的50%。如果缺失代价为25个时钟周期，缺失率为2%，当所有指令都在缓存中命中时，计算机可以加快多少？

“仅有的数据访问就是载入和存储，占总指令数的50%。”这句话等价于“每条指令平均访存1.5次”。
所有指令都在缓存中命中时，存储器停顿周期数为0。
$$\begin{array}{rl}CPU时{间}_{理想}& =IC\times CPI\times 时钟周期时间\\ & =1.0\times IC\times 时钟周期时间\end{array}$$
考虑缺失的情况下：
$$\begin{array}{rl}CPU时{间}_{有缺失}& =IC\times (CP{I}_{execution}+每条指令的平均访存次数\times 不命中率\times 不命中开销)\times 时钟周期时间\\ & =IC\times (1+1.5\times 2\%\times 25)\times 时钟周期时间\\ & =1.75\times IC\times 时钟周期时间\end{array}$$
性能是执行时间的倒数：
$$\frac{性{能}_{理想}}{性{能}_{有缺失}}=\frac{CPU时{间}_{有缺失}}{CPU时{间}_{理想}}=\frac{1.75\times IC\times 时钟周期时间}{1.0\times IC\times 时钟周期时间}=1.75$$
因此，当所有指令都在缓存中命中时，计算机可以加快1.75倍。

8. 假设对指令Cache的访问占全部访问的75%；而对数据Cache的访问占全部访问的25%。Cache的命中时间为1个时钟周期，失效开销为50 个时钟周期，在混合Cache中一次load或store操作访问Cache的命中时间都要增加一个时钟周期，32KB的指令Cache的失效率为0.39%，32KB的数据Cache的失效率为4.82%，64KB的混合Cache的失效率为1.35%。又假设采用写直达策略，且有一个写缓冲器，并且忽略写缓冲器引起的等待。试问指令Cache和数据Cache容量均为32KB的分离Cache和容量为64KB的混合Cache相比，哪种Cache的失效率更低？两种情况下平均访存时间各是多少？

$$分离Cache失效率=0.39\%\times 75\%+4.82\%\times 25\%=1.50\%$$
容量64KB的混合Cache失效率较低，只有1.35%。
$$\begin{array}{rl}平均访存时{间}_{分离Cache}& =1+75\%\times 0.39\%\times 50+25\%\times 4.82\%\times 50=1.75\\ 平均访存时{间}_{混合Cache}& =1+75\%\times 1.35\%\times 50+25\%\times (1+1.35\%\times 50)=1.925\end{array}$$

9. 给定以下的假设，试计算直接映象Cache和两路组相联Cache的平均访问时间以及CPU的性能。由计算结果能得出什么结论？
   （1）理想Cache情况下的CPI为2.0，时钟周期为2ns，平均每条指令访存1.2次；
   （2）两者Cache容量均为64KB，块大小都是32字节；
   （3）组相联Cache中的多路选择器使CPU的时钟周期增加了10％；
   （4）这两种Cache的失效开销都是80ns；
   （5）命中时间为1个时钟周期；
   （6）64KB直接映象Cache的失效率为1.4％，64KB两路组相联Cache的失效率为1.0％。

$$\begin{array}{rl}平均访问时{间}_{直接映射}& =2+1.4\%\times 80=3.12ns\\ 平均访问时{间}_{2路组相联}& =2.2+1.0\%\times 80=3.0ns\end{array}$$
$$\begin{array}{rl}CPU时{间}_{直接映射}& =IC\times (2+1.2\times 1.4\%\times \frac{80}{2})\times 2=5.344IC\\ CPU时{间}_{2路组相联}& =IC\times (2+1.2\times 1.0\%\times \frac{80}{2.2})\times 2.2=5.36IC\\ \frac{性{能}_{直接映射}}{性{能}_{2路组相联}}& =\frac{CPU时{间}_{2路组相联}}{CPU时{间}_{直接映射}}=\frac{5.36IC}{5.344IC}=1.003\end{array}$$
因此，2路组相联的平均访问时间较短，但是直接映射Cache的CPU性能较高。

10. 在伪相联中，假设在直接映象位置没有发现匹配，而在另一个位置才找到数据（伪命中）时，不对这两个位置的数据进行交换。这时只需要1个额外的周期。假设失效开销为50个时钟周期，2KB直接映象Cache的失效率为9.8%，2路组相联的失效率为7.6%；128KB直接映象Cache的失效率为1.0%，2路组相联的失效率为0.7%。
    （1）推导出平均访存时间的公式。
    （2）利用（1）中得到的公式，对于2KBCache和128KBCache，计算伪相联的平均访存时间。

（1）
$$\begin{array}{rl}平均访存时{间}_{伪相联}& =命中时{间}_{伪相联}+失效{率}_{伪相联}\times 失效开{销}_{伪相联}\\ 失效{率}_{伪相联}& =失效{率}_{2路}\\ 失效开{销}_{伪相联}& =失效开{销}_{1路}\\ 伪命中率& =命中{率}_{2路}-命中{率}_{1路}\\ & =(1-失效{率}_{2路})-(1-失效{率}_{1路})\\ & =失效{率}_{1路}-失效{率}_{2路}\end{array}$$
因此，$$平均访存时{间}_{伪相联}=命中时{间}_{1路}+(失效{率}_{1路}-失效{率}_{2路})\times 1+失效{率}_{2路}\times 失效开{销}_{1路}$$
（2）
$$\begin{array}{r}平均访存时{间}_{伪相联，2KB}=1+(9.8\%-7.6\%)+7.6\%\times 50=4.822\\ 平均访存时{间}_{伪相联，128KB}=1+(1.0\%-0.7\%)+0.7\%\times 50=1.353\end{array}$$