R语言实例：基于Boston数据集的数据分析报告——用 logistic 回归、LDA（线性判别法）、K 临近法（k=1 和 k=5）构建分类模型。目的是预测一个区域的犯罪率是否高于所有犯罪率的中位数

问题

请分析 Boston 数据集，并撰写一个数据分析报告。

在报告中主要分析并回答以下两个问题。

• 用 logistic 回归、LDA（线性判别法）、K 临近法（k=1 和 k=5）构建分类模型。目的是预测一个区域的犯罪率是否高于所有犯罪率的中位数。

  在构建每种类型的模型时，请分别选择三组（三个不同子集的）自变量。从三组自变量构造的模型中分别选出一个你认为最好的，你的选择应当基于交叉验证法。请讨论你得到的结果。

• 用最优子集的方法构建回归模型，预测一个区域的犯罪率。

Boston 数据集

查看数据集

> library(MASS)
> head(Boston) # 查看数据前6行
     crim zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat medv
1 0.00632 18  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98 24.0
2 0.02731  0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14 21.6
3 0.02729  0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03 34.7
4 0.03237  0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94 33.4
5 0.06905  0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33 36.2
6 0.02985  0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21 28.7

数据描述

在命令行中输入?Boston命令，Rstudio 界面出现该数据集的解释界面，如图所示：

Boston数据集描述波士顿郊区的房价，该数据集共506行、14列。

变量	含义
crim	城镇人均犯罪率
zn	25000平方英尺以上地块的住宅用地比例
indus	每个城镇的非零售业务面积比例
chas	Charles River 哑变量1（如果道沿河而行，该项数值为 1，否则为0）
nox	氮氧化物浓度(千万分之一)
rm	每个住宅的平均房间数
age	1940年以前建造的自有住房比例
dis	五个波士顿就业中心距离的加权平均数
rad	辐射状公路通达性指数
tax	按每10,000美元计算的全值物业税税率
ptratio	城镇师生比例
black	$1000(Bk-0.63{)}^2$，其中$Bk$是城镇黑人的比例
lstat	底层阶级人口占比（%）
medv	业主自住住宅的中位价值（以1000美元为单位）

构建分类模型

数据可视化

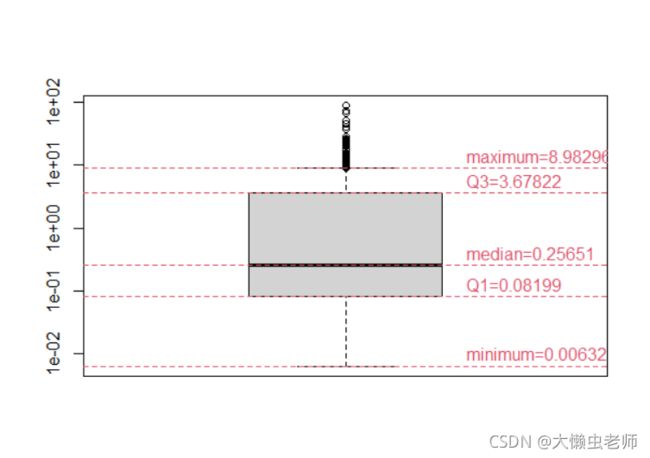
通过查看数据描述，我们知道了每个变量的含义。通过数据可视化，我们可以快速知道数据分布情况，便于下一步构造模型。查看 crim 变量，绘制箱线图。因为数值多分布在0-1范围内，所以在该箱线图中，对y轴的显示取对数，便于更方便地观察数据。

boxplot <- boxplot(Boston$crim,outline = T,log= "y")
boxplot$stats
abline(h=boxplot$stats[1,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[1,], "minimum=0.00632", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[2,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[2,], "Q1=0.08199", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[3,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[3,], "median=0.25651", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[4,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[4,], "Q3=3.67822", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[5,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[5,], "maximum=8.98296", col = 2,adj=c(0,-0.4))

logistic 分类模型

构建分类模型的因变量

构建 logistic 分类模型的因变量，该因变量是二分类的。我们将高于犯罪率（crim）中位数的项记为“1”，否则为“0”。

dt <- Boston# 将 Boston 赋值给 dt
# 构建新变量 crim_bi
# crim_bi：高于 crim 中位数的项记为“1”, 否则为“0”
dt$crim_bi <- ifelse(dt$crim > median(dt$crim), 1, 0)

构建三个不同自变量的模型

#### 构建3个模型 ####
log.fit <- glm(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
               data = dt , family = "binomial")
summary(log.fit)
log.fit2 <- glm(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
               data = dt , family = "binomial")
summary(log.fit2)
log.fit3 <- glm(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
                data = dt , family = "binomial")
summary(log.fit3)

交叉验证

进行交叉验证，将准确率作为衡量标准。

fold_log <- function(log.fit,dt){
  library(caret)
  set.seed(3)
  folds <- createFolds(y=dt[,10],k=10)
  accuracy <- as.numeric()
  for (i in 1:10){
    fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
    fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
    fold_pre<- predict(log.fit,fold_test,type = "response")
    log.class <- ifelse(fold_pre > 0.5, 1, 0)
    a <- table(log.class, fold_test$crim_bi)
    accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
  }
  return(mean(accuracy))
}

fold_log(log.fit,dt)
fold_log(log.fit2,dt)
fold_log(log.fit3,dt)

结果分析

> fold_log(log.fit,dt)
[1] 0.9150087
> fold_log(log.fit2,dt)
[1] 0.9229287
> fold_log(log.fit3,dt)
[1] 0.9090433

由输出结果可知，log.fit2 即第二个模型的准确率更高，为$0.9229287$。

LDA 回归模型

同理，

lda <- lda(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
           data = dt) 
lda2 <- lda(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
           data = dt) 
lda3 <- lda(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
           data = dt) 
fold_lda <- function(lda,dt){
  library(caret)
  set.seed(3)
  folds <- createFolds(y=dt[,10],k=10)
  accuracy <- as.numeric()
  for (i in 1:10){
    fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
    fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
    fold_pre<- predict(lda,fold_test)
    a <- table(predict(lda,fold_test)$class, fold_test$crim_bi)
    accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
  }
  return(mean(accuracy))
}
fold_lda(lda,dt)
fold_lda(lda2,dt)
fold_lda(lda3,dt)

结果分析

> fold_lda(lda,dt)
[1] 0.8556253
> fold_lda(lda2,dt)
[1] 0.8575861
> fold_lda(lda3,dt)
[1] 0.8635469

由输出结果可知，lda3 即第三个模型的准确率更高，为$0.8635469$。

K 临近模型

#### 模型1 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

#### 模型2 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

#### 模型3 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

最优子集构建回归模型

最优子集

library(leaps)
leaps<- regsubsets(crim ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
           data=dt)
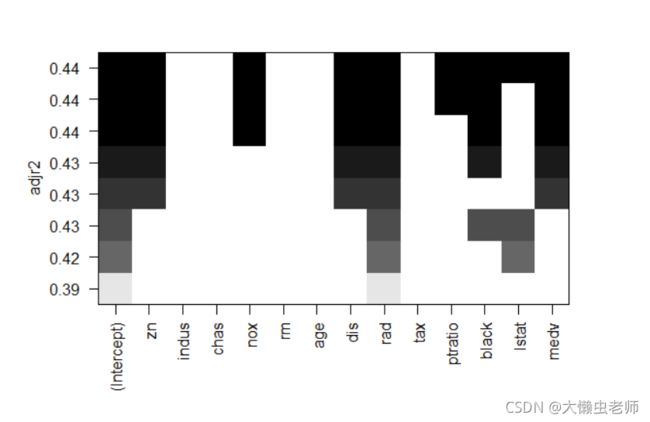
plot(leaps,scale = "adjr2")

如图所示，截距+rad的调整R平方值为$0.39$。调整R平方值越高的模型越好，因此最佳预测变量为：
zn+nox+dis+rad+ptratio+black+lstat+medv。

故有：

lmfit<- lm(crim ~ zn+nox+dis+rad+ptratio+black+lstat+medv,
                   data=dt)

划分学习和测试数据集

随机抽取$70\%$的数据放入学习数据集，剩余$30\%$放入测试数据集。

dim(dt)
length <- dim(dt)[1]
set.seed(1)
pre <- sample(length,length*0.7)# 随机抽取70 %的观测放入学习数据集
pre <- sort(pre)
train <- dt[pre,]# 学习数据集train
test <-  dt[-pre,]# 剩余30 %放入测试数据集test

预测犯罪率

写一个计算均方误差的函数RMSE:

RMSE=function(t,p){
  return(sqrt(mean((t-p)^2)))
}

用测试数据集预测犯罪率，并计算均方误差：

lm_pre<- predict(lmfit, test) 
RMSE(test$crim,lm_pre)

计算知：

> RMSE(test$crim,lm_pre)
[1] 7.557481

则均方误差为$7.557481$。

代码

rm(list=ls())# 把当前环境中的对象全部删除
library(ggplot2)
library(dplyr)
library(MASS)
head(Boston)# 查看数据前6行
#### 箱线图 ####
boxplot <- boxplot(Boston$crim,outline = T,log= "y")
boxplot$stats
abline(h=boxplot$stats[1,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[1,], "minimum=0.00632", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[2,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[2,], "Q1=0.08199", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[3,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[3,], "median=0.25651", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[4,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[4,], "Q3=3.67822", col = 2,adj=c(0,-0.4))

abline(h=boxplot$stats[5,],lwd=1,col=2,asp = 2,lty = 2)
text(1.25,boxplot$stats[5,], "maximum=8.98296", col = 2,adj=c(0,-0.4))

#### logistic 回归模型 ####
dt <- Boston# 将 Boston 赋值给 dt
# 构建新变量 crim_bi
# crim_bi：高于 crim 中位数的项记为“1”, 否则为“0”
dt$crim_bi <- ifelse(dt$crim > median(dt$crim), 1, 0)

#### 构建3个模型 ####
log.fit <- glm(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
               data = dt , family = "binomial")
summary(log.fit)
log.fit2 <- glm(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
               data = dt , family = "binomial")
summary(log.fit2)
log.fit3 <- glm(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
                data = dt , family = "binomial")
summary(log.fit3)


fold_log <- function(log.fit,dt){
  library(caret)
  set.seed(3)
  folds <- createFolds(y=dt[,10],k=10)
  accuracy <- as.numeric()
  for (i in 1:10){
    fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
    fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
    fold_pre<- predict(log.fit,fold_test,type = "response")
    log.class <- ifelse(fold_pre > 0.5, 1, 0)
    a <- table(log.class, fold_test$crim_bi)
    accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
  }
  return(mean(accuracy))
}

fold_log(log.fit,dt)
fold_log(log.fit2,dt)
fold_log(log.fit3,dt)

#### 划分测试和学习数据集 ####
dim(dt)
length <- dim(dt)[1]
set.seed(5)
pre <- sample(length,length*0.8)#随机抽取 80%的观测放入学习数据集
pre <- sort(pre)# 排序
train <- dt[pre,]# 随机抽取 80%的观测放入学习数据集train
test <-  dt[-pre,]# 测试数据集test

log.pred <- predict(log.fit2, test, type = "response")
log.class <- ifelse(log.pred > 0.5, 1, 0)
# 混淆矩阵
table(log.class, test$crim_bi)

#### LDA 回归模型 ####
lda <- lda(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
           data = dt) 
lda2 <- lda(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
           data = dt) 
lda3 <- lda(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
           data = dt) 
fold_lda <- function(lda,dt){
  library(caret)
  set.seed(3)
  folds <- createFolds(y=dt[,10],k=10)
  accuracy <- as.numeric()
  for (i in 1:10){
    fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
    fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
    fold_pre<- predict(lda,fold_test)
    a <- table(predict(lda,fold_test)$class, fold_test$crim_bi)
    accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
  }
  return(mean(accuracy))
}
fold_lda(lda,dt)
fold_lda(lda2,dt)
fold_lda(lda3,dt)
#### K 临近模型 ####
#### 模型1 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

#### 模型2 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+indus+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

#### 模型3 ####
# k=1
library(kknn)
library(caret)
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=1)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)
# k=5
set.seed(3)
folds <- createFolds(y=dt[,10],k=10)
accuracy <- as.numeric()
for (i in 1:10){
  fold_test <- dt[folds[[i]],] #取folds[[i]]作为测试集
  fold_train <- dt[-folds[[i]],] # 剩下的数据作为训练集
  knn <- kknn(crim_bi ~ zn+nox+age+dis+rad+tax+ptratio+black+medv,
              fold_train,fold_test,k=5)
  pre_knn <- fitted(knn)
  pre_knn <- ifelse(pre_knn > 0.5, 1, 0)
  a <- table(pre_knn, fold_test$crim_bi)
  accuracy <- append(accuracy,(a[1]+a[4])/sum(a))
}
mean(accuracy)

library(leaps)
leaps<- regsubsets(crim ~ zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat+medv,
           data=dt)
plot(leaps,scale = "adjr2")
lmfit<- lm(crim ~ zn+nox+dis+rad+ptratio+black+lstat+medv,
                   data=dt)

dim(dt)
length <- dim(dt)[1]
set.seed(1)
pre <- sample(length,length*0.7)# 随机抽取70 %的观测放入学习数据集
pre <- sort(pre)
train <- dt[pre,]# 学习数据集train
test <-  dt[-pre,]# 剩余30 %放入测试数据集test

lm_pre<- predict(lmfit, test) 
RMSE=function(t,p){
  return(sqrt(mean((t-p)^2)))
}
RMSE(test$crim,lm_pre)

---

1. 哑变量一般指虚拟变量。 虚拟变量 ( Dummy Variables) 又称虚设变量、名义变量或哑变量，用以反映质的属性的一个人工变量，是量化了的自变量，通常取值为0或1。引入哑变量可使线形回归模型变得更复杂，但对问题描述更简明。 ↩︎