卷积函数代码实现运算

卷积核通常是单数：1、3、5、7、9

#先产生一些变量，这些变量是常数，用1.0表示，5*5个数据，tensorflow只能表示四维数据，不够就补0
input1=tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 1])) #(b, h, w, c)

b：处理的批次
c：输入数据经过处理后输出的特征数量（通道数量）

通道数越多，特征越丰富

卷积的过程就是处理滑动窗口的过程，即对原始特征进行提取的过程

几个卷积核，就是几个通道，就是几个特征

卷积核（filter）：[h, w, i ,c]
h：高
w：宽
i：卷积核的输入通道数（=输入数据的输出通道）
c：卷积之后输出几个通道

原始的输入数据（imput）输出几个通道，卷积核就输入几个通道：

h表示2行，w表示2列
filter有几个通道（c）就几个一组，这里是1个

卷积核输出的一个通道：

[[[[-1]], [[ 0]]],    [-1  0
 [[[ 0]], [[-1]]]]      0 -1]
'''
filter1=tf.Variable(tf.constant([-1.0, 0, 0, -1.0], shape=[2, 2, 1, 1]))

按照如下步骤将卷积核写成能够表示的形式：
①c=2，两个数一组：
[-1，0]，[0，-1]，
[-1，0]，[0，-1]
②所有数最外面一维：
[[-1，0]，[0，-1]，
[-1，0]，[0，-1]]
③每行一维：
[[[-1，0]，[0，-1]]，
[[-1，0]，[0，-1]]]
④逗号间隔一维度：
[[[[-1，0]]，[[0，-1]]]，
[[[-1，0]]，[[0，-1]]]]
能够表示的形式：
[[[[-1，0]]，[[0，-1]]]，
[[[-1，0]]，[[0，-1]]]]

从外往里数维数，最外面的"[ ]"是1维

根据可表示的形式写出可运算的形式：
[-1，0， [0，-1
-1，0] 0，-1]
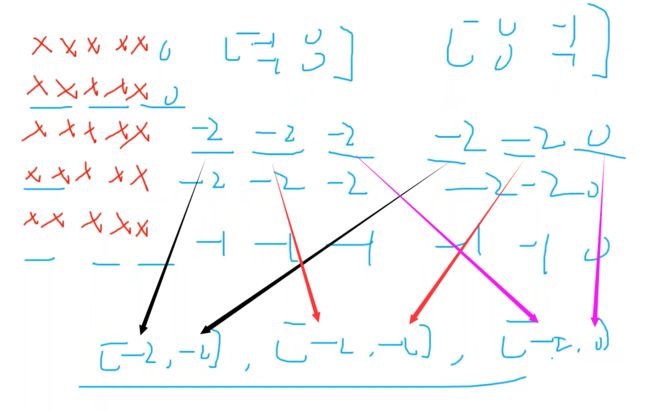
方法见下图：同颜色圈出的放一起
（左边是可显示的，右边是可参与运算的）

有几个通道就几个一组，这个是两个通道：

两个通道：

'''
filter:h=2, w=2, i=1, c=2. 
[[[[-1, 0]], [[0, -1]]],               [-1, 0,      [0, -1
 [[[-1, 0]], [[0, -1]]]                 -1, 0]       0, -1]
'''
filter2=tf.Variable(tf.constant([-1.0, 0, 0, -1.0, -1.0, 0, 0, -1.0], 
                                shape=[2, 2, 1, 2]))

后面的同理：

'''
filter:h=2, w=2, i=1, c=3. 
[[[[-1,  0,  0]], [[-1, -1,  0]]],                 [-1, -1,      [ 0, -1,      [ 0,  0
 [[[ 0, -1, -1]], [[ 0,  0, -1]]]                    0,  0]       -1,  0]       -1, -1]
'''
filter3=tf.Variable(tf.constant([-1.0, 0, 0, -1.0, -1.0, 0, 0, -1.0, 
                                 -1.0, 0, 0, -1.0], shape=[2, 2, 1, 3]))

'''
filter:h=2, w=2, i=2, c=2. 
[[[[-1, 0], [0, -1]], [[-1, 0], [0, -1]]],               [-1, 0 +[ 0, -1       [-1, 0 +[ 0, -1 
 [[[-1, 0], [0, -1]], [[-1, 0], [0, -1]]]                 -1, 0]+  0, -1]       -1, 0]+  0, -1]
'''
filter4=tf.Variable(tf.constant([-1.0, 0, 0, -1.0, -1.0, 0, 0, -1.0, 
                                 -1.0, 0, 0, -1.0, -1.0, 0, 0, -1.0], 
                                shape=[2, 2, 2, 2]))

'''
filter:h=2, w=2, i=2, c=1. 
[[[[-1], [0]], [[0], [-1]]],            [-1, 0       [0, -1
 [[[-1], [0]], [[0], [-1]]]]             -1, 0]       0, -1]
'''
filter5=tf.Variable(tf.constant([-1.0, 0, 0, -1.0, -1.0, 0, 0, -1.0], 
                                shape=[2, 2, 2, 1]))

---

卷积公式：
valid（不能补0）：越卷越小
same（能补0）：卷完大小不变

VALID:out=(in-filter+1)ride 上取整
SAME:out=inride 上取整
#补0规则：
P=(out-1)*stride+filter-in
P_L=P_U=P/2
P_R=P_D=P-P_L

op1=tf.nn.conv2d(input1, filter1, strides=[1, 2, 2, 1], padding='SAME')#输入数据，卷积核，步长（每次取两个），补0规则是SAME
op1=tf.nn.conv2d(input1, filter1, strides=[1, 2, 2, 1], padding='SAME')
op2=tf.nn.conv2d(input1, filter2, strides=[1, 2, 2, 1], padding='SAME')
op3=tf.nn.conv2d(input1, filter3, strides=[1, 2, 2, 1], padding='SAME')
op4=tf.nn.conv2d(input2, filter4, strides=[1, 2, 2, 1], padding='SAME')
op5=tf.nn.conv2d(input2, filter5, strides=[1, 2, 2, 1], padding='SAME')
vop1=tf.nn.conv2d(input1, filter1, strides=[1, 2, 2, 1], padding='VALID')
op6=tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding='SAME')
vop2=tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding='VALID')

strides在官方定义中是一个一维具有四个元素的张量，其规定前后必须为1，所以可以改的是中间两个数，中间两个数分别代表了水平滑动和垂直滑动步长值

init=tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    print('op1:\n', sess.run([op1, filter1]))
    print('='*20)

op1：
手算结果：

运行结果：

后面的同理：

init=tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    print('op1:\n', sess.run([op1, filter1]))
    print('='*20)
    print('op2:\n', sess.run([op2, filter2]))
    print('='*20)
    print('op3:\n', sess.run([op3, filter3]))
    print('='*20)
    print('op4:\n', sess.run([op4, filter4]))
    print('='*20)
    print('op5:\n', sess.run([op5, filter5]))
    print('='*20)
    print('vop1:\n', sess.run([vop1, filter1]))
    print('='*20)
    print('op6:\n', sess.run([op6, filter1]))
    print('='*20)
    print('vop2:\n', sess.run([vop2, filter1]))
    print('='*20)

op2：补0，相乘，得结果

op3：补0，相乘，得结果

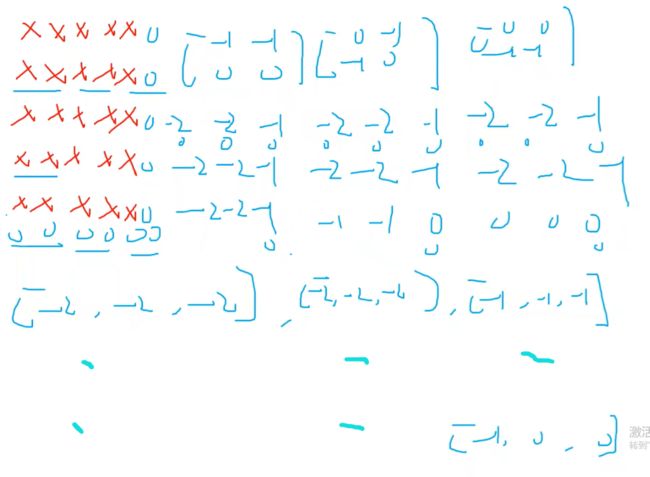
op4：分别相加得出两个矩阵

再两个一组取出来

op5：和op4类似，但是中间不相加了，直接合并

vop1:valid不补0

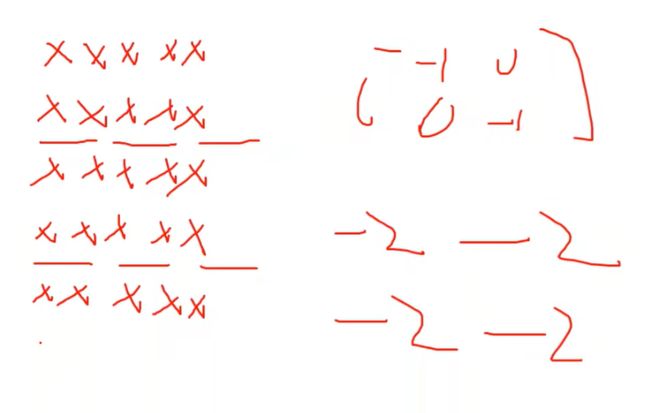
op6和vop2和上面的类似

运行结果：