matlab 拉普拉斯锐化函数_DIP第三章图像增强高斯拉普拉斯算子零交叉点

Welcome​zqsiat.github.io

写在前面的

老师在布置这道作业题的时候说“这次作业非常简单，比上次第二章的作业简单，不会花太长时间就可以完成。”当时我还真信了，但是，并不简单。吐槽一下，我们老师讲课对我们学生的水平太过自信，有些细节的东西不讲，其中滋味请大家自行脑补。

作业内容

鉴于LoG算法在历史中的地位，进行较深入的实验研究探讨不同σ对LoG 算法的影响。图像Chapter3_1.pgm计算公式（*表卷积）见(1) 式

（1）

取σ =1.2然后求零交叉的结果；取σ =2.8的然后求零交叉的结果；讨论和结论：零交叉对σ的依赖性。

注意：卷积模板大小取正方形NxN，N不小于3σ，卷积模板由(2)式确定

补充：零交叉结果 - 生成二值图像，零交叉用1表示（显示为255）、其他的用0表示（显示为0）。

（2）

图1、Chapter3_1.pgm

图像增强

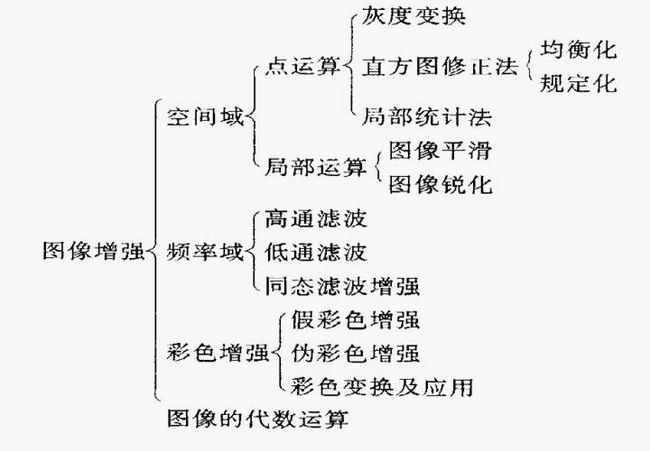
老师的PPT内容很少，所以我找到了国科大校区的课件，用以补充相关知识。首先图像增强的分类，盗一张大图大家看一下，因为之前老师没讲这个，看到它时，感觉自己发现了新大陆：

图2、图像增强分类

这次作业内容属于图像锐化，图像锐化和图像平滑都是空间域滤波。空域滤波原理：建立模板，并在待处理的图像中逐点移动模板，对每个像素点按照滤波器算法进行计算。微分滤波器是图像锐化的一种滤波器。微分滤波器的原理，均值产生平滑的效果，而均值与积分相似，由此而联想到，微分则能产生相反的效果。

高斯拉普拉斯

首先这坨公式它是怎么来的呢？

LoG算子：

其中标准高斯函数，G(x,y)标准差δ ：

对一个标准高斯函数（未归一化）进行二次偏微分：

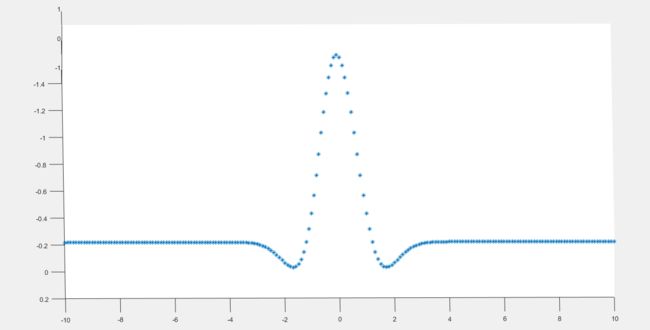
最终表达式：

LoG零交叉出现在

处LoG函数剖面图，沿着直径切开，如下图，看其形状，故而也被叫做墨西哥草帽算子。

图3、LoG函数刨面图

卷积模板

那这个卷积模板应该怎么求呢？它具有哪些性质呢？首先看一下应该怎么代入（x, y）的值求取卷积模板，这个很费劲，网上都是一些现成的模板，没有找到相关的怎么求取卷积模板的代码或者说明文字，最后我综合了一位大神的代码和matlab官方的卷积模板函数，该方法在matlab->edge()->fspecial()里，下面将这块代码贴出：

% Laplacian of Gaussian
     

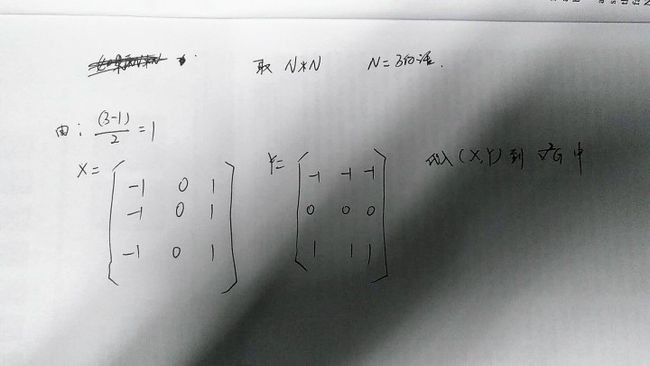
如果需要求取的模板大小为N*N=9时，需要带入的（x, y）如下：

图4、卷积模板代入值

需要注意是，N一般取奇数，然后正负(N-1)/2就是x的取值范围，步进间隔默认是1。

求得的卷积模板应该具有以下性质：

1. 该模板对平坦区域应该无响应，所以算子内系数和应该为0，使用公式计算出来的结果不为零，需要整体上下平移模板；
2. LoG可以使用laplace算子和高斯模板进行卷积后求得，其等效于使用LoG大小和标准差的高斯平滑后得到laplace结果；
3. 得到的结果要检测零交叉来定位边缘，因为噪声等原因，这里进行判断时可以使用阈值，也就是当出现零交叉的时候还要判断下正负值的差的绝对值是否满足阈值要求。；
4. LoG模板的大小和标准差的选择关系，遵循高斯分布的3δ原则，也就是当位置超过均值正负3δ以外的值很小，也就是说，LoG模板应该选择大于6δ的最小奇数作为模板大小，（PS：这条性质和老师作业所提的N应该大于或等于3δ的不同，为什么呢？？？）过大效果不会有提高反而增加计算量，过小会造成截断，无法得到正确结果。

卷积操作

卷积操作该怎么实现呢？这个操作有现成的函数可以调用，第一种方法就是使用openCV自带的filter2D()函数，一行代码搞定：之后经过询问老师后，使用该函数不能得到正确的结果。

filter2D

但是它好像默认输出图像的像素值为uchar类型的数据，为了后面的求取零交叉点做准备，就有了第二种方法，自己写一个卷积操作函数，并将像素值保存为double类型。按照《数字图像处理》第91页卷积过程，我编写了卷积操作，代码如下：

for 

访问Mat类图像我采用了傻瓜的方式dst.at(x, y)。大致过程是这样的，首先新建一个临时图像，在原图得基础上将图像得长和宽分别增加2*(N-1)个像素点，并将原图拷贝到临时图像中心，然后进行图像遍历。遍历之后再从结果中截取原图大小得卷积之后得图像，就得到了最后得结果。

求取零交叉点（经过老师的讲解和栋哥的指导，终于懂了求取零交叉点的方法）

求取零交叉点并不是简单的对图像进行二值化操作，二值化操作的的方法有很多，第一种，直接设置阈值的方法，和openCV官方的threshold()函数一样，在生成卷积结果时候直接加一行代码即可：坦白来说这种方法并不是求零交叉点的方法。

sumLaplacian 

第二种，既设置阈值又判断它的4邻域范围内是否有负的像素值，代码如下：这种方法无法得到正确的零交叉点，有可能零交叉点在两个相邻像素的亚像素点。

//3x3的邻域内，如果中心像素大于阈值，切周围存在负像素值，则此点为0交叉点

第三种，以p为中心的一个3*3领域，p点处的零交叉意味着至少有两个相对的领域像素的符号不同。在这个基础上还要判断中心点p的值介于两个符号不同像素的值之间，就是p的值要小于两个符号不同的像素的绝对值。如果是，那才可以判断为零交叉点。代码如下：

	//以P为中心的一个3*3领域，p点处的零交叉意味着至少有两个相对的领域像素的符号不同。
	//有四种要测试的情况：
        //P的值介于两个符号不同像素的值之间，就是P的值要小于两个符号不同的像素的绝对值。
	for (int y = 1; y < result.rows - 1; ++y)
	{
		for (int x = 1; x < result.cols - 1; ++x)
		{
			result.at(y, x) = 0;
			// 邻域判定  
			if (labs(dst.at(y, x)) < labs(dst.at(y - 1, x)) && 
				labs(dst.at(y, x)) < labs(dst.at(y + 1, x)) &&
				(dst.at(y - 1, x) * dst.at(y + 1, x)) <= 0)
			{
				result.at(y, x) = 255;
			}
			if (labs(dst.at(y, x)) < labs(dst.at(y , x - 1)) &&
				labs(dst.at(y, x)) < labs(dst.at(y , x + 1)) &&
				(dst.at(y , x- 1) * dst.at(y , x+ 1)) <= 0)
			{
				result.at(y, x) = 255;
			}
			if (labs(dst.at(y, x)) < labs(dst.at(y + 1, x - 1)) &&
				labs(dst.at(y, x)) < labs(dst.at(y - 1, x + 1)) &&
				(dst.at(y + 1, x - 1) * dst.at(y - 1, x + 1)) <= 0)
			{
				result.at(y, x) = 255;
			}
			if (labs(dst.at(y, x)) < labs(dst.at(y - 1, x - 1)) &&
				labs(dst.at(y, x)) < labs(dst.at(y + 1, x + 1)) &&
				(dst.at(y - 1, x - 1) * dst.at(y + 1, x + 1)) <= 0)
			{
				result.at(y, x) = 255;
			}			
		}
	}

结果分析

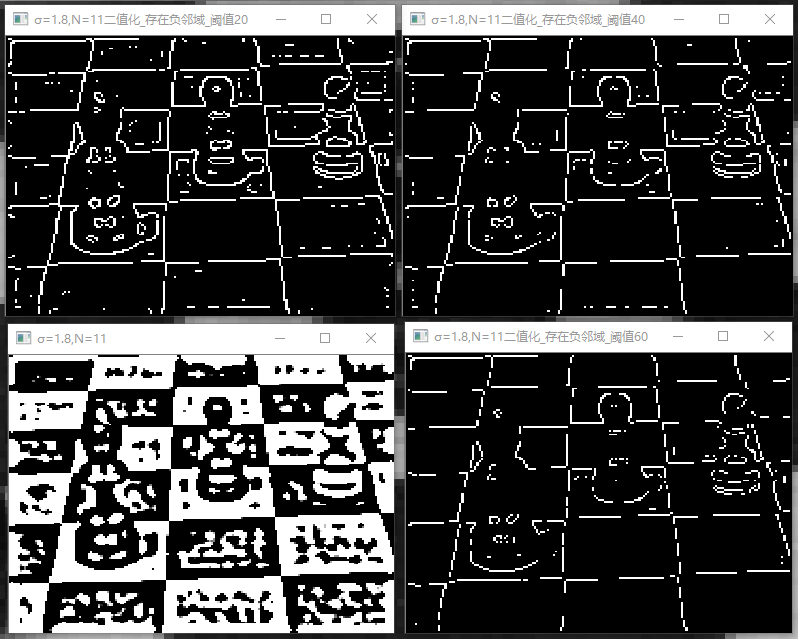
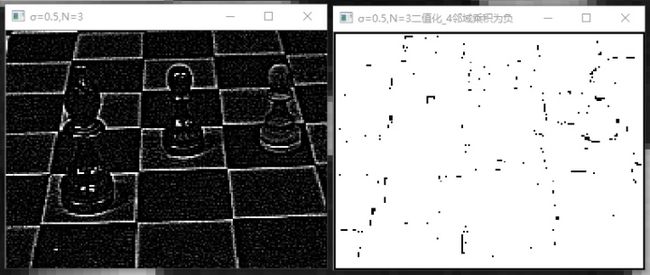
使用:“N3”、“N5”、“N9”、“N11”分别表示当σ=0.5、1.2、2.8、1.8，N=3、5、9、11的控制变量。“B”和"A"分别表示使用自己的卷积函数、filter2D函数这两组控制变量，“01”、“02”、“03”分别三种二值化方法的控制变量，对于“01”,“02”，阈值分别取20、40、60。在我的代码中重点对第三种方法进行了讨论，其实第一种方法和第二种方法求得的零交叉点都是不对的。第三种方法分为P的绝对值要小于两个符号不同的像素的绝对值和P点的绝对值是8邻域内的最小值进行对比，后发现后者是前者的子集。以上试验均使用VS2015和openCV2.7.14编译运行程序，运行结果如下：

图4-1、N3 A 01

图4-2、N5 A 01

图4-3、N9 A 01

图4-4、N11 A 01

图5-1、N3 B 01

图5-2、N5 B 01

图5-3、N9 B 01

图5-4、N11 B 01

图6-1、N3 A 02

图6-2、N5 A 02

图6-3、N9 A 02

图6-4、N11 A 02

图7-1、N3 B 02

图7-2、N5 B 02

图7-3、N9 B 02

图7-4、N11 B 02

图8-1、N3 A 03

图8-2、N5 A 03

图8-3、N9 A 03

图8-4、N11 A 03

图9-1、N3 B 03

图9-2、N5 B 03

图9-3、N9 B 03

图9-4、N11 B 03

通过分析图4-1、图4-2、图4-3、图4-4可以得出，当σ=1.2时，设置二值化阈值为60时的二值化效果最好，基本上没有任何噪点，且每一个十字边缘也很好的显示出来。随着σ的增加，卷积后的图像变得模糊，基本分不清十字交叉点，当σ很小时，又会出现噪点。通过分析图5-1、图5-2、图5-3基本可以得出一样的结论，但是对比卷积后的图像可以得出结论，openCV官方的filter2D函数可能自带滤波器，而且我写的卷积函数的出的图像在显示时可能通过处理，无法显示负值，或者将负值显示为0，所以看起来不如filter2D函数处理的好。

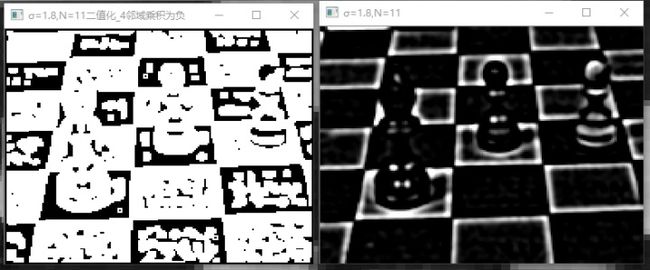
通过分析图5-1、图5-2、图5-3、图5-4、图6-1、图6-2、图6-3、图6-4可以得出，设置阈值，并判断4邻域是否存在负值的操作可以有效的滤除噪点，但是当σ增大时也会造成的十字边角的消失，但是对比只设置阈值的方法，他的模糊程度降低了不少，总之还是比单纯设置阈值的方法更好。

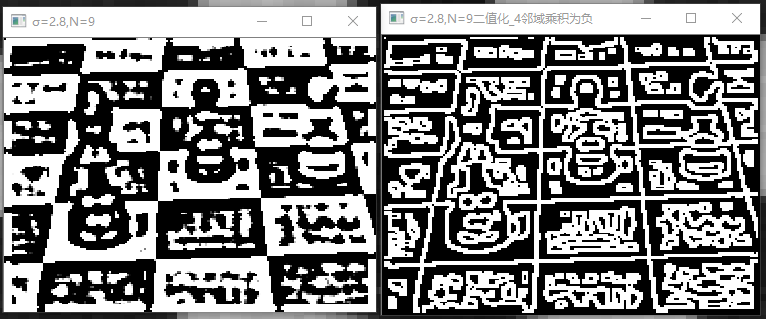
通过的分析图5-*、图6-*、图7-*、图8-*、图9-*可以得出，判断4邻域4组相对像素点的乘积是否存在负值，当σ=0.5，N = 3时，全是噪点，二值化后的图像基本无法分辨边角，当但逐渐增加σ的值后，当σ=1.2，N=5时二值化后的效果很明显，它可以最精确的还原图像的十字边角，当σ=1.2，N=11时，依然还原的很精确。

Welcome​zqsiat.github.io

附件：C++ ，openCV

//opencv版本:OpenCV2.7.13

PS：欢迎大家批评指正。