麦克风阵列声源定位四通道麦克风数据库及TDOA双曲交汇定位算法实验

麦克风阵列声源定位四通道麦克风数据库建立

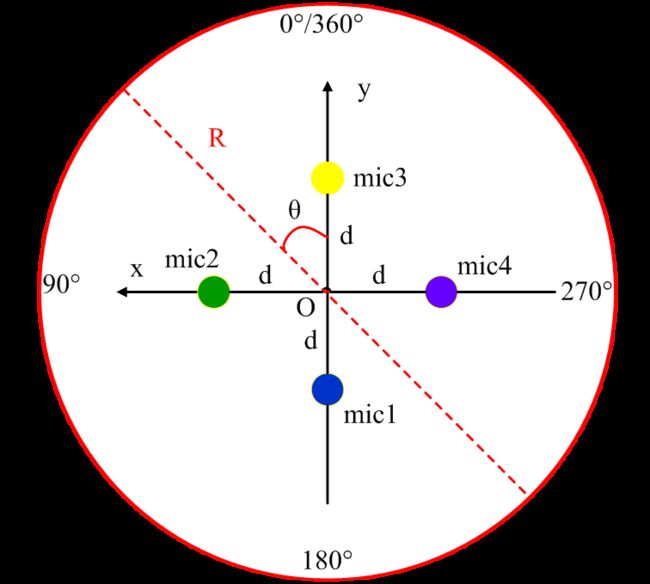
四通道麦克风数据库建立物理模型的建立，来源于文献：SLoClas: A DATABASE FOR JOINT SOUND LOCALIZATION AND CLASSIFICATION
根据图一，声源处于红色圆形上，且声源距离麦克风阵列中心O点的距离为1.5m,其中
mic1(0,-d)、mic2(d,0)、mic3(0,d)、mic4(-d,0) d为0.03m
声源会沿着红色圆圈按照θ角度旋转，麦克风阵列会依次按照一定的采样率每θ角度采集相同数据长度的声源数据，不同麦克风会因为距离角度而导致采集到的信号的幅度和相位不同。实验数据是按照θ=5°采集完成的，实验部分数据集如下图：

TDOA相关法时延求解

TDOA相关法时延求解原理与算法

双曲交汇定位算法

参考文献：运 用 双 曲 线 知 识 测 定 声 源
———研究性学习课题成果

结合图一，以mic2、mic4为焦点构建双曲线方程1：

以mic1、mic3为焦点构建双曲线方程2：

现在定义，T42为声源到mic4的时间与声源到mic2的时间的差，T13为声源到mic1的时间与声源到mic3的时间的差c为声音传播的速度，在这里c=340m/s。
根据双曲线的特性，其中，


两个双曲线方程联立求解，双曲线的交点就是声源的坐标。根据作者何晓东 郑东风 指导教师 支 静的文献，联立两个双曲线方程组求解得：

我们只需要根据T42和T13和0的关系来判定声源的具体位置即可，如下图所示：

声源位置、角度求解与算法代码验证

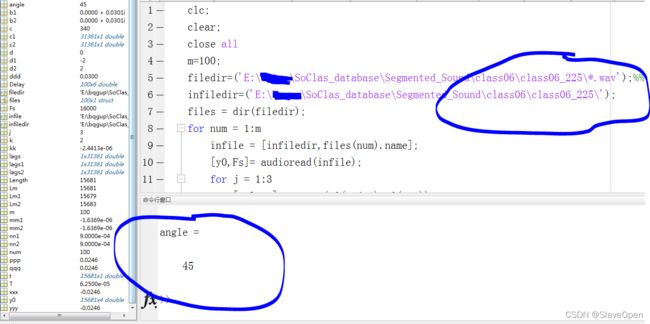
matlab的算法代码如下：

clc;
clear;
close all
m=100;
filedir=('E:\***\SoClas_database\Segmented_Sound\class06\class06_360\*.wav');%%
infiledir=('E:\***\SoClas_database\Segmented_Sound\class06\class06_360\');
files = dir(filedir);
for num = 1:m
    infile = [infiledir,files(num).name];
    [y0,Fs]= audioread(infile);
    for j = 1:3
        [c,lags] = xcorr(y0(:,j+1),y0(:,1));
        [Am,Lm] =  max(c);
        d = Lm - (length(c)+1)/2;
        Delay(num,j)=d/Fs;
    end
    for k = 1:2
        [c1,lags1] = xcorr(y0(:,k+2),y0(:,2));
        [Am1,Lm1] =  max(c1);
        d1 = Lm1 - (length(c1)+1)/2;
        Delay(num,k+3)=d1/Fs;   
    end
    [c2,lags2] = xcorr(y0(:,3),y0(:,4));
    [Am2,Lm2] =  max(c2);
    d2 = Lm2 - (length(c2)+1)/2;
    Delay(num,6)=d2/Fs;   
end

Length = length(y0);
T = 1 / Fs;
t = (1 : Length) * T;
t = t';
figure;
 subplot(411);
plot(t,y0(:,1));
title('mic1');
xlabel('（秒）')
ylabel('幅度（V）')
subplot(412);
plot(t,y0(:,2));
title('mic２');
xlabel('（秒）')
ylabel('幅度（V）')
subplot(413);
plot(t,y0(:,3));
title('mic３');
xlabel('（秒）')
ylabel('幅度（V）')
subplot(414);
plot(t,y0(:,4));
title('mic４');
xlabel('（秒）')
ylabel('幅度（V）')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
c = 340;
ddd = 0.03;
a1 = c*Delay(1,5);
b1 = sqrt(ddd*ddd - a1 * a1);
a2 = c*Delay(1,2);
b2 = sqrt(ddd*ddd - a2 * a2);
kk = b1*b1*b2*b2 - a1*a1*a2*a2;
mm1 = a1*a1*b2*b2;
mm2 = a2*a2*b1*b1;
nn1 = a2*a2+b1*b1;
nn2 = a1*a1+b2*b2;
ppp = sqrt(mm1*nn1/kk);
qqq = sqrt(mm2*nn2/kk);
if a2 > 0
    yyy = -qqq;
else
    yyy = qqq;
end 
if a1 > 0
    xxx = ppp;
else
    xxx = -ppp;
end
angle = atan(xxx / yyy)*180/pi
% if angle <= 0
%     theta = -angle + 180
% else
%     theta = angle
% end

上述代码可以通过c语言移植到具备算力的开发板中，根据数据集中的按照不同θ角度的麦克风阵列数据，分别进行角度验证，锁定声源的坐标，根据求得的角度在代入R即可求出声源的实际距离。测试结果如下：









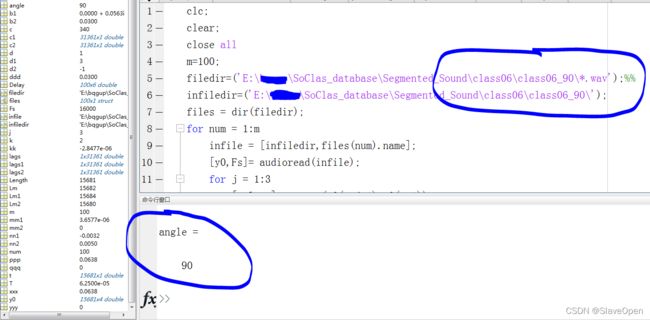
可以看出，双曲交汇定位算法是有一定效果的。良好的定位效果和声源距离麦克风阵列的距离、声源所发声信号的类型频率、背景噪声等有关，下一步将继续优化定位算法，使定位结果更加精准。

上述结构四通道麦克风定位数据集下载

链接：https://pan.baidu.com/s/1t63N73ZDFx9Ih6aeBISrRA
提取码：esnp

定位精度时延改进——时域预处理

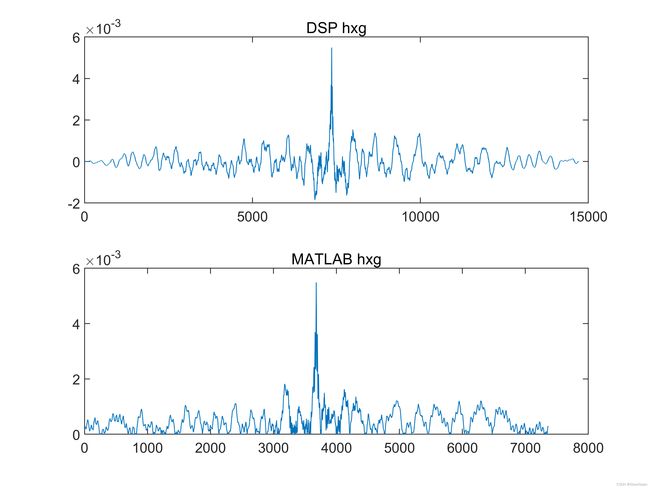
为了提高数据精度，需要对时域信号进行预处理——立方处理。就是对时域信号的每个点做三次幂处理。

未预处理实验

close all;
clear;
clc;
[time_txt,Fs] = audioread('E:\***\SoClas_database\Segmented_Sound\class06\class06_270\class06_270_001.wav');
LEN = 7361;
x1 = time_txt(:,1);
x2 = time_txt(:,2);
% xxx1 = x1.*x1.*x1;
% xxx2 = x2.*x2.*x2;
xxx1 = x1;
xxx2 = x2;
X1=(fft(xxx1));
X2=(fft(xxx2));
Sxy=X1.*conj(X2);
Bxy=fftshift(abs(ifft(Sxy)));
figure;
subplot(211);
Xxy=xcorr(xxx1,xxx2);
plot(Xxy);
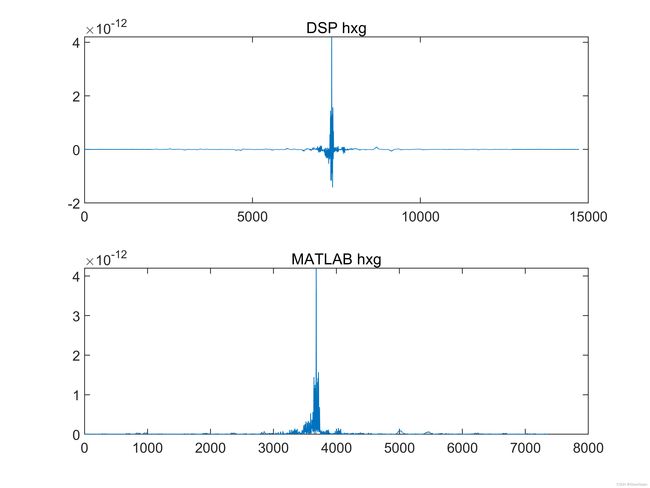
title('DSP hxg')
subplot(212);
plot((Bxy));
title('MATLAB hxg')

预处理实验

close all;
clear;
clc;
[time_txt,Fs] = audioread('E:\***\SoClas_database\Segmented_Sound\class06\class06_270\class06_270_001.wav');
LEN = 7361;
x1 = time_txt(:,1);
x2 = time_txt(:,2);
xxx1 = x1.*x1.*x1;
xxx2 = x2.*x2.*x2;
X1=(fft(xxx1));
X2=(fft(xxx2));
Sxy=X1.*conj(X2);
Bxy=fftshift(abs(ifft(Sxy)));
figure;
subplot(211);
Xxy=xcorr(xxx1,xxx2);
plot(Xxy);
title('DSP hxg')
subplot(212);
plot((Bxy));
title('MATLAB hxg')