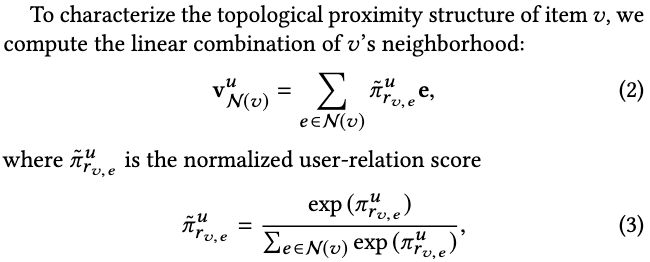KGCN:Knowledge Graph Convolutional Networks for Recommender Systems
emm…图片复制过来显示不了(因为我太懒了0.0),要看图的话可以去我的博客瞅瞅,嘿嘿嘿
对了,有些英文短句假如翻译成中文,阅读的时候就太搞脑子了,所以我干脆就不翻译了
我的博客地址:https://hikg.net/archives/119/
Introduction
Advantages of KG-based RS
将KG整合进推荐系统具有以下3种优点:
- KG中的item之间具有丰富的语义关联性,可以帮助探索它们之间的潜在联系,并且提高预测结果的准确性。
- KG中具有各种各样的关系,有助于合理地扩展 user的兴趣,并增加推荐item的多样性。
- KG连接了user的历史喜欢、推荐item,从而为RS引入了可解释性。
Challenges of KG-based RS
但是,由于KG具有高维度、异质性,在RS中应用KG十分具有挑战性。
一种可行的方法是,通过KGE方法对KG进行预处理,这种方法将实体、关系映射为低维度的表示向量。然而,常用的KGE方法侧重于对严格的语义相关性进行建模,它们更适合in-graph的应用(如KG completion、链接预测)
一种更自然、直观的方法是,设计一个graph算法,去直接探究KG的结构。
例如PER、FMG将KG视作一个异构信息网络,并且抽取出基于meta-path或meta-graph的潜在特征,来表示user、item(沿着不同关系类型的path或graph)之间的连通性。但是,PER、FMG严重依赖于人工设计的meta-path或meta-graph。
RippleNet
Key Idea of KGCN
设计目标:自动捕捉KG中的高阶结构、语义信息。
关键思想:在计算KG中的一个给定实体的表示时,将带有bias的邻域信息进行汇总、合并。
优点:
- 通过邻域的聚合操作,成功捕获到了局部邻近结构(local proximity structure),并将其存储在每个实体中
- 邻居的权重,取决于连接关系(connecting relation)、特定user的得分,这既体现了KG的语义信息,又体现了user对relation的个性化偏好
注意:实体的邻居的大小各不相同,最坏情况下可能过大。
因此,对每个节点,进行固定大小的邻域的采样,将其作为receptive field,这使得KGCN的成本可预测。
1个给定实体的邻域的定义,还可以分层的扩展到多个跳跃点,以对high-order entity dependencies进行建模,并捕捉user的潜在long-distance兴趣。
Related Work
通常来说,GCN分为spectral methods、non-spectral methods
- Spectral methods在spectral space上表示graph、进行卷积操作:
- Bruna:在Fourier domain上定义卷积,并计算图的拉普拉斯算子(graph Laplacian)的特征分解(eigendecomposition)
- Defferrard:通过图的拉普拉斯算子的Chebyshev展开近似估计卷积核
- Kipf:propose a convolutional architecture via a localized first-order approximation of spectral graph convolutions.
- non-spectral methods直接在原始graph上进行操作,并且对groups of nodes定义卷积操作。为了处理大小不同的邻域,并保持CNN的权重共享的属性,研究人员提出:为每个节点的度学习一个权重矩阵,从graphs中提取locally connected regions或者采样一组固定大小的邻居集作为support size
KGCN
1. Problem Formulation
M个user的集合 U = [ u 1 , u 2 , . . . , u M ] U = [u_1,u_2,...,u_M] U=[u1,u2,...,uM]; N个item的集合 V = [ v 1 , v 2 , . . . , v N ] V = [v_1,v_2,...,v_N] V=[v1,v2,...,vN]
user-item交互矩阵 Y Y Y, y u v = 1 y_{uv}=1 yuv=1表明u与v发生交互
知识图谱 G G G由三元组 ( h , r , t ) (h,r,t) (h,r,t)组成
目的Aim:给定user-item交互矩阵 Y Y Y、知识图谱 G G G,预测u是否对v有潜在的兴趣(u、v之前未发生交互)
目标Goal:学习一个prediction function: y u v h a t = F ( u , v ∣ θ , Y , G ) y_{uv}^{hat} = F(u,v | \theta,Y,G) yuvhat=F(u,v∣θ,Y,G), y u v h a t y_{uv}^{hat} yuvhat表示u与v发生交互的概率, θ \theta θ表示函数F的模型参数
2. KGCN Layer
KGCN用于捕捉KG中的实体之间的高阶结构接近度high-order structural proximity。
本节从描述KGCN layer开始:
对于给定user u、item v的一个候选对,使用:
- N ( v ) N(v) N(v)表示直接连接到v的实体的集合
- r e i , e j r_{e_i,e_j} rei,ej表示实体 e i e_i ei、 e j e_j ej之间的关系
- 函数 g g g(比如内积)用来计算一个user、一个relation之间的得分: π r u = g ( u , r ) \pi_r^u = g(u,r) πru=g(u,r),u、r分别是user u、relation r的表示。
- π r u \pi_r^u πru表征了r对于u的重要性(比如,一个user可能喜欢movies that share the same “star" with his historically liked ones,另一个user可能更关心电影的类型)
为了表征item v的拓扑邻近结构topological proximity structure,可以计算v的邻域的线性组合:
其中,user-relation score π r v , e u \pi _{r_{v,e}}^u πrv,eu在计算一个实体的邻域表示时,充当了personalized filters(因为会针对特定user的得分,对邻居with bias 进行汇总)
个人理解:
公式(2)中item v的拓扑邻近结构 v N ( v ) u v_{N(v)}^u vN(v)u可以理解为:对每个连接到item v的实体e,将它的表示与user-relation score相乘,再求和得到 topological proximity structure of item v的表示。
π r v , e u \pi _{r_{v,e}}^u πrv,eu表示: v与其连接实体之间的关系 对user u的重要性
在实际的KG中, N ( e ) N(e) N(e)的大小可能在所有实体上都发生着显著变化。为了使每个batch的计算模式保持固定、高效,为每个实体采样一组固定大小的邻居集合,而不是使用全部邻居。
特别的,计算实体v的邻域的表示,可以得到 v S ( v ) u v_{S(v)}^u vS(v)u,其中 S ( v ) ≜ [ e ∣ e ∼ N ( v ) ] S(v) ≜ [e|e ∼ N(v)] S(v)≜[e∣e∼N(v)],并且 ∣ S ( v ) ∣ = K |S(v)|=K ∣S(v)∣=K是一个可配置的常数。KGCN中, S ( v ) S(v) S(v)叫作实体v的(single-layer)接受场receptive field,因为v的最终表示对这些位置十分敏感。
下图为某个给定实体的2-layer receptive field,其中K=2:
KGCN layer的最后一个步骤是:将实体表示v、它的邻域表示 v S ( v ) u v_{S(v)}^u vS(v)u聚合到单个向量上,有三种类型的聚合器:
-
Sum aggregator:对两个表示向量求和,后面再应用一个非线性变换
a g g s u m = σ ( W ⋅ ( v + v S ( v ) u ) + b ) agg_{sum} = \sigma (W \cdot (v + v_{S(v)}^u) + b) aggsum=σ(W⋅(v+vS(v)u)+b)
-
Concat aggregator:先连接两个表示向量
a g g c o n c a t = σ ( W ⋅ c o n c a t ( v , v S ( v ) u ) + b ) agg_{concat} = \sigma (W \cdot concat(v, v_{S(v)}^u) + b) aggconcat=σ(W⋅concat(v,vS(v)u)+b)
-
Neighbor aggregator:直接把实体v的邻域的表示作为输出表示
a g g n e i g h b o r = σ ( W ⋅ v S ( v ) u + b ) agg_{neighbor} = \sigma (W \cdot v_{S(v)}^u + b) aggneighbor=σ(W⋅vS(v)u+b)
聚合操作在KGCN中很关键,因为item的表示通过聚合,与它的邻居绑定在一起。
3. Learning Algorithm
通过一个KGCN layer,一个实体的最终表示取决于它自己、它的直接邻居(命名为1-order实体表示)
将KGCN从1层扩展到多层(可深入、广泛的探究用户的潜在兴趣):
- 将每个实体的初始表示(0-order表示)传播到它的邻居,可以得到1-order实体表示
- 重复此过程,进一步传播、聚合1-order表示,可以得到2-order表示
通常来说,一个实体的h-order表示,是它自身的初始表示、h跳邻居 的混合。(这是对KGCN非常重要的属性)
Algorithm 1表述了 上述步骤的形式化描述,H表示receptive field的最大深度(或者说,聚合的迭代次数),表示向量附加的后缀 [ h ] [h] [h]表示h-order。
- 对于一个给定的user-item对(line 2),首先计算v的receptive field M M M(以一种迭代的、layer-by-layer的方式计算,line 3,13-19)
- 然后,重复H次聚合操作(第5行):
- 在第h个迭代中,先计算出每个实体 e ∈ M [ h ] e \in M[h] e∈M[h]的邻域表示(line 7)
- 将它与它自己的表示 e u [ h − 1 ] e^u[h-1] eu[h−1]进行聚合,得到下一个迭代所需的表示(line 8)
- 最终的H-order entity presentation表示为 v u v^u vu(line 9)
- 将 v u v^u vu与user的表示u一起作为函数 f f f的输入,来预测概率: y u v h a t = f ( u , v u ) y_{uv}^{hat} = f(u,v^u) yuvhat=f(u,vu)
-
下图表示了KGCN算法的一个迭代:
这当中,实体表示 v u [ h ] v^u[h] vu[h]、给定节点的邻域表示(绿色节点)混合在一起,以形成下一次迭代的表示(蓝色节点)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cfncerfJ-1615360141609)(https://516000.xyz/images/2021/02/27/2021-02-27-15.30.41.png)]
Algorithm 1遍历了所有可能的user-item对(line 2)
为使得计算更高效,在训练时采用了负采样策略。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b173TnCK-1615360141609)(https://516000.xyz/images/2021/03/10/2021-03-10-10.29.09.png)]
- Loss Function:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BQUQ2CAp-1615360141610)(https://516000.xyz/images/2021/02/27/2021-02-27-15.37.11.png)]