G-mixup论文阅读

论文阅读：G-mixup：Graph Data Augmentation for Graph Classification

摘要

mixup数据增强在图像领域获得了不错的效果，但是在图数据中仍然有很多挑战。他有这么几个难点：1.不同的图有不同的结点个数；2.图数据并不是对齐的；3.图在非欧空间中有唯一的拓扑结果。所以直接使用mixup是不行的，作者提出了G-mixup，用于图的数据增强。他的主要思想是，同属于一类的graph生成同一个graphon。不同于直接在graph上进行操作，作者对于生成的在欧式空间的graphon进行扰动，混合。然后根据混合的graphon合成新的混合图。大量的实验表面G-mixup可以提高GNN的泛化能力和鲁棒性

1.Mixup数据增强

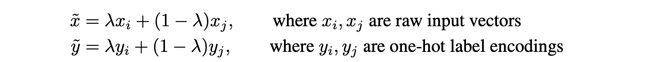
mixup的思想很简单，这里的$\lambda$是服从beta分布，范围为(0,1)的连续概率密度函数。因为图像数据都是方阵，所以很好进行变换。思想简单但是取得了很不错的效果。作者就想着能不能把mixup迁移到图的数据上来。
但是有几个难点：数据集中的每幅图结点个数不一样，他的邻接矩阵大小也不一样。
图数据是在非欧空间中有唯一的拓扑结果，和图像数据不一样
图的数据不对齐，很难匹配带不同图里的结点。
所以提出了G-mixup。它属于生成模型。通过生成新的数据来进行数据增强。主要用于graph classification task

2.G-mixup implement

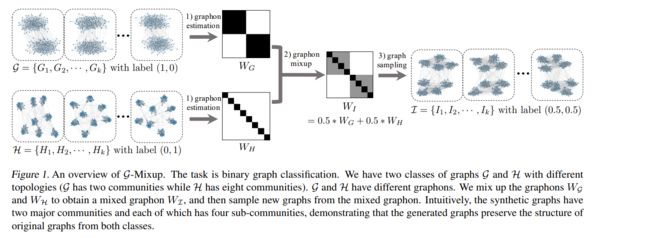
这是G-mixup的流程图。主要分为四个部分，如下图所示：

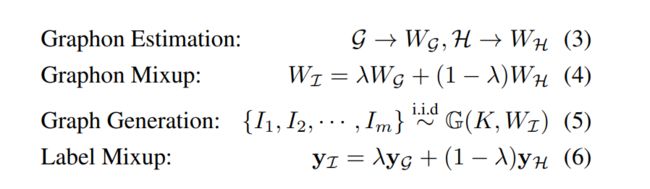
上面两幅图可以一起看。他的流程主要分为四个部分。
第一步是Graphon Estimation。暂时可以理解为将同属于一个类别的图由非欧空间映射到欧式空间，形成方阵，其中每个元素是node i和node j之间有边的概率。
第二步是Graphon Mixup 。不直接对graph进行变换，而是变换每一类图生成的graphon。
第三步是根据混合的graphon生成新的图
第四步是对生成图进行label
首先我们看第一步

Graphon Estimation

要理解这个，首先要理解什么是Graphon。Graphon的中文翻译是图极限，属于图论的另一大问题。我翻了很多中文社区资料，几乎没有讲graphon的，只有国外有资料，我翻了很多，看得属实是痛不欲生。我尽力把我所理解的graphon表达出来。如果有大佬有比较好的资料可以发在评论区，感激不尽。如有错误还请包涵。
graphon是graph和function的结合，中文叫图极限。举个例子：假设我们对于数的了解仅限于有理数，那么对于无理数，比如$\sqrt{2}$ 我们可以用1.4 1.41 1.414这种有理数数列去无线逼近他。但是我们现在有实数，填补了这个数轴的空缺。从这个角度来说，实数是有理数的极限。
同样的，图是类似有理数的离散对象，一连串的图也可以收敛为一个极限对象，这就是图极限。

直观一点，这是一张图，旁边是他的邻接矩阵。假设继续按照这种规律不断的加边，加点，那么当图的点和边趋于无穷时，就可以生成最右边这张图。这是图极限的一个直观的例子。
反过来，给定图极限，可以把他变成随机图的生成模型。
这个就是graphon estimation 的理论基础。

graphon 在理论上是存在的，但是他却很难直接去求出来。因为他是在点和边都趋于无穷的时候所趋近的一个模式，所以只能用一些算法去逼近。
好在，有理论已经证明，我们可以使用step function(阶梯函数)来无限逼近graphon。
step function的一般表达式是这个

$W_{k,k^{\prime }}$是属于0-1之间的数，$I_{p_k\ast p_k(x,y)}$是符号函数，如果(x,y)属于$p_k\ast p_k$就是1，不然就是0.这里的$p_k$我个人理解是他把0-1之前分成k份，也就是说，当(x,y)是（1/k,1/k）,或者(1/k,2/k）的时候，才为1，否则为零。这里的x，y都是连续的值。具体求解graphon的算法我在中文社区也没有找到，在外文社区里有，我看得很头疼，就放弃了。
在这篇论文中，作者告诉我们，生成的graphon可以看成一个连续有界且对称的矩阵W ，w[i,j]取值范围是（0,1）其值是node i和node j有边的概率。
W是K*K的方阵，K是每一类图的average node。所以(1/k,2/k）才为1，我觉得是在这里体现的。
这是他Graphon Estimation的结果图
每一个类别生成一张graphon

那么我有个问题。就是说，我生成的graphon是k阶方阵，k是average node，但是作者在论文里说graphon可以生成无限维图，我觉得具体在实操的时候是做不到的。也是因为对graphon的原理不太懂，按下不表。

Graphon Mixup

生成每一类的graphon之后，对graphon进行混合，这一步比较容易，因为这里相当于是对矩阵进行加减运算。不说了

Synthetic Graphs Generation

根据混合的graphon生成图，作者说的是：1、随机取样k个点。我个人不太知道这里是怎么做的，因为他的graphon只有k个点（k是average nodes）。或者说这里的k是小于W里的k。2.生成邻接矩阵A，其中a[i,j]是1还是0，是由w[i,j]决定的。这里是一个二项分布，有w[i,j]的概率生成边，有1-w[i,j]的概率不生成。3、node feature生成。在graphonestimation时对齐Node feature，使用average pooling生成graphon node feature。生成的nodefeature和graphon node feature。
这里对node feature生成描述非常少，只有短短几行字，不能窥得他具体的操作，这作者也没有源码，就更不知道了。
这是他的生成图结果。

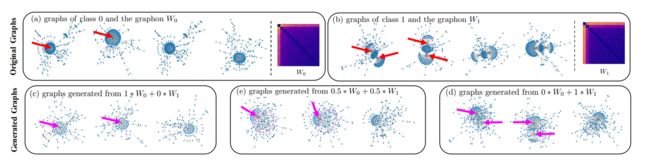
我们可以看到，一个数据集里有两类，class 1是有一个超级点(一个点有很多条边和其他点进行连接)，class2有两个超级点。他生成的图还是可以根据不同类的graphon的贡献对图的拓扑信息进行不错的刻画的。

Label mixup

这里也很简单，和原来的mixup是一样的，按下不表

3.experiment

使用G-mixup对数据进行增强之后，做一些实验，取得了一些效果

仅从test来看，他们的oss都是更少的。

作者还和其他的一些数据增强的方法进行比较，效果也还可以。

4.Discussion

这篇文章是被ICML2022收录的，但是他在iclr的时候是被拒收的，分数并不高。我看的版本是22年2月份的预刊，可能和最终被收录的版本不一样。但是我就从这个预刊的来看，我有这么几个问题。
1.graphon的原理和估计没有特别看懂，文章是怎么求出来的，并没有很清楚地说明，他在附录里的东西并不比原文好到哪里去。
你graphon没搞懂，后面他怎么反推回去生成新的图其实也只能一知半解。比如取样k个点，是怎么取的。
2.这种数据增强的方式应该是只能简单生成无向图，对于有向图和复杂图应该是没有办法的
3.根据他的图展示的，我们可以看到这个方法对构造拓扑信息还是挺有用的，但是对node feature的生成我觉得讲得不是很清楚，寥寥几行字，而且这方面可不可以有更好的办法。
论文链接