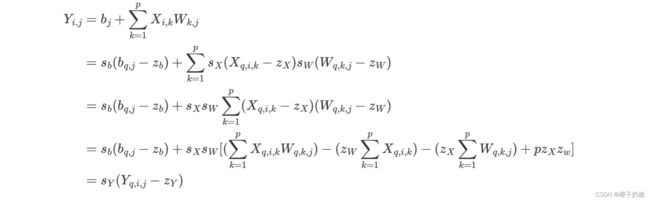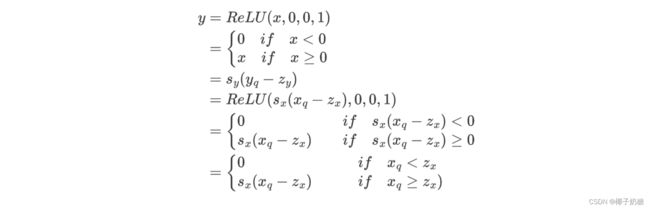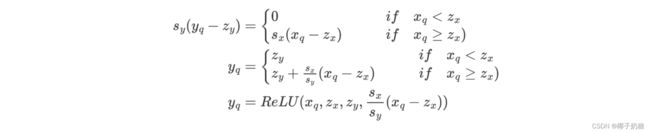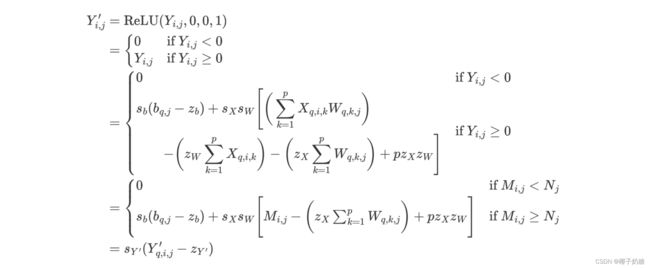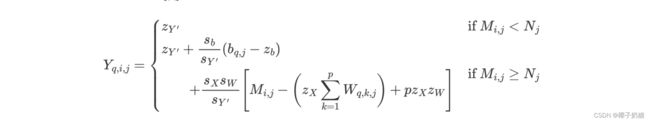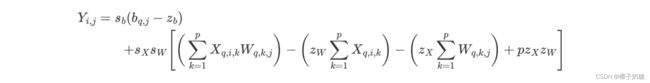神经网络的量化
神经网络的量化
文章目录
-
-
- 神经网络的量化
-
- Reference
- Introduction
- Quantization
-
- Quantization Mapping
- Value Clipping
- Affine Quantization Mapping
- Scale Quantization Mapping
- Quantized Matrix Multiplication
-
- Quantized Matrix Multiplication Mathematics
- Example
- Quantized Deep Learning Layers
-
- Quantized ReLU
- Example
- Layer Fusions
- Neural Networks Integer Quantization Modes
-
- Dynamic Quantization
- Static Quantization
- Quantization Aware Training
-
Reference
- Quantization for Neural Networks
Introduction
- 量化：用低精度来表示高精度的数，如：FP16/INT8表示FP32这种。
- 目前为止，主要的深度学习框架，如TensorFlow和PyTorch，已经原生支持量化。用户已经成功地使用了内置的量化模块，而不知道它到底是如何工作的。在Reference中的这篇文章用数学的角度阐述了神经网络的量化，下文是个人对其的理解。
- 其实某种程度上来说，可以看做这篇文章的翻译
- 由于CSDN对latex公式支持不全，所以部分公式就用截图了。。
Quantization
Quantization Mapping
-
首先定义浮点数 x ∈ [ α , β ] x \in [\alpha, \beta] x∈[α,β]，量化后的整型 x q ∈ [ α q , β q ] x_q \in [\alpha_q, \beta_q] xq∈[αq,βq]
-
然后定义一个线性表达式来表示反量化的过程，然后下一行是量化的过程
-
x = c ( x q + d ) x q = r o u n d ( x ∗ 1 c − d ) x = c(x_q + d) \\ x_q = round(x * \frac{1}{c} - d) x=c(xq+d)xq=round(x∗c1−d)
-
可以注意到量化其实有一个round取整的过程，这里就是误差的来源
-
-
然后cd的推导与量化前后的范围有关，当我们希望从 β \beta β量化到 β q \beta_q βq的时候，也会有一个线性量化的方程，即：
-
β = c ( β q + d ) α = c ( α q + d ) \beta = c (\beta_q + d) \\ \alpha = c (\alpha_q + d) β=c(βq+d)α=c(αq+d)
-
然后求解一下就是：
-
c = β − α β q − α q d = α β q − β α q β − α c = \frac{\beta - \alpha}{\beta_q - \alpha_q} \\ d = \frac{\alpha \beta_q - \beta\alpha_q}{\beta - \alpha} c=βq−αqβ−αd=β−ααβq−βαq
-
-
作者提到我们需要保证浮点数中的0在量化后没有误差（不是0，而是没有误差，误差就是被round舍去的部分），其实意思是要求d要有一个取值范围
- 即：
- 按照上述的要求，你会发现d需要是一个整数
-
然后按照惯例替换字母，c = s , d = z，下文会直接用s和z表示
Value Clipping
-
这一节主要是讲的当数越界的时候该怎么办？——当然是取边界值～
-
x q = c l i p ( r o u n d ( 1 s x + z ) , α q , β q ) x_q = clip (round(\frac{1}{s}x + z), \alpha_q, \beta_q) xq=clip(round(s1x+z),αq,βq)
-
这里的clip就是处理待量化数的越界情况的函数，定义为：
-
c l i p ( x , l , u ) = { l i f x < l x i f l ≤ x ≤ u u i f x > u clip(x,l,u) = \begin{cases} l \quad if \quad x < l \\ x \quad if \quad l \leq x \leq u \\ u \quad if \quad x > u \end{cases} clip(x,l,u)=⎩⎪⎨⎪⎧lifx<lxifl≤x≤uuifx>u
Affine Quantization Mapping
- 仿射量化映射，即上面讨论的方式
Scale Quantization Mapping
-
规模量化映射，即对称的量化映射，是affine quantization mapping的特例
-
当 α = − β \alpha=−\beta α=−β时，我们有：
-
α q = − β q r o u n d ( α β q − β α q β − α ) = 0 \alpha_q=−\beta_q \\ round(\frac{\alpha\beta_q - \beta \alpha_q}{\beta - \alpha}) = 0 αq=−βqround(β−ααβq−βαq)=0
-
Quantized Matrix Multiplication
- 量化矩阵乘法，它的意义在于，整数积矩阵可以通过整数积矩阵的scale和zero points(s和d)转换回浮点矩阵，在数值上几乎是等价的。如果我们要做一个输入和输出都是浮点数的矩阵乘法
Quantized Matrix Multiplication Mathematics
-
定义矩阵运算为（他是线性的）： Y = X W + b ; X ∈ R m ∗ p W ∈ R p ∗ n ] b ∈ R n Y ∈ R m ∗ n Y=XW+b; \quad X \in \mathcal R ^{m*p} \quad W \in \mathcal R^{p*n]} \quad b \in \mathcal R ^n \quad Y \in \mathcal R ^{m*n} Y=XW+b;X∈Rm∗pW∈Rp∗n]b∈RnY∈Rm∗n ，
-
此时对某个结果元素 Y i , j Y_{i,j} Yi,j，公式为：
-
Y i . j = b j + ∑ k = 1 p X i , k W k , j Y_{i.j} = b_j + \sum_{k=1}^p X_{i,k}W_{k,j} Yi.j=bj+k=1∑pXi,kWk,j
-
对于 Y i , j Y_{i,j} Yi,j我们需要分别进行p次的浮点数加法和乘法，那么对于整个矩阵，计算复杂度为O(mnp)，而且是浮点运算。
-
对于计算机底层的设计，一般来说浮点数的计算的复杂程度是远大于整数的（当然FP16相对于FP32算起来是快一点的）
-
-
于是问题就变成了：对于矩阵运算，我们能否用量化后的数值完成（在误差可接受范围内）
-
还是以元素 Y i , j Y_{i,j} Yi,j为例：我们将上文推导的量化公式代入，我们可以写出求解该元素的反量化公式：
-
下标q表示量化后的值，s是scale，即上文的c，z是zero points，即上文的d
-
因此 Y q , i , j Y_{q,i,j} Yq,i,j可以表示为：
-
Y q , i , j = z Y + s b s Y ( b q , j − z b ) + s X s W s Y [ ( ∑ k = 1 p X q , i , k W q , k , j ) − ( z W ∑ k = 1 p X q , i , k ) − ( z X ∑ k = 1 p W q , k , j ) + p z X z w ] Y_{q,i,j} = z_Y + \frac{s_b}{s_Y}(b_{q,j}-z_b) + \frac{s_Xs_W}{s_Y}[(\sum_{k=1}^p X_{q,i,k}W_{q,k,j}) - (z_W\sum_{k=1}^p X_{q,i,k}) - (z_X\sum_{k=1}^p W_{q,k,j}) + pz_Xz_w] Yq,i,j=zY+sYsb(bq,j−zb)+sYsXsW[(k=1∑pXq,i,kWq,k,j)−(zWk=1∑pXq,i,k)−(zXk=1∑pWq,k,j)+pzXzw]
- 其中这些部分是常数，可以直接在inference之前就计算完成然后储存好：
-
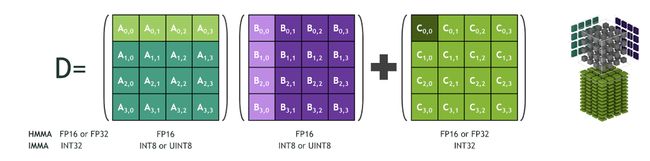
然后剩下的 ∑ k = 1 p X q , i , k W q , k , j \sum_{k=1}^p X_{q,i,k}W_{q,k,j} ∑k=1pXq,i,kWq,k,j，运算的时候是量化后的形式（如INT8），计算量相对而言就比浮点数下降了很多，且如果对应量化后的形式有特定的硬件支持，会更加快，such as NVIDIA Tensor Core and Tensor Core IMMA operations
-
-
由于s与z是常量，对于这些乘法，可能会有一些特殊的编译时优化（如直接在算出所有结果，然后用检索的方式查找，这比直接计算快速的多，但是一般是在这个数的范围有限的时候才这么做，否则得不偿失）。
-
Example
- 还没跑过，看代码大致就是验证举证中的量化是否如上述理论说
- 就是先计算和后量化，与先量化后计算，结果对比
import numpy as np
def quantization(x, s, z, alpha_q, beta_q):
x_q = np.round(1 / s * x + z, decimals=0)
x_q = np.clip(x_q, a_min=alpha_q, a_max=beta_q)
return x_q
def quantization_int8(x, s, z):
x_q = quantization(x, s, z, alpha_q=-128, beta_q=127)
x_q = x_q.astype(np.int8)
return x_q
def dequantization(x_q, s, z):
x = s * (x_q - z)
x = x.astype(np.float32)
return x
def generate_quantization_constants(alpha, beta, alpha_q, beta_q):
# Affine quantization mapping
s = (beta - alpha) / (beta_q - alpha_q)
z = int((beta * alpha_q - alpha * beta_q) / (beta - alpha))
return s, z
def generate_quantization_int8_constants(alpha, beta):
b = 8
alpha_q = -2**(b - 1)
beta_q = 2**(b - 1) - 1
s, z = generate_quantization_constants(alpha=alpha,
beta=beta,
alpha_q=alpha_q,
beta_q=beta_q)
return s, z
def quantization_matrix_multiplication_int8(X_q, W_q, b_q, s_X, z_X, s_W, z_W,
s_b, z_b, s_Y, z_Y):
p = W_q.shape[0]
Y_q_simulated = (
z_Y + (s_b / s_Y * (b_q.astype(np.int32) - z_b)).astype(np.int8) +
((s_X * s_W / s_Y) *
(np.matmul(X_q.astype(np.int32), W_q.astype(np.int32)) -
z_W * np.sum(X_q.astype(np.int32), axis=1, keepdims=True) -
z_X * np.sum(W_q.astype(np.int32), axis=0, keepdims=True) +
p * z_X * z_W)).astype(np.int8)).astype(np.int8)
return Y_q_simulated
def main():
# Set random seed for reproducibility
random_seed = 0
np.random.seed(random_seed)
# Random matrices
m = 2
p = 3
n = 4
# X
alpha_X = -100.0
beta_X = 80.0
s_X, z_X = generate_quantization_int8_constants(alpha=alpha_X, beta=beta_X)
X = np.random.uniform(low=alpha_X, high=beta_X,
size=(m, p)).astype(np.float32)
X_q = quantization_int8(x=X, s=s_X, z=z_X)
# W
alpha_W = -20.0
beta_W = 10.0
s_W, z_W = generate_quantization_int8_constants(alpha=alpha_W, beta=beta_W)
W = np.random.uniform(low=alpha_W, high=beta_W,
size=(p, n)).astype(np.float32)
W_q = quantization_int8(x=W, s=s_W, z=z_W)
# b
alpha_b = -500.0
beta_b = 500.0
s_b, z_b = generate_quantization_int8_constants(alpha=alpha_b, beta=beta_b)
b = np.random.uniform(low=alpha_b, high=beta_b,
size=(1, n)).astype(np.float32)
b_q = quantization_int8(x=b, s=s_b, z=z_b)
# Y
alpha_Y = -3000.0
beta_Y = 3000.0
s_Y, z_Y = generate_quantization_int8_constants(alpha=alpha_Y, beta=beta_Y)
Y_expected = np.matmul(X, W) + b
Y_q_expected = quantization_int8(x=Y_expected, s=s_Y, z=z_Y)
print("Expected Y:")
print(Y_expected)
print("Expected Y_q:")
print(Y_q_expected)
Y_q_simulated = quantization_matrix_multiplication_int8(X_q=X_q,
W_q=W_q,
b_q=b_q,
s_X=s_X,
z_X=z_X,
s_W=s_W,
z_W=z_W,
s_b=s_b,
z_b=z_b,
s_Y=s_Y,
z_Y=z_Y)
Y_simulated = dequantization(x_q=Y_q_simulated, s=s_Y, z=z_Y)
print("Y from Quantized Matrix Multiplication:")
print(Y_simulated)
print("Y_q from Quantized Matrix Multiplication:")
print(Y_q_simulated)
if __name__ == "__main__":
main()
Quantized Deep Learning Layers
- 除了卷积，激活函数、归一化等非线性函数也需要面临量化问题，毕竟如果你的卷积是量化后的，那么其他部分也应当对应起来，否则输出就不一定对应了。
- 最原始的解决方法是在进行此类层之前先进行去量化，那么就没有这个问题了，但是量化与去量化是存在一定成本的，这么做会导致推理速度的下降。
Quantized ReLU
-
ReLU更一般化的定义:
-
R e L U ( x , z x , z y , k ) = { z y i f x < z x z y + k ( x − z x ) i f x ≥ z x ReLU(x,z_x, z_y, k) = \begin{cases} z_y \quad if \quad x < z_x \\ z_y + k(x - z_x) \quad if \quad x \geq z_x \end{cases} ReLU(x,zx,zy,k)={zyifx<zxzy+k(x−zx)ifx≥zx
-
当 z y = z x = 0 z_y = z_x = 0 zy=zx=0 && $ k=1$的时候就变成了：
-
R e L U ( x , 0 , 0 , 1 ) = { 0 i f x < 0 x i f x ≥ 0 ReLU(x,0, 0, 1) = \begin{cases} 0 \quad if \quad x < 0 \\ x \quad if \quad x \geq 0 \end{cases} ReLU(x,0,0,1)={0ifx<0xifx≥0
-
就是常用的那个ReLU
-
-
接下来我们量化ReLU。同样地，我们先写出反量化的等式：
-
上面的等式大致想表达的意思是这样的，我们希望量化后的输入进入量化后的ReLU就是量化后的y
- 因此有了对输出y的量化等式： y = s y ( y q − z y ) y = s_y(y_q - z_y) y=sy(yq−zy)
- 然后当输入量化后的进入ReLU的输出，我们希望这一部分也尽可能接近y，由此可以得到 y q y_q yq的等式
-
y q y_q yq的等式为：
- 于是乎就得到了量化版的ReLU（其实就是各种权重怎么计算的问题）
-
Example
import numpy as np
def quantization(x, s, z, alpha_q, beta_q):
x_q = np.round(1 / s * x + z, decimals=0)
x_q = np.clip(x_q, a_min=alpha_q, a_max=beta_q)
return x_q
def quantization_int8(x, s, z):
x_q = quantization(x, s, z, alpha_q=-128, beta_q=127)
x_q = x_q.astype(np.int8)
return x_q
def quantization_uint8(x, s, z):
x_q = quantization(x, s, z, alpha_q=0, beta_q=255)
x_q = x_q.astype(np.uint8)
return x_q
def dequantization(x_q, s, z):
x = s * (x_q - z)
x = x.astype(np.float32)
return x
def generate_quantization_constants(alpha, beta, alpha_q, beta_q):
# Affine quantization mapping
s = (beta - alpha) / (beta_q - alpha_q)
z = int((beta * alpha_q - alpha * beta_q) / (beta - alpha))
return s, z
def generate_quantization_int8_constants(alpha, beta):
b = 8
alpha_q = -2**(b - 1)
beta_q = 2**(b - 1) - 1
s, z = generate_quantization_constants(alpha=alpha,
beta=beta,
alpha_q=alpha_q,
beta_q=beta_q)
return s, z
def generate_quantization_uint8_constants(alpha, beta):
b = 8
alpha_q = 0
beta_q = 2**(b) - 1
s, z = generate_quantization_constants(alpha=alpha,
beta=beta,
alpha_q=alpha_q,
beta_q=beta_q)
return s, z
def relu(x, z_x, z_y, k):
x = np.clip(x, a_min=z_x, a_max=None)
y = z_y + k * (x - z_x)
return y
def quantization_relu_uint8(x, s_x, z_x, s_y, z_y):
y = relu(x=X_q, z_x=z_X, z_y=z_Y, k=s_X / s_Y)
y = y.astype(np.uint8)
return y
if __name__ == "__main__":
# Set random seed for reproducibility
random_seed = 0
np.random.seed(random_seed)
# Random matrices
m = 2
n = 4
alpha_X = -60.0
beta_X = 60.0
s_X, z_X = generate_quantization_int8_constants(alpha=alpha_X, beta=beta_X)
X = np.random.uniform(low=alpha_X, high=beta_X,
size=(m, n)).astype(np.float32)
X_q = quantization_int8(x=X, s=s_X, z=z_X)
alpha_Y = 0.0
beta_Y = 200.0
s_Y, z_Y = generate_quantization_uint8_constants(alpha=alpha_Y,
beta=beta_Y)
Y_expected = relu(x=X, z_x=0, z_y=0, k=1)
Y_q_expected = quantization_uint8(x=Y_expected, s=s_Y, z=z_Y)
print("X:")
print(X)
print("X_q:")
print(X_q)
print("Expected Y:")
print(Y_expected)
print("Expected Y_q:")
print(Y_q_expected)
Y_q_simulated = quantization_relu_uint8(x=X,
s_x=s_X,
z_x=z_X,
s_y=s_Y,
z_y=z_Y)
Y_simulated = dequantization(x_q=Y_q_simulated, s=s_Y, z=z_Y)
print("Y from ReLU:")
print(Y_simulated)
print("Y_q from Quantized ReLU:")
print(Y_q_simulated)
Layer Fusions
-
层融合在工业界会用的比较多，比如Conv2D-ReLU和Conv2D-BatchNorm-ReLU等神经网络层的组合，通常会进行层融合。
-
以Conv2D-ReLU的融合为例：
- 如果没有融合，我们在计算量化后的Conv2D+ReLU的结果的时候需要三组scale&zero point参数（s&z，输入一组，输出一组，同时层与层之间的输入输出参数时候共享的，因此是三组，其实这么理解更好：每一层需要一组，并且输入如果不是量化后的形式也需要一组，这样没融合之前的两层就是需要三组）
- 那么融合之后，由于Conv2D-ReLU可以看成一层，那么量化的时候就只需要一组参数就够了
-
数学上的表达，简便起见ReLU就采用常见的形式
-
定义： Y i , j Y_{i,j} Yi,j是Conv2D的输出， Y i , j ′ Y^{\prime}_{i,j} Yi,j′是Conv2D-ReLU的最终输出， Y q , i , j ′ Y^{\prime}_{q,i,j} Yq,i,j′是量化后的最终输出
-
此时我们将 Y i , j Y_{i,j} Yi,j作为ReLU的输入，根据上文提到的推理将 Y i , j Y_{i,j} Yi,j展开，就可以写出下面反量化的等式：
-
为简便起见，定义 M i , j M_{i,j} Mi,j和 N j N_j Nj
-
M i , j = ( ∑ k = 1 p X q , i , k W q , k , j ) − ( z W ∑ k = 1 p X q , i , k ) M_{i,j} = \bigg( \sum_{k=1}^{p} X_{q,i,k} W_{q, k,j} \bigg) - \bigg( z_W \sum_{k=1}^{p} X_{q,i,k} \bigg) Mi,j=(k=1∑pXq,i,kWq,k,j)−(zWk=1∑pXq,i,k)
-
N j = ( z X ∑ k = 1 p W q , k , j ) − p z X z W + s b s X s W ( b q , j − z b ) N_{j} = \bigg( z_X \sum_{k=1}^{p} W_{q, k,j} \bigg) - p z_X z_W + \frac{s_b}{s_X s_W} (b_{q, j} - z_b) Nj=(zXk=1∑pWq,k,j)−pzXzW+sXsWsb(bq,j−zb)
-
然后老套路利用等式关系解出 Y q , i , j ′ Y^{\prime}_{q,i,j} Yq,i,j′
-
- 如果对照之前推理矩阵量化的化，我们会发现这个公式中少了 s Y , z Y s_Y,z_Y sY,zY这一组参数，可见当融合之后，需要的s&z参数就少了(这里是变成了两组)
Neural Networks Integer Quantization Modes
- 神经网络的量化模式
- 神经网络一般有三种模式:整数量化、动态量化、(训练后)静态量化和量化感知训练。三种模式的特点总结如下。通常在实践中最常见的是静态量化和量化感知训练，因为它们在实践中是三种模式中速度最快的。
Dynamic Quantization
-
在动态量化的神经网络推理中，尽可能多地使用整数运算。在推断运行之前，权重被量化为整数。然而，由于神经网络不知道输出或激活张量的scale和zero point，因此输出或激活张量必须是一个浮点张量。
-
而当得到输出之后，就可以通过这个浮点张量来算出scale和zero point，在运行时动态将结果量化成INT张量，这就是动态量化。
- 以矩阵量化为例，由于我们不知道 s Y , z Y s_Y,z_Y sY,zY，所以计算的时候必须先计算出浮点结果 Y i , j Y_{i,j} Yi,j：
- 而当我们又了 Y i , j Y_{i,j} Yi,j的结果则可以通过计算得出 s Y , z Y s_Y,z_Y sY,zY（通过他的边界），然后由此计算出 Y q , i , j Y_{q,i,j} Yq,i,j
-
动态量化的优点是，在推断之前，我们不需要任何数据来进行任何类型的校准，但是scale和zero point必须动态计算。
Static Quantization
- 与动态量化不同的是，静态量化决定了尺度，所有激活张量的零点都是预先计算的。因此，计算scale和zero point的开销被消除了。于是计算的时候就少了一步转换的步骤。
- 确定所有激活张量的标度和零点的方法很简单。给定一个浮点神经网络，我们只需使用一些代表性的未标记数据运行神经网络，收集所有激活层的分布统计信息。然后，我们可以使用分布统计数据，使用本文前面描述的数学方程来计算scale和zero point。
- 在推理过程中，由于所有的计算都是使用整数运算无缝进行的，因此推理性能是最快的。唯一的缺点是我们必须准备有代表性的未标记数据。如果数据不具有代表性，则推断时计算的尺度和零点可能不能反映真实的情景，从而影响推断的准确性。
Quantization Aware Training
-
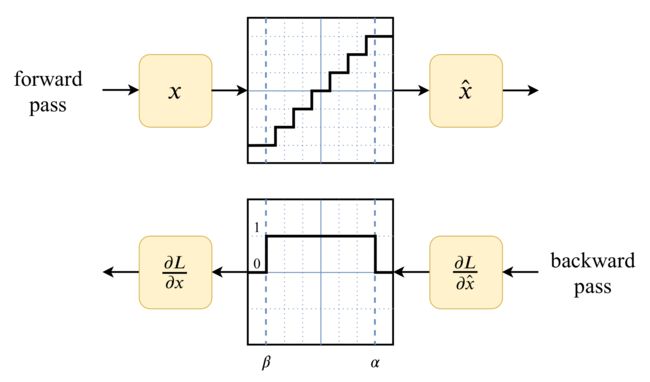
量化与反量化这一套过程是存在一个误差的，在数学上表达是: x = f d ( f q ( x , s x , z x ) , s x , z x ) + Δ x x = f_d \big(f_q(x, s_x, z_x), s_x, z_x\big) + \Delta_x x=fd(fq(x,sx,zx),sx,zx)+Δx。其中 f d , f q f_d,f_q fd,fq分别表示反量化和量化函数，误差就是 Δ x \Delta_x Δx
-
于是就有个idea就是想到在训练的时候就考虑到量化误差的存在，因此这个方法理论上使得模型对推理精度的牺牲较小。
-
具体方式为：
- 在神经网络训练过程中，所有的激活或输出张量和权重张量都是变量。因此，在量化感知训练中，我们为每个变量张量添加了一个量化层和一个去量化层。在数学上,这意味着
-
意思是说我们在训练的时候就加了一个量化的过程，是的模型考虑了量化的损失，但是这种方法往往会导致数变得里三，这意味着我们需要重写反向传播函数（backward）
-
