【应用多元统计分析】-王学民Python画椭圆,主成分分析,特征值处理和可视化(1)
title: “应用多元统计分析”
subtitle: “书上题目”
author: | OLSRR
由于字数限制,本文省去部分数据预览。
图 7.1.1(书)
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 18 14:08:27 2022
@author: olsrr
"""
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import math
import random
fig = plt.figure(0)
ax = fig.add_subplot(111, aspect='equal')
e = Ellipse(xy=(0, 2), width=1.81 * 2, height=0.94 * 2, angle=30)
ax.add_artist(e)
e.set_facecolor("none")
e.set_edgecolor("black")
ax.arrow(-math.sqrt(3), 1, 2 * math.sqrt(3), 2, length_includes_head=True, head_width=0.05, fc='black', ec='black')
ax.arrow(1, 2-math.sqrt(3), -2, 2 * math.sqrt(3), length_includes_head=True, head_width=0.05, fc='black', ec='black')
ax.arrow(-2, 2, 4, 0, length_includes_head=True, head_width=0.05, fc='black', ec='black')
ax.arrow(0, 0, 0, 4, length_includes_head=True, head_width=0.05, fc='black', ec='black')
ax.annotate('x1', xy=(1.8, 1.8), xytext=(1.8, 1.8))
ax.annotate('x2', xy=(-0.2, 3.8), xytext=(-0.2, 3.8))
ax.annotate('y1', xy=(1.7, 2.8), xytext=(1.7, 2.8))
ax.annotate('y2', xy=(-1.2, 3.5), xytext=(-1.2, 3.5))
# plt.scatter(1, 0, s=10, edgecolor='black', facecolor='black')
# 提供的椭圆圆心在(0, 2), 旋转角为30, 椭圆长半轴为1.81,短半轴为0.94
points = 150 # 点的个数
for i in range(points):
x1_flag = -1 if random.randint(0, 1) == 0 else 1 # x正负随机取
x_1 = random.random() * 1.81 * x1_flag # 0-1随机数乘以1.81
x2_flag = -1 if random.randint(0, 1) == 0 else 1 # 与x相同
x_2 = math.sqrt((1 - (x_1/1.81) ** 2) * (0.94**2)) * x2_flag * random.random()
y_1 = x_1 * math.cos(-math.pi/6) + x_2 * math.sin(-math.pi/6)
y_2 = -x_1 * math.sin(-math.pi/6) + x_2 * math.cos(-math.pi/6) + 2
plt.scatter(y_1, y_2, s=10, edgecolor='black', facecolor='black')
plt.xlim(-2, 2)
plt.ylim(0, 4)
ax.grid(True)
plt.axis('off')
# ax.axis[:].set_visible(False)
plt.title(f"points={points}")
plt.show()
7.5
试对例 6.3.7 进行主成分分析。
答案
数据准备:
import pandas as pd
import numpy as np
from pylab import mpl
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.pyplot as mp,seaborn#库准备
model6_3_7 = pd.read_csv("/Users/che/Desktop/应用多元分析/《应用多元统计分析》(第五版,王学民 编著)配书资料/《应用多元统计分析》(第五版)文本数据(以逗号为间隔)/examp6.3.7.csv", encoding='gbk',index_col=0).reset_index(drop=True)
print(model6_3_7)#显示数据
# 身高 手臂长 上肢长 下肢长 体重 颈围 胸围 胸宽
#0 1.000 0.846 0.805 0.859 0.473 0.398 0.301 0.382
#1 0.846 1.000 0.881 0.826 0.376 0.326 0.277 0.415
#2 0.805 0.881 1.000 0.801 0.380 0.319 0.237 0.345
#3 0.859 0.826 0.801 1.000 0.436 0.329 0.327 0.365
#4 0.473 0.376 0.380 0.436 1.000 0.762 0.730 0.629
#5 0.398 0.326 0.319 0.329 0.762 1.000 0.583 0.577
#6 0.301 0.277 0.237 0.327 0.730 0.583 1.000 0.539
#7 0.382 0.415 0.345 0.365 0.629 0.577 0.539 1.000
变量之间的相关系数:
model6_3_7 = pd.read_csv("/Users/che/Desktop/应用多元分析/《应用多元统计分析》(第五版,王学民 编著)配书资料/《应用多元统计分析》(第五版)文本数据(以逗号为间隔)/examp6.3.7.csv", encoding='gbk',index_col=0).reset_index(drop=True)
#print(model6_3_7)
DF6_3_7 = pd.DataFrame(model6_3_7) #建立DataFrame
corr6_3_7 = DF6_3_7.corr() #计算两两的相关系数
print(corr6_3_7)#输出表格
# 身高 手臂长 上肢长 ... 颈围 胸围 胸宽
#身高 1.000000 0.942376 0.928294 ... -0.750988 -0.861523 -0.718088
#手臂长 0.942376 1.000000 0.973950 ... -0.837839 -0.893558 -0.661103
#上肢长 0.928294 0.973950 1.000000 ... -0.809819 -0.895939 -0.710933
#下肢长 0.957582 0.936093 0.925125 ... -0.821523 -0.822690 -0.729807
#体重 -0.762831 -0.871813 -0.842979 ... 0.834378 0.801388 0.516654
#颈围 -0.750988 -0.837839 -0.809819 ... 1.000000 0.614779 0.489246
#胸围 -0.861523 -0.893558 -0.895939 ... 0.614779 1.000000 0.448001
#胸宽 -0.718088 -0.661103 -0.710933 ... 0.489246 0.448001 1.000000
seaborn.heatmap(corr6_3_7, center=0, annot=True, cmap='YlGnBu')#可视化处理
mp.show()
从可视化结果可以看出,一些变量之间的相关系数的绝对值较大,因此可以进行降维处理。
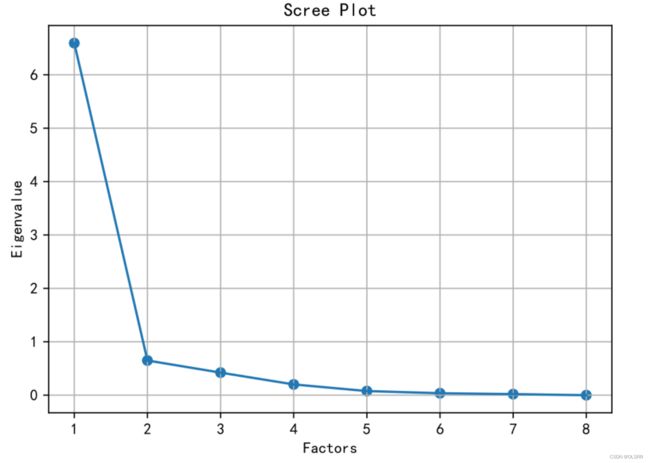
特征值的处理:
a = eig637_value,eig637_vector=np.linalg.eig(corr6_3_7)#特征值计算
#print(a)
eig6_3_7=pd.DataFrame({"eig637_value":eig637_value})
eig6_3_7=eig6_3_7.sort_values(by=["eig637_value"], ascending=False) #特征值进行排序
print(eig6_3_7)
# eig637_value
#0 6.593491e+00
#1 6.496108e-01
#2 4.224150e-01
#3 2.012979e-01
#4 7.705858e-02
#5 3.650975e-02
#6 1.961697e-02
#7 -1.568963e-16
合并:
eig6_3_7["eig637_cum"] = (eig6_3_7["eig637_value"]/eig6_3_7["eig637_value"].sum()).cumsum()#获取累积贡献度
#print(eig6_3_7)
eig6_3_7=eig6_3_7.merge(pd.DataFrame(eig637_vector).T, left_index=True, right_index=True)#将特征值合并
print(eig6_3_7)
# eig637_value eig637_cum 0 ... 5 6 7
#0 6.593491e+00 0.824186 0.373021 ... -0.331959 -0.343716 -0.279402
#1 6.496108e-01 0.905388 0.124127 ... 0.252365 0.300737 -0.839027
#2 4.224150e-01 0.958190 0.213199 ... 0.704605 -0.608927 0.116163
#3 2.012979e-01 0.983352 -0.366087 ... 0.305323 -0.119075 -0.330367
#4 7.705858e-02 0.992984 -0.351342 ... -0.184792 -0.053431 -0.053209
#5 3.650975e-02 0.997548 0.621083 ... 0.032407 0.238409 0.036365
#6 1.961697e-02 1.000000 -0.375707 ... 0.213750 0.161151 0.042581
#7 -1.568963e-16 1.000000 0.125033 ... 0.394383 0.566376 0.298941
可视化:
#####################绘图
plt.scatter(range(1, DF6_3_7.shape[1] + 1), eig637_value)
plt.plot(range(1, DF6_3_7.shape[1] + 1), eig637_value)
plt.title("Scree Plot")
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")
plt.grid() # 显示网格
plt.show() # 显示图形
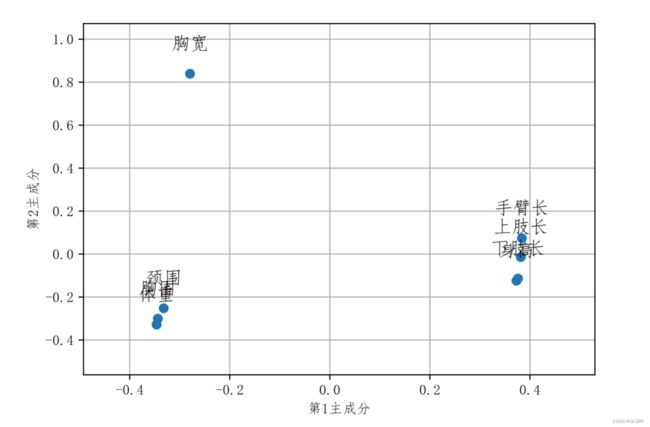
df637_std = (DF6_3_7 - DF6_3_7.mean())/DF6_3_7.std()#成分得分系数矩阵(因子载荷矩阵法)
loading = eig6_3_7.iloc[:2,2:].T
loading["vars"]=df637_std.columns
loading
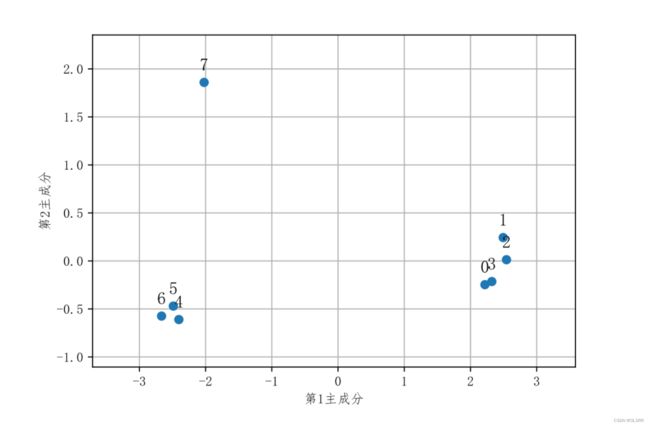
#计算得分
score = pd.DataFrame(np.dot(df637_std,loading.iloc[:,0:2]))
print(score)
# 0 1
#0 2.217923 0.247088
#1 2.493903 -0.243507
#2 2.543724 -0.012974
#3 2.322092 0.214425
#4 -2.403791 0.610378
#5 -2.487041 0.469943
#6 -2.664640 0.574143
#7 -2.022170 -1.859498
可以认为,第一主成分是对身高的度量,第二主成分是对手臂长的度量,第三主成分很难给出明显的解释,因此只取前两个主成分。
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus'] = False
plt.plot(loading[0],loading[1], "o")
xmin ,xmax = loading[0].min(), loading[0].max()
ymin, ymax = loading[1].min(), loading[1].max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xlabel('第 1 主成分')
plt.ylabel('第 2 主成分')
for x, y,z in zip(loading[0], loading[1], loading["vars"]):
plt.text(x, y+0.1, z, ha='center', va='bottom', fontsize=13)#影响力与正负数无关,只看绝对值。
plt.grid(True)
plt.show()
plt.plot(score[0],score[1], "o")
xmin ,xmax = score[0].min(), score[0].max()
ymin, ymax = score[1].min(), score[1].max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xlabel('第 1 主成分')
plt.ylabel('第 2 主成分')
for x, y,z in zip(score[0], score[1], score.index):
plt.text(x, y+0.1, z, ha='center', va='bottom', fontsize=13)
plt.grid(True)
plt.show()
# (-3.7063124402737815, 3.5853963242935594)
# (-1.1043536884564529, 2.353473153176396)