Python 中的主成分分析 (PCA)

无监督学习

什么是主成分分析

当我们执行主成分分析 (PCA) 时，我们希望找到数据集的主成分。令人惊讶不是吗？那么，数据集的主要组成部分是什么，我们为什么要找到它们，它们告诉我们什么？数据集的主成分是数据集中变化最大的“方向”（我假设您对术语方差有基本的了解。如果没有，请在此处查找。简单来说，第一个主成分是数据集是沿数据集变化最大的方向。

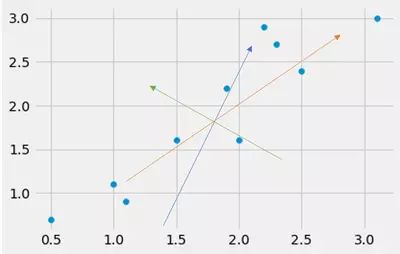
考虑以下数据集，我在其上绘制了由不同颜色箭头表示的不同“方向”。你怎么看，哪个箭头指向数据集方差最大的方向？

好吧，通过肉眼我们看到橙色箭头可能指向方差最大的方向。

好的，但是为什么我们需要这个方向？

我们希望有这个方向（方差最大的方向），因为将来我们希望使用数据集的主成分来降低数据集的维度，或者通过将其减少到三个或更少的维度来使其“可绘制”，或者只是在不丢失太多信息的情况下减小数据集的大小。降低数据集的维度就像通过组合列来创建新列，使得新==组合的列数小于原始列数。

想象一个只有两列 A 和 B 的数据集，那么这个数据集就被称为是二维的。如果我们现在将这两列合并为一列，例如通过简单地添加第一列和第二列，数据集就会减少到一维。决定应该组合哪些列以及我们应该如何组合它们是 PCA 的目标。请注意，此插图并非 100% 正确，因为 PCA 的目标是转换数据，而不是简单地切掉或组合某些内容，而是此插图应该对它进行第一步。

也就是说，我们希望减小数据集的大小以使算法更容易使用，或者通过将数据变为 2 维或 3 维来简单地可视化数据。

但是等等，我说减小数据集的大小，这有点“丢失一些东西”，对吗？正确的！通过减少数据集的维数，我们会松散维度，即我们会松散信息。想象一个 3D 电影，我们移除了第三维，使得剩下的电影是二维的。我们仍然可以观看电影，但我们丢失了一些信息。我们必须找到答案的问题是：哪些维度包含数据集的最多信息，哪些维​​度只包含很少信息——因此可以在不丢失太多信息的情况下被截断。

找到这些维度（主成分）并使用这些主成分将数据集转换为较低维度的数据集是 PCA 的任务。如上所述，最后我们使用找到并选择的主成分来转换我们的数据集，即使用这些主成分来投影我们的数据集（投影是通过矩阵乘法完成的）。通过这样做，我们得到了一个维度减少（即减小的大小）的数据集，而不会丢失太多信息——希望如此——。

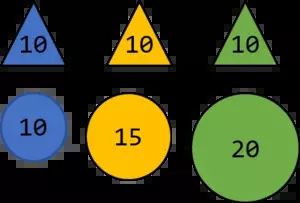
好的，要继续，为了理解，我们必须退后一小步。我们想要找到主成分，因为这些是具有最高方差的数据集的“方向”。你问自己：为什么方差最大？好吧，事实证明具有最高方差（主成分）的方向是信息量最大的方向。让我们用一个小图形说明清楚这一点：

由于分配给三角形的值（假设单位为 kg）都相同，因此方差为 0，而球的方差为 16.66  克G2

现在让我们进一步假设有人选择了一个球和一个三角形，告诉您分配的权重，并希望您对颜色进行预测。无论人选择什么三角形，重量总是 10 公斤，因此你没有机会根据公斤数正确预测三角形的颜色。但是，球的重量不同（它们的方差比三角形更大），无论人们告诉您什么重量，您都可以根据数字预测颜色。为了更清楚地说明这一点，假设在下一步中，此人希望您做同样的事情，但现在他或她没有告诉您确切的数字，而只是告诉您一个接近上述数字之一的数字。例如，11公斤。

根据这个数字，你可以预测球的颜色为蓝色，因为 11 比 15 更接近 10。因此，分配的权重越远，即方差越大，你就越容易预测颜色。请把上述作为主要思想，为什么我们可以使用方差作为信息量的衡量标准，而不是声称 100% 的数学正确性。

好的，现在我们已经明白为什么我们想要具有最高方差（主成分）的方向。但在我们的路上，主要问题仍未得到解答。*我们如何获得这些主成分？* 我们通过找到具有最高方差的方向来获得这些主成分。

聪明的家伙……我们已经知道了。这句话包含两个重要的词：方向和方差——找到*方差*最高的*方向*——。好吧，我们可以做和我上面做的完全一样的事情，只需在数据集中画一条任意线。要知道这条线的好坏，我们必须沿着这条线测量数据的方差。现在我们知道（总体的）方差的公式是：

v一个r(X)=∑一世=1n(X一世-X¯)2n

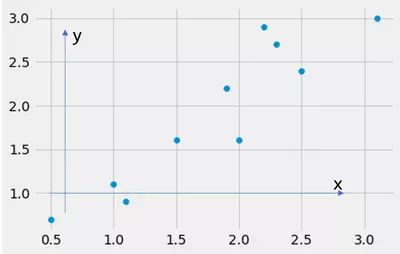
但是这里 x 是一维的，我们的数据集有两个维度 x 和 y，因此：我们应该使用它们中的哪一个作为 X在方差计算中？我们应该计算 x 或 y 的方差吗？答案是：没有一个是正确的。为什么？看下图：

在这张图中，我画了两个箭头，一个指向 x 轴的方向，一个指向 y 轴的方向。如果我沿着这些箭头计算方差会发生什么？好吧，我计算沿特征 x 和沿特征 y 的方差。数据集如下所示：

import  pandas  as  pd 
import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
style 。使用( "fivethirtyeight" )
将 numpy 导入为 np


数据 =  np 。阵列（[[ 2.5 ，0.5 ，2.2 ，1.9 ，3.1 ，2.3 ，2 ，1 ，1.5 ，1.1 ]，[ 2.4 ，0.7 ，2.9 ，2.2 ，3.0 ，2.7 ，1.6 ，1.1 ，1.6 ，0.9 ]]）
打印（数据）
无花果 =  plt 。图()
ax0  = 图。add_subplot ( 111 )

轴0 。分散（数据[ 0 ]，数据[ 1 ]）

PLT 。显示()

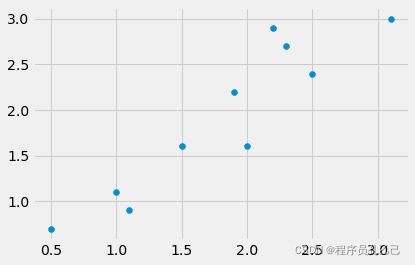
输出：  

[[2.5 0.5 2.2 1.9 3.1 2.3 2. 1. 1.5 1.1] [2.4 0.7 2.9 2.2 3. 2.7 1.6 1.1 1.6 0.9]]

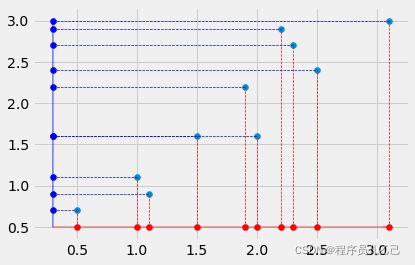
其中第一个列表表示 x 特征，第二个列表表示 y 特征。考虑下面的代码。如果我们沿着*x-箭头* 和*y-箭头* 计算数据集的方差会发生什么？我们计算沿特征 x 和 y 的方差！我们通过分别忽略另一个维度（特征）x 或 y 来隐式地做到这一点。也就是说，通过忽略 x 或 y，我们将数据投影到 x 或 y 轴上，从而降低维度，即切掉一维。

import  pandas  as  pd 
import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
style 。使用( "fivethirtyeight" )
将 numpy 导入为 np


数据 =  np 。阵列（[[ 2.5 ，0.5 ，2.2 ，1.9 ，3.1 ，2.3 ，2 ，1 ，1.5 ，1.1 ]，[ 2.4 ，0.7 ，2.9 ，2.2 ，3.0 ，2.7 ，1.6 ，1.1 ，1.6 ，0.9 ]]）
打印（数据）
无花果 =  plt 。图()
ax0  = 图。add_subplot ( 111 )

轴0 。分散（数据[ 0 ]，数据[ 1 ]）
ax0 。散射（数据[ 0 ]，NP 。ones_like （数据[ 1 ]）*分钟（数据[ 1 ]）- 0.2 ，颜色= “红” ）
AX0 。散射（NP 。ones_like （数据[ 0 ]）*min ( data [ 0 ]) - 0.2 , data [ 1 ], color = "blue" ) 
ax0 。箭头( min ( data [ 0 ]) - 0.2 , min ( data [ 1 ]) - 0.2 , 0 , max ( data [ 1 ]) - 0.5 , width = 0.01 , color ="blue" , alpha = 0.4 , length_includes_head = "True" ) 
ax0 。箭头( min ( data [ 0 ]) - 0.2 , min ( data [ 1 ]) - 0.2 , max ( data [ 0 ]) - 0.3 , 0 , width = 0.01 , color = "red" , alpha = 0.4 ,length_includes_head = "True" ) 
ax0 。vlines ( data [ 0 ], min ( data [ 1 ]) - 0.2 , data [ 1 ], colors = "red" , linestyles = "--" , linewidth = 0.7 ) 
ax0 。hlines ( data [ 1 ], min ( data [ 0 ]) - 0.2 ,数据[ 0 ]，颜色= “蓝色” ，线型= “--” ，线宽= 0.7 ）


PLT 。显示()

输出：  

[[2.5 0.5 2.2 1.9 3.1 2.3 2. 1. 1.5 1.1] [2.4 0.7 2.9 2.2 3. 2.7 1.6 1.1 1.6 0.9]]

现在您可以看到选择 x 和 y 轴作为我们的主要组件的效果。我们将数据投影到 x 和 y 轴上。我们现在可以计算投影数据的方差，看看我们的好坏。如果您对我们如何完成这种转变感到困惑，请保持冷静，我们稍后再讨论。

所以现在我们选择了 x 和 y 轴作为我们的主要组件。但如上所述，在这种情况下，这很可能是不正确的，因为我们已经看到从左下角到右上角的倾斜（绿色）线是向量跨越的线，指向最高变化的方向 == 1 . 主成分（在这一点上我不得不提到，一个数据集的主成分与其维度一样多，但第一个主成分是“最强的”）。所以我们首先假设，这条倾斜的绿线实际上是数据集的第一个主成分，即指向最大变化方向的向量。如果我们选择任意向量并做与我们将 x 和 y 方向作为我们假设的主成分完全相同的事情，这看起来如何（请注意，我们想要将数据投影到线上，因为我们想要计算变化）。请注意，由于我们现在进行实际计算，因此必须将数据归一化为零均值，否则计算将失败。

我们现在将绘制数据集并选择可以使用滑块更改其值的任意向量。我们将数据集投影到向量跨越的线上（由滑块值定义）。我们使用选择的向量转换数据集并计算结果方差。导致最大方差的点（滑块调整）为我们提供了第一个主成分。此外，我们根据我们为向量选择的值绘制“方差曲面”。总而言之，通过改变线的方向，我们希望找到这条线，当数据集投影到这条线上时，这条线会导致最大的方差。这条线是 1. 主成分。如果我们选择平行于 x 和 y 轴的线，我们只需切断另一个轴。

import  numpy  as  np 
import  pandas  as  pd 
from  ipywidgets  import  interact 、interactive 、fixed 、interact_manual 
import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
from  mpl_toolkits.mplot3d  import  Axes3D 
style 。使用（'五三十八' ）


定义 f ( x , y ):
    
    数据 =  np 。阵列（[[ 2.5 ，0.5 ，2.2 ，1.9 ，3.1 ，2.3 ，2 ，1 ，1.5 ，1.1 ]，[ 2.4 ，0.7 ，2.9 ，2.2 ，3.0 ，2.7 ，1.6 ，1.1 ，1.6 ，0.9 ]）
    的数据[ 0 ]  = 数据[ 0 ] - np. 均值（数据[ 0 ]）
    数据[ 1 ]  = 数据[ 1 ] - np 。平均值（数据[ 1 ]）
 
    # 创建轴

    无花果 =  plt 。图( figsize = ( 10 , 10 )) 
    ax0  =  fig . add_subplot ( 121 ) 
    ax0 。set_aspect ( 'equal' ) 
    ax0 。set_ylim ( - 2 , 2 ) 
    ax0 。set_xlim ( - 2 , 2 ) 
    ax0 。set_title ( '搜索主成分' , fontsize =14 ) 
    ax0 。set_xlabel ( 'PC x value' , fontsize = 10 ) 
    ax0 。set_ylabel ( 'PC y 值' , fontsize = 10 )
    



    #vec = np.array([0.6778734,0.73517866]) 
    vec  =  np . 数组([ x , y ])

    轴0 。分散（数据[ 0 ]，数据[ 1 ]）
    ax0 。情节（NP 。linspace （分钟（数据[ 0 ]），最大（数据[ 0 ]）），（VEC [ 1 ] / VEC [ 0 ]）* NP 。linspace （分钟（数据[ 0 ]），最大（数据[0 ])), linewidth = 1.5 , color = "black" , linestyle = "--" )



    b_on_vec_list  =  [[],[]] 
    for  i  in  range ( len ( data [ 0 ])): 
        a  =  vec 
        b  =  np 。数组([ data [ 0 ][ i ], data [ 1 ][ i ]]) 
        b_on_a  =  ( np . dot ( a , b ) / np . dot ( a , a )) *a 
        b_on_vec_list [ 0 ] 。追加( b_on_a [ 0 ]) 
        b_on_vec_list [ 1 ] 。追加( b_on_a [ 1 ]) 
        ax0 。分散( b_on_a [ 0 ], b_on_a [ 1 ], color = 'red' ) 
        ax0 。绘图([ b_on_a [ 0 ], b [ 0 ]],[ b_on_a [ 1], b [ 1 ]], "r--" , linewidth = 1 )


    ax1  = 图。add_subplot ( 122 ,投影= '3d' ) 
    ax1 。set_aspect ( 'equal' ) 
    ax1 。set_ylim ( 0 , 1 ) 
    ax1 。set_xlim ( 0 , 1 ) 
    ax1 。set_title ( 'Varicane 相对于 1. PC' , fontsize = 14 ) 
    ax1 . set_xlabel ( 'PC x value' , fontsize= 10 ) 
    ax1 。set_ylabel ( 'PC y value' , fontsize = 10 ) 
    ax1 。set_zlabel （'方差' ，fontsize = 10 ）

    

    ＃变换数据
    e_vec  =  （1 / NP 。SQRT （NP 。点（VEC ，VEC 。Ť ）））* VEC 
    data_trans  =  NP 。点（数据。Ť ，e_vec ）
    
    # 绘制数据
    ax0 。scatter ( data_trans , np . zeros_like ( data_trans ), c = 'None' , edgecolor = 'black' ) 
    # 绘制扭曲线
    ax0 。情节（NP 。linspace （分钟（data_trans ），最大值（data_trans ），10 ），NP 。zeros_like （data_trans ），线型= ' - '，颜色= '灰色' ，线宽= 1.5 ）
    ＃剧情圆圈
    为 我 在 范围（len个（data_trans ））：
        AX0 。add_artist ( plt . Circle (( 0 , 0 ), data_trans [ i ], linewidth = 0.5 , linestyle = 'dashed' , color = 'grey' , fill = False ))

    # 计算方差    
    ax0 。文本（0 ，- 1.4 ，'方差= {0} ' 。格式（STR （NP 。圆（NP 。VAR （data_trans ），3 ））），字体大小= 20 ）


    # 绘制关于主成分向量的方差

    # 初始化网格
    cross_x , cross_y  = np . meshgrid （NP 。linspace （0.001 ，1 ，NUM = 20 ），NP 。linspace （0.001 ，1 ，NUM = 20 ）） 
    ＃格式为[（0.01,0.01）创建迭代器，（0.01,0.0620），（0.01 ，0.114），...（0.0620,0.01），（0.0620,0.0620），（0.0620,0.1141），...（0.999,0.01），（0.999,0.0620），...（0.999,0.999）] 
    x_y_pairs  =  []
    为 我 在 范围（len ( cross_y )): 
        x_y_pairs 。append ( list ( zip ( cross_x [ i ], cross_y [ i ]))) 
    flatten_x_y_pairs  =  [ np . 数组（列表（x_y ）） 用于x_y_pairs中的子列表，用于 子列表 中的 x_y  ]   


    方差 =  [] 
    for  i  in  flatten_x_y_pairs ：
        e_vec  =  ( 1 / np . sqrt ( np . dot ( i , i . T ))) * i 
        data_trans  =  np . 点（数据。Ť ，e_vec 。Ť ）
        方差。追加（NP 。VAR （data_trans ））

    
        
    index_of_max_variance  =  np 。where ( variances  ==  max ( variances ))[ 0 ][ 0 ] 
    #PLot 方差表面
    ax1 。散射（cross_x ，cross_y ，NP 。阵列（方差）。重塑（20 ，20 ），阿尔法= 0.8 ）


    # 标记方差
    最大 的点vec_point =  np . 阵列（[ X ，ÿ ]）
    e_vec_point  =  （1 / NP 。SQRT （NP 。点（vec_point ，vec_point 。Ť ）））* vec_point 
    data_trans_point  =  NP 。点（数据。Ť ，e_vec_point 。Ť ）
    AX1 。散射( x, y , np 。var ( data_trans_point ) + 0.01 , color = "orange" , s = 100 )
    
    
    
    

    PLT 。显示()
    
    
交互( f , x = ( 0.001 , 1 , 0.001 ), y = ( 0.001 , 1 , 0.001 ))

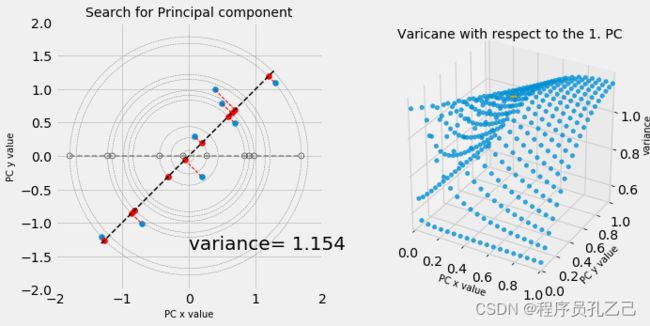
输出：  

<函数 __main__.f(x, y)>

通过使用滑块，我们可以看到 [0.67,0.73] 的滑块值导致最高方差。还要注意灰色虚线圆圈以及 x 轴上的灰色散点。如果我们将数据集投影到所选向量所跨越的线上，并围绕这条线进行某种扭曲，使其与我们原来的 x 轴对齐，我们将跨越线作为我们的新 x 轴。在改变向量值的同时，我们现在可以观察这些值在 x 轴上的分布，这些值分布得越多，方差就越大。数据集的这种投影和跨线的扭曲是通过使用所选向量转换原始数据集来完成的。

但是等等，你说投影和转换......我们如何投影数据？好吧，因此您必须熟悉线性代数。如果你是，那很好。如果没有，这个关于线性代数本质的youtube 播放列表可能非常有用。所以我们正在做的只是计算我们的数据集和所选向量的 *点积 *（有时也称为标量积）。现在为简单起见，假设我们使用任意数据集并希望将此数据集投影到 y 轴上。要投影数据集，我们需要两件事。一、shape的数据集nXn 和一个形状向量 nX米. 我们知道，计算点积后，得到的数据集具有维数nX米 因此如果 米

假设我们有一个 10X2数据集，我们希望将此数据集投影到指向 y 轴方向的向量所跨越的线上（这与我们上面所做的相同）。这个向量是单位向量 [0,1]，它有维数1X2. 我们想要的是投影到 y 轴上的数据集，以及具有维度的数据集10X1. 因此，要实现这一点，我们必须计算以下项的点积：

d一个吨一个＊v电子C吨 在哪里 v电子C吨 是转置的单位向量，因此不再具有形状 1X2 但 2X1 并且由此产生的数据集具有形状 10X1. 如果我们现在在实践中进行所描述的计算，这看起来像：

将 numpy 导入为 np 
data  =  np 。阵列（[[ 2.5 ，0.5 ，2.2 ，1.9 ，3.1 ，2.3 ，2 ，1 ，1.5 ，1.1 ]，[ 2.4 ，0.7 ，2.9 ，2.2 ，3.0 ，2.7 ，1.6 ，1.1 ，1.6 ，0.9 ]]）
EX  =  NP . 数组([[1 , 0 ]]) 
ey  =  np 。数组([[ 0 , 1 ]])

打印（数据。形状）
打印（EX 。形状）

print ( np . dot ( data . T , ey . T ))  # 如您所见，这正是我们数据集的 y 分量（x 维）

输出：

(2, 10)
(1, 2)
[[2.4]
 [0.7]
 [2.9]
 [2.2]
 [3. ]
 [2.7]
 [1.6]
 [1.1]
 [1.6]
 [0.9]]

如您所见，结果与原始数据集的 y 值相同。这是合乎逻辑的，因为通过将数据转换到 y 轴（看上面的图）我们只是省略了数据集的 x 值。现在假设我们不使用向量 [0,1]，它是指向 y 轴方向的单位向量，而是使用任何其他任意向量，例如 [0.653,1.2] 会发生什么？好吧，计算完全相同：我们计算 10x2 数据集与 2x1 向量的点积，并得到维度为 10x1 的数据集投影到该向量上。尽管如此，我们将数据投影到的线不再是一条垂直线，而是一条斜率为 1.2/0.653 的斜线。

import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
style 。使用( 'fivethirtyeight' ) 
import  numpy  as  np 
import  matplotlib.patches 作为 补丁

def  f （羊肉）：

    # 单位向量
    e_x  =  np . 数组([ 1 , 0 ]) 
    e_y  =  np 。数组([ 0 , 1 ])


    ＃区跨越由单位矢量
    打印（NP 。交叉（e_x ，E_Y ））  ＃区跨越由单位矢量== 1


    # 任何形状为 (A-lambda*I) 
    A  =  np 的二维矩阵 A 。数组([[ 2 -羔羊, 3 ],[ 3 , 0.5 -羔羊]])



    # 用矩阵 A 变换单位向量 --> 不出所料，这正是矩阵 A，否则
    “行列式描述变换后单位向量所跨越的区域的变化”的符号是没有意义的

    # 绘制向量
    fig  =  plt . 图( figsize = ( 10 , 10 )) 
    ax0  =  fig . add_subplot ( 111 ) 
    ax0 。set_xlim ( - 5 , 8 ) 
    ax0 。set_ylim ( - 5 , 8 ) 
    ax0 。set_aspect ( '相等' )

    # 矩阵 A 
    ax0 的向量。arrow ( 0 , 0 , A [ 0 ][ 0 ], A [ 0 ][ 1 ], color = "red" , linewidth = 1 , head_width = 0.05 )  #第一个向量
    ax0 。箭头( 0 , 0 , A [ 1 ][ 0 ], A [ 1 ][ 1 ],颜色= "blue" , linewidth = 1 , head_width = 0.05 )  # 第二个向量



    # 向量跨越的区域** 
    ax0 。箭头( A [ 0 ][ 0 ], A [ 0 ][ 1 ], A [ 1 ][ 0 ], A [ 1 ][ 1 ], color = "blue" , linestyle = 'dashed' , alpha = 0.3 ,线宽= 1 , head_width = 0.05 ) 
    ax0 。箭头( A[ 1 ][ 0 ], A [ 1 ][ 1 ], A [ 0 ][ 0 ], A [ 0 ][ 1 ], color = "red" , linestyle = 'dashed' , alpha = 0.3 , linewidth = 1 , head_width = 0.05 ) 
    ax0 。add_patch (补丁。多边形( xy = [[ 0, 0 ],[ A [ 0 ][ 0 ], A [ 0 ][ 1 ]],[ A [ 0 ][ 0 ] + A [ 1 ][ 0 ], A [ 0 ][ 1 ] + A [ 1 ][ 1 ]],[ A [ 1 ][ 0 ], A [ 1 ][ 1 ]]], fill = True , alpha =0.1 ,颜色= '黄色' ))
    
    # 添加显示行列式和面积
    ax0计算的文本。文本（3 ，- 0 ，小号= - [R '$行列式= A_ {11} * A_ {22} -a_ {21} * A_ {12} $' + '= {0} ' 。格式（NP 。轮（甲[ 0 ][ 0 ] * A [ 1 ][ 1 ] - A [ 1 ][ 0] * A [ 0 ][ 1 ], 3 ))) 
    #ax0.text(3,-1,s='area = {0}'.format(np.round(np.cross(AT[0],AT) [1]),3))) 
    ax0 。文本( 3 , - 0.5 , s = r '$determinant$' + '= {0} * {1} - {2} * {3} = {4} ' .格式( A [ 0 ][ 0 ], A [ 1 ][ 1 ], A[ 1 ][ 0 ]，A [ 0 ][ 1 ]，np 。round ( A [ 0 ][ 0 ] * A [ 1 ][ 1 ] - A [ 1 ][ 0 ] * A [ 0 ][ 1 ], 3 ))) 
    ax0 。text ( 3 , - 4 , s = '**注意在这种情况下行列式的值\n和 area(cross product --> Yellow shaded) 是相同的\n因为单位向量跨越的区域是 1' ，fontsize = 8 )
    
    
    # 绘制特征向量
    ax0 。箭头( 0 , 0 , 0.61505 , - 0.788491 , color = "black" , linestyle = 'dashed' , alpha = 0.3 , linewidth = 1 , head_width = 0.05 ) 
    ax0 。箭头( 0 , 0 , 0.78771 , 0.6159 , color = "black" , linestyle ='dashed' , alpha = 0.3 , linewidth = 1 , head_width = 0.05 )
    
    # 使用找到的特征向量为不同的 lambda 值计算 (A-lambda I)*nu。
    当 nu 垂直于 (A-lambda I) 时
    ，结果必须为# 0 # 注意，对于 v1 和 v2 的计算，我们必须求解线性方程组 (A-lambda I)*v=0 
    # 对于 v1 和v2   
    
    v1  =  - 3 * ((( - 1 + 0.5 *羊肉) / ( - 9 - 2 *羊肉+羊肉** 2 ))) / ( 2 -羊肉) 
    v2  =  ( - 1 + 0.5 *羊肉) / ( - 9 - 2 *羊肉+羊肉** 2 ) 
    v  =  np .阵列（（1 / NP 。SQRT （V1 ** 2 + V2 ** 2 ））* NP 。阵列（[ V1 ，V2 ））
    AX0 。text ( 3 , - 1 , s = r '$(A-$' + ' {0} ' . format ( lamb ) + r '$I)*\nu$' + '= {0} ' . format( np . round ( np . dot ( A , v ), 3 ))) 
    ax0 . 箭头( 0 , 0 , - v [ 0 ] * 0.5 , - v [ 1 ] * 0.5 , color = "green" , alpha = 0.8 , linewidth = 1 , head_width = 0.05 ) # 我们为 lambda 绘制特征向量
                                                                                        # Mind v[0]*0.5 和 v[1]*0.5 --> *0.5 
                                                                                        # 仅用于可视化目的
    
   
    
    
    
    
    PLT 。显示()
    
互动( f ,羔羊= ( - 5 , 5 , 0.001 ))
 

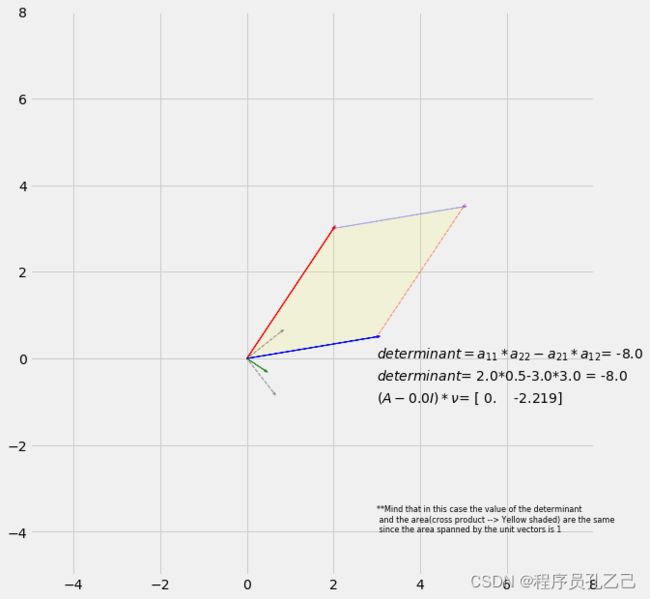
输出：  

1

上面我们运行了步骤 1 到 4，所以接下来是使用特征向量转换数据。

电阻电子d你C电子  吨H电子  d一世米电子n秒一世○n一个升一世吨是  ○F  吨H电子  d一个吨一个  -  磷你吨吨一世nG  一个升升  吨○G电子吨H电子r―

一旦我们找到了数据集的特征向量和特征值，我们最终可以使用这些向量（它们是数据集的主成分）来降低数据的维数，即将数据投影到主成分上。

因此，让我们这样做，同时执行上述所有步骤，以展示在我们使用预先打包的 sklearn PCA 方法之前，如何使用 Python 从头开始​​使用 PCA 来完成降维。为了说明这一点，我们将使用 UCI Iris 数据集。

import  numpy  as  np 
from  sklearn.preprocessing  import  StandardScaler 
from  sklearn.cross_validation  import  train_test_split 
import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
style 。使用( 'fivethirtyeight' )
导入 熊猫 作为 pd


"""1. 收集数据"""

df  =  pd 。read_table ( 'data\Wine.txt' , sep = ',' , names = [ '酒精' , '苹果酸' , '灰分' , '灰分碱度' , '镁' , '总酚' , 
                                                 '类黄酮' , 'Nonflavanoid_phenols' 、'原花青素' 、'Color_intensity' 、'Hue' 、
                                                 'OD280/OD315_of_diluted_wines' 、'脯氨酸' ]）

目标 =  df 。指数


"""2. 规范化数据""" 


df  =  StandardScaler () 。fit_transform ( df )



"""3.计算协方差矩阵"""        

COV  =  np 。cov ( df . T )  # 自 np.cov() sais 的文档以来，我们必须转置数据
                   # `m` 的每一行代表一个变量，每列代表一个变量
                   # 所有这些变量的观察


"""4.求协方差矩阵的特征值和特征向量""" 

eigval , eigvec  =  np 。linalg 。EIG （COV ）
打印（NP 。cumsum （[我* （100 /总和（eigval ）） 为 我 在 eigval ]））  ＃正如可以看到的，前两个主成分含有的55％ 
                                                        ＃而第一总变异8 PC 含 90%



"""5.使用主成分对数据进行变换——降低数据的维数"""

# wine 数据集是 13 维的，我们想将维数减少到 2 维
# 因此我们使用具有两个最大特征值的两个特征向量，并使用这个向量
# 对原始数据集进行变换。
# 我们想要 2 维因此结果数据集应该是一个 178x2 的矩阵。
# 原始数据集是一个 178x13 矩阵，因此“主成分矩阵”必须是
# 形状 13*2，其中 2 列包含具有两个最大特征值的协方差特征向量

PC  =  eigvec 。T [ 0 : 2 ]



data_transformed  =  np . dot ( df , PC . T )  # 我们必须转置 PC 因为它的格式是 2x178


# 绘制数据

无花果 =  plt 。图( figsize = ( 10 , 10 )) 
ax0  =  fig . add_subplot ( 111 )


轴0 。scatter ( data_transformed . T [ 0 ], data_transformed . T [ 1 ]) 
for  l , c  in  zip (( np . unique ( target )),[ 'red' , 'green' , 'blue' ]): 
    ax0 . 分散( data_transformed . T [ 0 , target == l ], data_transformed . T[ 1 ,目标== l ], c = c ,标签= l )

轴0 。传说()



PLT 。显示()

输出：

-------------------------------------------------- ------------------------- 
ModuleNotFoundError                        Traceback (最近一次调用最后一次)
  in  
      1  import numpy as来自sklearn 的np
       2  。预处理导入StandardScaler
 ----> 3 from sklearn 。cross_validation导入train_test_split
       4导入matplotlib 。pyplot作为来自matplotlib 的plt
       5   进口风格

ModuleNotFoundError : 没有名为“sklearn.cross_validation”的模块

如您所见，13 维数据集已缩减为 2 维数据集，该数据集仍占总变异的 55%，我们现在可以将其绘制到二维坐标系中。请注意，通常我们没有数据集的目标特征值，因为 PCA 是一种无监督学习算法。尽管如此，我们在这里包含了目标特征值，以表明数据集仍然可以很好地分离，只有二维。所以我们上面所做的是，通过使用数据集的主成分转换数据集，我们已经从其他特征中创建了新特征，从而降低了数据集的维数（我们转换后的数据集的其余列作为新特征） ) 不会丢失太多信息。

上面的代码比手动搜索主成分要短得多，也方便得多。接下来，我们将（一如既往）使用预先打包的 sklearn PCA使其更加高效。

使用 sklearn 的 PCA

from  sklearn.decomposition  import  PCA 
import  numpy  as  np 
from  sklearn.preprocessing  import  StandardScaler 
from  sklearn.cross_validation  import  train_test_split 
import  matplotlib.pyplot  as  plt 
from  matplotlib  import  style 
style 。使用( 'fivethirtyeight' )
导入 熊猫 作为 pd


"""1. 收集数据"""

df1  =  pd 。read_table ( 'data\Wine.txt' , sep = ',' , names = [ '酒精' , '苹果酸' , '灰分' , '灰分碱度' , '镁' , '总酚' , 
                                                 '类黄酮' , 'Nonflavanoid_phenols' 、'原花青素' 、'Color_intensity' 、'Hue' 、
                                                 'OD280/OD315_of_diluted_wines' 、'脯氨酸' ]）

目标 1  =  df1 。指数


"""2. 规范化数据""" 


df1  =  StandardScaler () 。fit_transform ( df )


"""3.使用PCA并降低维数"""

PCA_model  =  PCA ( n_components = 2 , random_state = 42 )  # 我们将维数减少到二维并将
                                                            # 随机状态
设置为 42 data_transformed  =  PCA_model 。fit_transform ( df1 , target ) * ( - 1 )  # 如果我们省略 -1 我们得到完全相同的结果，但旋转了 180 度 --> y 轴上的 -1 变为 1。
                                                            # 这是由于定义向量。我们可以将向量 a 定义为 [-1,-1] 和 [1,1]
                                                            # 跨越的行是相同的 --> 删除 *(-1) 你会看到

# 绘制数据

无花果 =  plt 。图( figsize = ( 10 , 10 )) 
ax0  =  fig . add_subplot ( 111 )


轴0 。scatter ( data_transformed . T [ 0 ], data_transformed . T [ 1 ]) 
for  l , c  in  zip (( np . unique ( target )),[ 'red' , 'green' , 'blue' ]): 
    ax0 . 分散( data_transformed . T [ 0 , target == l ], data_transformed . T[ 1 ,目标== l ], c = c ,标签= l )

轴0 。传说()



PLT 。显示()

如您所见，我们实际上只需要几行代码即可完成 PCA。一旦您了解了 PCA 背后的思想，您就可以使用这种非常方便的预先打包的 sklearn 方法，而无需担心降低数据集的维数以使其成为 *plottable* 或在不丢失太多编码信息的情况下减小数据集的大小. 阅读文档以了解如何使用此函数的属性。例如，您可以打印特征空间中的主轴以及每个选定组件的解释方差。随便玩玩吧 恭喜，如果您可以按照上述所有步骤进行操作，那么您已经了解了一种更复杂的机器学习算法。完毕！

参考

• 线性组合、跨度和基向量 | 第 2 章，线性代数的本质 （Youtube）
• 主成分分析（PCA）解释清楚 （Youtube）
• 理解主成分分析特征向量特征值 (StackExchange)
• 线性代数的本质 （Youtube）
• 史密斯，李 (2002)。主成分分析教程 [在线]。可在：主要组件。[2018 年 6 月 13 日访问] [警告：PDF]
• Raschka, S. (2015)。Python机器学习。伯明翰：Packt Publishing Ltd，第 127-148 页。
• 帕普拉，L.（2015 年）。Mathematik fuer Ingenieure 和 Naturwissenschaftler Band 2。第 14 版。威斯巴登：Springer Vieweg，第 120-144 页
• 帕普拉，L.（2014 年）。Mathematik fuer Ingenieure 和 Naturwissenschaftler Band 1 . 第 14 版。威斯巴登：Springer Vieweg，第 45-132 页
• 马斯兰，S.（2015 年）。机器学习算法视角。第二版。博卡拉顿：CRC 出版社，第 129-153 页