从熵到相位传递熵,附matlba和python代码
先来一张图,预览一下最近为了整明白相位传递熵所要恶补的知识叭,泪目了:(

好吧,废话不多说,直接开始吧!
一. 熵是什么?
1、香浓熵
2、联合熵、条件熵和互信息
3、传递熵
二、直方图
1、连续随机变量的传递熵
三、相位传递熵
前言
以前每次听到“熵”这个词就很害怕,觉得好高深啊,不敢也不愿意花时间去学习了解,然而最近由于科研和毕业论文的需求,不得不逼自己静下心来系统的去学习了解,熵到底是何方神圣,为什么平常我们听了都要瑟瑟发抖。
一、熵是什么?
1、香浓熵(信息熵)
通过百度百科我们可以了解到:熵的本质是一个系统“内在的混乱程度”。更具体地说是:一个系统中的粒子具有很大的从新排列的可能性,系统具有较高的熵,反之亦然。举个例子:
例如,水有三种状态:固液气,具有不同的熵值。冰中的分子位置固定,是一个稳定的状态,所以冰具有最低的熵值。水中的分子相对可以进行一些移动,所以水具有中间大小的熵值。水蒸气中的分子几乎可以移动到任何地方,所以水蒸气具有最大的熵值。

上面这个例子来自于文章:香农熵,该博主通过一个简单的例子讲了香浓熵公式的由来,我个人认为讲得非常好,也很好理解,建议小白先去看一下这个例子再回来看一下这篇文章。这里我就不展开细说了,直接给出熵的公式:
![]()
log的底为2,这样计算的熵的单位就是bit。
为了更好理解我这里放一个对数函数的图。图中x表示熵公式中的概率P(x),而概率≤1,所以概率越大,对应的负数值越大,取相反数后越小。所以就有,事件发生的概率(事情的确定性)越大,熵值(事情的不确定性)越小;事件发生的概率(事情的确定性)越小,熵值(事情的不确定性)越大。

2、联合熵、条件熵和互信息
1)、联合熵是一集变量之间不确定性的衡量手段。根据熵的概念,不难推出联合熵的公式为:

若X,Y相互独立(注:常数相互独立),则:H(X,Y) = H(X) + H(Y)
2)、条件熵是指在已知随机变量Y发生的条件下,随机变量X的不确定性,反之亦然。
比如:随机变量X表示一个均衡的六面骰子掷出的点数,Y表示X的奇偶性(Y=0,则表示X是偶数,Y=1则表示X是奇数)。
如果知道X=1,则可判断Y=1,失去了Y=0这一信息的可能性;
如果知道Y=0,则可判断X为偶数,失去X为奇数的可能性。
公式为:
![]()
3)、互信息:是指知道随机变量X,对随机变量Y的不确定性的减少程度(或知道Y后X的不确定性的减少程度),公式为:


这三者之间的关系如下图所示。
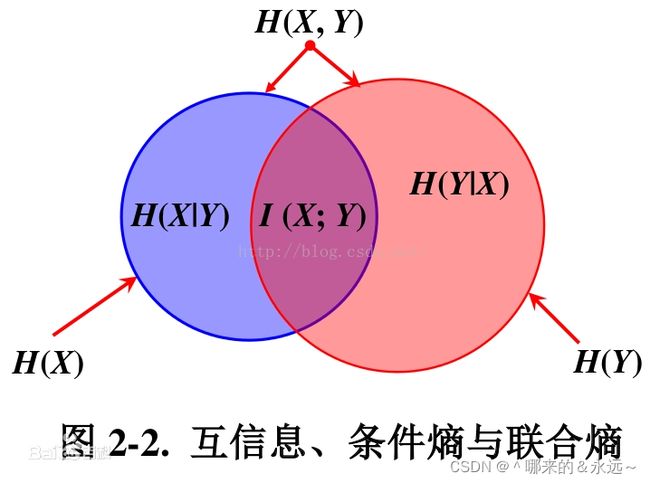
只看公式有点枯燥,下面通过两个小例子去体会一下。
例1:下图为X和Y的联合矩阵,计算

(1)H(Y);

(3)H(Y|X)

例2:血型与皮肤癌的联合概率密度如下表所示,计算I(X;Y)。
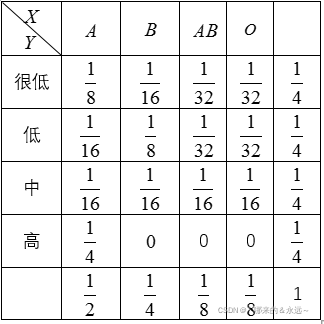

也就是说,知道血型后,知道患癌症的不确定性减少了0.375。互信息的代码可以参见我的另外一篇博客:利用python计算高维标准化互信息并以矩阵形式输出
3、传递熵
关于传递熵的原理,涉及到信息传递之间的因果关系,具体参考:机器学习——建立因果连系(传递熵)这篇是我目前找到的比较通俗的介绍传递熵的文章了。
传递熵原理概括的讲就是:如果知道两个信号(源信号和目标信号)的过去与只知道目标信号的过去相比,能提高预测目标信号未来的信息,则源信号对目标信号有因果影响。在信息论的准则里,从不确定性的角度来理解就是:如果目标信号在其自身的过去和源信号的过去条件下的不确定性小于目标信号在其自身的过去条件下的不确定性,则源信号对目标信号有因果影响。
我这里直接给出公式和韦恩图。
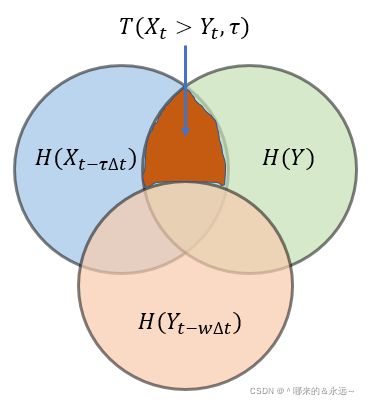
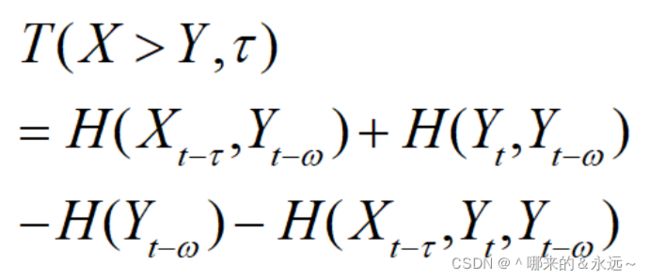
关于传递熵的计算我后面再给出代码,因为上述公式都是只适用于离散信号的,而做脑电信号的知道,其实我们采集到的信号是连续信号,这个时候就涉及到了直方图统计。关于为什么需要直方图,参考这篇文文章:在数据集上计算连续随机变量的信息熵和互信息–k-近邻估计方法。
二、直方图
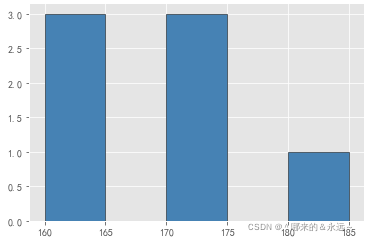
直方图是最简单的非参数密度估计器,也是最常见到的一种。为了构建直方图,我们将数据值所覆盖的区域划分为相等的子区间(bin),每次数据值落入特定的子区间,就将大于等于1的小箱子放在上面。如:选择区间[160,190), binsize=5cm,将7个身高样本数据统计成直方图。

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 让中文能够显示
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['axes.unicode_minus'] = False # 解决负号问题
data = [160,162,183,174,172,161,171]
plt.hist(data,
bins = np.arange(160, 190, 5),
# density = False:那么纵坐标表示落入这个bins的样本个数
# density = True :那么纵坐标表示落入这个bins的样本概率(密度)
density = False,
color='steelblue',
edgecolor='k')
1、连续随机变量的传递熵
matlab代码如下(示例):
clc
clear
%% 加载数据
demo_data1 = [3,5,10,5,9,6,4,3,7,4]';
demo_data2 = [2,4,9,4,8,5,3,2,6,3]';
data = [demo_data1,demo_data2];
L = size(data,1); % number of samples 10
N = size(data,2); % number of signal(channel) 2
TE = zeros(N, N);
%% 计算binsize和delay(这里我是自己设置的,具体是有方法可以根据数据计算的,但我目前还没弄清楚 :))
binsize = 2; % 箱子宽度我设置为2
bins_w = [0:binsize:10]; % 获取各个bin的区间
Nbins = length(bins_w); % 获取bin的个数
delay = 2; % 时间延迟我设置为2
%% 计算TE
for i = 1:N % 遍历各个导联
for j = 1:N
if i~=j
% y and x are past states. ypr is the observed variable.
Py = zeros(Nbins,1); % y 发生的概率
Pypr_y = zeros(Nbins,Nbins); % y and ypr 同时发生的概率
Py_x = zeros(Nbins,Nbins); % y and x 同时发生的概率
Pypr_y_x = zeros(Nbins,Nbins,Nbins); % x、y and ypr 同时发生的概率
% 这里为什么要除binsize,然后(ceil)向上取整呢?目的:计算样本掉进哪个箱子
% 因为本文数据长度是10,如果binsize=2,则有5:[0,2)、(2,4]、(4,6]、(6,8]、(8,10]个箱子。
% 现在有一个样本数据值为8,应该要掉入(6,8]这个箱子,即第4个箱子,所以要让 8/2=4 ( data/binsize = Which box)
rn_ypr = ceil((data(1+delay:end,i)/binsize)); % [5;3;5;3;2;2;4;2]
rn_y = ceil((data(1:end-delay,i)/binsize)); % [2;3;5;3;5;3;2;2]
rn_x = ceil((data(1:end-delay,j)/binsize)); % [1;2;5;2;4;3;2;1]
% 例如 rn_ypr = [5;3;5;3;2;1;4;1] 第1个值为数据值是10的样本要掉进的箱子的序号5
% Py(rn_y(kk))+1 意思为:让 Py矩阵的第5(rn_y(1)=5)个位置+1,即这个箱子现在有一个样本了。
% 二维矩阵亦是如此
% 这时候的直方图的纵坐标表示频数
for kk = 1:(L-delay) % L-delay = 10-2=8
Py(rn_y(kk)) = Py(rn_y(kk))+1; % 计数,即统计每个箱子(bin)的样本个数
Pypr_y(rn_ypr(kk),rn_y(kk)) = Pypr_y(rn_ypr(kk),rn_y(kk))+1;
Py_x(rn_y(kk),rn_x(kk)) = Py_x(rn_y(kk),rn_x(kk))+1;
Pypr_y_x(rn_ypr(kk),rn_y(kk),rn_x(kk)) = Pypr_y_x(rn_ypr(kk),rn_y(kk),rn_x(kk))+1;
end
% compute probabilities and conditional probabilities 计算概率和条件概率
% 这时候的直方图的纵坐标表示频率
Py = Py/(L-delay); % y的概率
Pypr_y = Pypr_y/(L-delay); % y和ypr的概率,这里是联合概率,用矩阵表示
Py_x = Py_x/(L-delay);
Pypr_y_x = Pypr_y_x/(L-delay);
% 没有用高斯核函数等对直方图进行拟合,直接用箱子当做离散点进行计算
Hy = -nansum(Py.*log2(Py)); % 熵
Hypr_y = -nansum(nansum(Pypr_y.*log2(Pypr_y)));
Hy_x = -nansum(nansum(Py_x.*log2(Py_x)));
Hypr_y_x = -nansum(nansum(nansum(Pypr_y_x.*log2(Pypr_y_x))));
% Compute TE
TE(i,j) = Hypr_y + Hy_x - Hy - Hypr_y_x;
end
end
end
TE =
0 0.93
0.094 0
三、相位传递熵
其实相位传递熵跟传递熵的区别是,传递熵直接用信号去统计计算,而相位传递熵先要借助希尔伯特变换将原始信号变为相位,再对信号的相位进行传递熵的计算。道理是一样的,这里直接给出matlab代码。
clc
clear
%% 加载数据
demo_data1 = [3,5,10,5,9,6,4,3,7,4]';
demo_data2 = [2,4,9,4,8,5,3,2,6,3]';
data = [demo_data1,demo_data2];
L = size(data,1); % number of samples 10
N = size(data,2); % number of signal(channel) 2
PTE = zeros(N, N);
%% Compute time series of the phases 计算时间序列的相位
complex_data = hilbert(data); % 希尔伯特变换
phase_data = angle(complex_data);
phase_data = phase_data + pi; % [-π, π]——>[0, 2π],π=3.14
%% 这里使用的论文的'scott'方法计算binsize
binsize = 3.49 * mean(std(phase_data))*L^(-1/3); % binsize as in Scott et al. 箱子宽度
bins_w = [0:binsize:2*pi]; % BINS; NOTE: the last bin has a different size when using 'scott'. Does this matter?
Nbins = length(bins_w);
%% 计算delay,这里我还不明白为什么要这么计算:(
counter1 = 0; counter2 = 0;
for j=1:N
for i=2:L-1
counter1 = counter1 + 1;
if (phase_data(i-1,j)-pi)*(phase_data(i+1,j)-pi)<0, % make sure phase is in range [-pi pi]
counter2 = counter2 + 1;
end;
end;
end;
delay = round(counter1/counter2);
%% 计算PTE
for i = 1:N % 遍历各个导联
for j = 1:N
if i~=j
% y and x are past states. ypr is the observed variable.
Py = zeros(Nbins,1); % y发生的概率
Pypr_y = zeros(Nbins,Nbins); % y and ypr 同时发生的概率
Py_x = zeros(Nbins,Nbins); % y and x 同时发生的概率
Pypr_y_x = zeros(Nbins,Nbins,Nbins); % x、y and ypr同时发生的概率
% ##### 这里是为了方便我自己理解写的
aa_ypr = phase_data(1+delay:end,i); % t时刻的ypr
bb_y = phase_data(1:end-delay,i); % t-delay时刻的y
cc_x = phase_data(1:end-delay,j); % t-delay时刻的x
% #####
rn_ypr = ceil((phase_data(1+delay:end,i)/binsize));
rn_y = ceil((phase_data(1:end-delay,i)/binsize));
rn_x = ceil((phase_data(1:end-delay,j)/binsize));
% 这时候的直方图的纵坐标表示频数
for kk = 1:(L-delay) % L-delay = 10-2=8
Py(rn_y(kk)) = Py(rn_y(kk))+1;% 计数,即统计每个箱子(bin)的样本个数
Pypr_y(rn_ypr(kk),rn_y(kk)) = Pypr_y(rn_ypr(kk),rn_y(kk))+1;
Py_x(rn_y(kk),rn_x(kk)) = Py_x(rn_y(kk),rn_x(kk))+1;
Pypr_y_x(rn_ypr(kk),rn_y(kk),rn_x(kk)) = Pypr_y_x(rn_ypr(kk),rn_y(kk),rn_x(kk))+1;
end
% 计算概率和条件概率
% 这时候的直方图的纵坐标表示频率
Py = Py/(L-delay); % y的概率
Pypr_y = Pypr_y/(L-delay); % y和ypr的概率,这里是联合概率,用矩阵表示
Py_x = Py_x/(L-delay);
Pypr_y_x = Pypr_y_x/(L-delay);
% 没有用高斯核函数等对直方图进行拟合,直接用箱子当做离散点进行计算
Hy = -nansum(Py.*log2(Py)); % 熵
ggggggggg = nansum(Pypr_y.*log2(Pypr_y));
Hypr_y = -nansum(nansum(Pypr_y.*log2(Pypr_y)));
Hy_x = -nansum(nansum(Py_x.*log2(Py_x)));
Hypr_y_x = -nansum(nansum(nansum(Pypr_y_x.*log2(Pypr_y_x))));
% Compute PTE
PTE(i,j) = Hypr_y + Hy_x - Hy - Hypr_y_x;
end
end
end
%% Compute dPTE
tmp = triu(PTE) + tril(PTE)';
dPTE = [triu(PTE./tmp,1) + tril(PTE./tmp',-1)];
dPTE=
0 0.622
0.377 0
python代码,后续继续补充!