机器学习（六）——正则化

我们之前在机器学习（二）——线性回归 和 机器学习（五）——逻辑回归中分别介绍了线性回归算法和逻辑回归算法，并尝试训练我们自己的预测模型。但是有时我们的模型会遇到过拟合的问题，从而导致模型的泛化能力大大降低，使模型的效果很差。本文将通过引入这些问题，介绍正则化技术。

1. 引言

1.1 欠拟合与过拟合

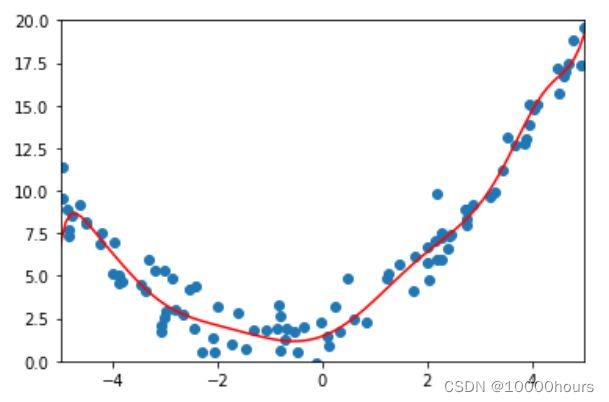
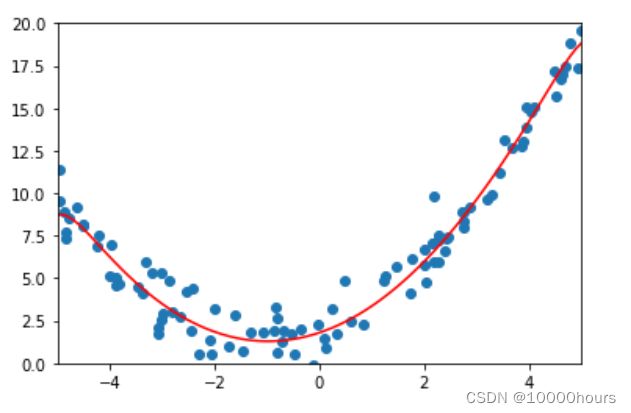
我们先来看这样的回归问题的例子：
注：图片来自吴恩达老师的PPT

假设我们用样本数据拟合出了三个预测模型（如图中所示），我们可以看到：
（1）第一个模型是一条直线，然而这条直线并没有很好地拟合我们的样本数据，这种情况就称为欠拟合；
（2）第二个模型能够较好地拟合我们的样本数据，这个模型似乎是最合适的预测模型；
（3）第三个模型几乎完全拟合了我们的样本数据，但是倘若此时给这个模型一个新值进行预测，这个模型的表现效果就会很差，这种情况就称为过拟合。
同样的，在分类问题中也存在欠拟合与过拟合的情况：

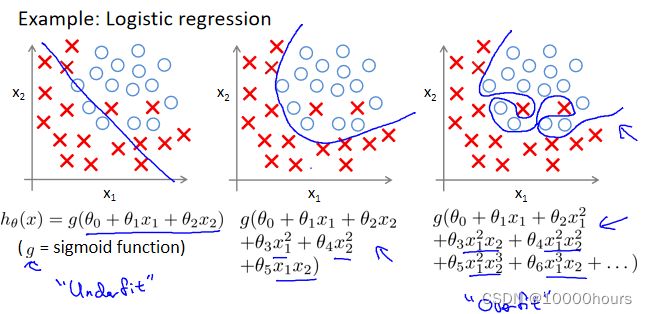
如图所示，第一个模型欠拟合，第三个模型过拟合。

于是我们知道了：
欠拟合：就是模型没有很好的表达样本数据的特征。我们会认为模型存在高偏差问题。
过拟合：就是模型过度强调拟合样本数据，模型在训练集上的表现效果很好，但当输入新的数据进行预测时会表现得很差。我们会认为模型存在高方差问题，即数据的微小扰动都会较大的影响模型。

1.2 解决过拟合问题

在机器学习中主要经常解决的是过拟合的问题。而过拟合主要是由于模型中的高次方项导致的，我们可以理解为次方越高，拟合越好，但是预测能力（泛化能力）可能会变差。

如何解决过拟合问题？既然过拟合问题是由高次方项导致的，那是不是可以通过降低高次方项的影响，来削弱过拟合的影响？考虑如下的解决方法：
（1）丢弃部分特征。我们可以丢弃一些不能帮助我们正确预测的特征，留下对我们预测有利的特征，比如我们可以通过PCA算法来实现。
（2）正则化。正则化不会丢弃特征，它会保留所有的特征，但是会减小参数$\theta$的大小，这样也可以达到降低高次方项的影响。

1.3 引入正则化

我们上面提到了正则化是通过减小参数$\theta$的大小来解决过拟合的问题。来看1.1中回归问题中存在过拟合问题的模型：
$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2^2+{\theta }_3{x}_3^3+{\theta }_4{x}_4^4$$
我们通过减小参数${\theta }_3$和${\theta }_4$的值，从而就可以减小高次方项的影响。

那么其实我们是通过最小化损失函数来得到我们的参数$\theta$的，所以要减小$\theta$要从损失函数入手。我们原始的损失函数是：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
既然我们想要减小${\theta }_3$和${\theta }_4$，那么我们可以添加两项来修改我们的损失函数：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m[(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+10000{\theta }_3^2+10000{\theta }_4^2]$$
我们为${\theta }_3$和${\theta }_4$添加了较大的系数，那么损失函数为了最小化就会相应的减小${\theta }_3$和${\theta }_4$的值，我们的目的就达到了。其中我们添加的项就称为惩罚项。

然而在实际情况中，我们有许多特征，我们不知道需要对哪些特征进行惩罚。因此我们一视同仁，对所有的特征进行惩罚，并让损失函数最优化的软件来选择惩罚的程度。那么我们就得到了一个添加惩罚的损失函数：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2]$$
注：
（1）$\lambda$称为正则化参数；
（2）按照惯例，我们一般不对${\theta }_0$进行惩罚，所以上式中$j$是从1开始的。

如果我们令$\lambda$取较大的值时，为了使损失函数尽可能小，那么相应地参数$\theta$就会在一定程度上减小；但若$\lambda$太大，那么${\theta }_1,{\theta }_2,...,{\theta }_n$都会趋向0，我们最后得到的模型是一条平行x轴的直线，这显然不是我们希望的，所以在进行正则化处理时，要选择一个合适的$\lambda$值。

2. 正则化

2.1 线性回归中的正则化

我们在上文中提到了添加惩罚的线性回归损失函数：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2]$$
接着我们要最小化损失函数，来求参数$\theta$

2.1.1 梯度下降最小化损失函数

我们知道梯度下降算法会一直执行如下操作直至收敛：
$${\theta }_0={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)}$$
$${\theta }_j={\theta }_j-\alpha [\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]forj=1,2,...,n$$
我们通过观察可以发现，正则化之后，每次梯度下降算法更新${\theta }_j$的时候，都在原有基础上多减了一个$\alpha \frac{\lambda }{m}{\theta }_j$项。

2.1.2 正规方程

我们之前在介绍线性回归时也提到了可以通过正规方程来求解$\theta$，$\theta =(X^{T}X{)}^{-1}{X}^{T}y$，那么正则化处理后的$\theta$是：
$$\theta =(X^{T}X+\lambda \left[\begin{array}{ccccc}0& & & & \\ & 1& & & \\ & & 1& & \\ & & & \ddots & \\ & & & & 1\end{array}\right]{)}^{-1}{X}^{T}y$$
式子中的矩阵为$(n+1)\times (n+1)$矩阵，而且对角线上除了第一个元素外都为1，对角线之外的元素都为0.

2.2 逻辑回归中的正则化

我们之前推导的逻辑回归的损失函数为：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$
同样的我们为其添加惩罚项进行正则化处理，得到正则化处理后的损失函数为：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
同样地，使用梯度下降法最小化损失函数，算法一直执行如下操作直到收敛：
$${\theta }_0={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)}$$
$${\theta }_j={\theta }_j-\alpha [\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]forj=1,2,...,n$$

2.3 常用的正则化方法

2.3.1 岭回归 Ridge Regerssion

参考内容：
（1）岭回归百度定义：链接
（2）岭回归介绍文章：链接1 ，链接2，链接3

简单来说，岭回归是一种改进的最小二乘法，它通过损失部分特征信息从而使得回归系数更符合实际、更可靠，对于病态数据（元素的微小变动会引起较大的计算误差，参考百度：病态矩阵）的拟合效果会更好。

岭回归的损失函数为：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2]$$
和上文中的添加了正则项的线性回归损失函数一样，其实岭回归就是在原损失函数中添加L2-范数的正则项，所以岭回归也被称为L2正则化。

2.3.2 LASSO 回归

参考内容：
（1）LASSO百度解释：链接
（2）参考文章：链接1，链接2

LASSO的全称为：Least Absolute Shrinkage and Selection Operator 最小绝对值收敛和选择算子，它通过向原损失函数中添加L1-范数正则项，从而得到更为精确的模型。

LASSO回归的损失函数为：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n|{\theta }_j|]$$

2.3.3 弹性网

参考内容：链接

弹性网络正则化，向原损失函数中添加L1-范数正则项和L2-范数正则项，它的损失函数为：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda p\sum _{j=1}^n|{\theta }_j|+\frac{1-p}{2}\lambda \sum _{ij=1}^n{\theta }_j^2]$$

3.代码实践

我们接着编写代码来尝试实现一下正则化的过程。
注：代码编写和测试均在notebook中进行。

3.1 准备工作

3.1.1 构造多项式回归

使用sklearn中的包来构造我们的多项式回归方法，之后我们使用自己封装好的多项式回归方法来训练预测模型：

from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures, StandardScaler

def PolynomialRegression(degree):
    pipeline = Pipeline([
        ('ploynomial', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('linear_reg', LinearRegression())
    ])
    return pipeline

pipeline是sklearn中的非常好用的一个工具包，它可以将许多算法模型串联起来，更多相关内容可参考：链接

3.1.2 随机生成样本数据

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = np.random.uniform(-5.0, 5.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()

样本数据可视化：

3.2 拟合数据训练模型

输入不同的degree值，观察拟合出来的模型效果。
（1）degree = 2
训练模型：

poly_reg_2 = PolynomialRegression(degree=2)
poly_reg_2.fit(X, y)

预测并计算误差：

y_predict_2 = poly_reg_2.predict(X)
from sklearn.metrics import mean_squared_error
error = mean_squared_error(y, y_predict_2)
print(error)

模型可视化：

（2）degree = 10
训练模型：

poly_reg_10 = PolynomialRegression(degree=10)
poly_reg_10.fit(X, y)

预测并计算误差：

y_predict_10 = poly_reg_10.predict(X)
from sklearn.metrics import mean_squared_error
error_10 = mean_squared_error(y, y_predict_10)
print(error_10)

模型可视化：

（3）degree = 20
训练模型：

poly_reg_20 = PolynomialRegression(degree=20)
poly_reg_20.fit(X, y)

预测并计算误差：

y_predict_20 = poly_reg_20.predict(X)
from sklearn.metrics import mean_squared_error
error_20 = mean_squared_error(y, y_predict_20)
print(error_20)

模型可视化：

（4）degree = 100
训练模型：

poly_reg_100 = PolynomialRegression(degree=100)
poly_reg_100.fit(X, y)

预测并计算误差：

y_predict_100 = poly_reg_100.predict(X)
from sklearn.metrics import mean_squared_error
error_100 = mean_squared_error(y, y_predict_100)
print(error_100)

模型可视化：

说明：
通过上述内容，我们可以看到当degree越大，误差越小，说明我们的模型在努力的拟合样本数据，但是这样的模型就一定越好吗？不一定。我们通过模型的可视化就能看出，当degree越来越大时，模型越曲折，模型过分强调拟合样本数据，但是若输入一个新的数据，模型能否给出较好的预测效果呢？接下来我们就来测试一下。

3.3 过拟合问题

我们先划分样本数据，分为训练集和测试集，用训练集来训练模型，并用测试集来判断我们模型的预测能力。
（1）划分样本数据

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y)

（2）训练模型并测试模型，同样地，通过设置不同的degree得到不同的模型

poly_reg_2 = PolynomialRegression(degree=2)
poly_reg_2.fit(X_train, y_train)
y_predict_2 = poly_reg_2.predict(X_test)
error_2 = mean_squared_error(y_test, y_predict_2)
print("error_2 = ", error_2)

poly_reg_10 = PolynomialRegression(degree=10)
poly_reg_10.fit(X_train, y_train)
y_predict_10 = poly_reg_10.predict(X_test)
error_10 = mean_squared_error(y_test, y_predict_10)
print("error_10 = ", error_10)

poly_reg_20 = PolynomialRegression(degree=20)
poly_reg_20.fit(X_train, y_train)
y_predict_20 = poly_reg_20.predict(X_test)
error_20 = mean_squared_error(y_test, y_predict_20)
print("error_20 = ", error_20)

poly_reg_100 = PolynomialRegression(degree=100)
poly_reg_100.fit(X_train, y_train)
y_predict_100 = poly_reg_100.predict(X_test)
error_100 = mean_squared_error(y_test, y_predict_100)
print("error_100 = ", error_100)

误差：

我们看到degree越大的模型，最终的误差反而越大，这和我们在3.2中得到的结果怎么是反着的呢？我们在3.2中计算的是模型拟合样本数据的误差，degree越大，模型越努力的拟合样本数据，因此误差越小；我们此处计算的是模型在测试集上的误差，degree越大那么模型在训练集上的表现效果越好，但当输入新的数据时，模型的表现效果很差，说明我们的模型出现了过拟合。

3.4 正则化

接下来我们尝试使用正则化的手段来缓解模型的过拟合。
说明：以下测试均采用degree=20， alpha=0.0001。

3.4.1 Ridge Regression

# Ridge Regression

from sklearn.linear_model import Ridge

def RidgeRegression(degree, alpha):
    pipeline = Pipeline([
        ('polynomial', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('ridge_reg', Ridge(alpha=alpha))
    ])
    return pipeline

训练模型：

ridge_reg = RidgeRegression(20, 0.0001)
ridge_reg.fit(X_train, y_train)

预测并计算误差：

y_predict_ridge = ridge_reg.predict(X_test)
error = mean_squared_error(y_test, y_predict_ridge)
print(error)

模型可视化：

3.4.2 LASSO Regression

# LASSO 

from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    pipeline = Pipeline([
        ('polynomial', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('lasso_reg', Lasso(alpha=alpha))
    ])
    return pipeline

训练模型：

lasso_reg = LassoRegression(20, 0.01)
lasso_reg.fit(X_train, y_train)

预测并计算误差：

y_predict_lasso = lasso_reg.predict(X_test)
error = mean_squared_error(y_test, y_predict_lasso)
print(error)

模型可视化：

3.4.3 弹性网

# 弹性网

from sklearn.linear_model import ElasticNet

def ElasticNet_(degree, alpha):
    pipeline = Pipeline([
        ('polynomial', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('elas_net', ElasticNet(alpha=alpha))
    ])
    return pipeline

训练模型：

elas_net = ElasticNet_(20, 0.01)
elas_net.fit(X_train, y_train)

预测并计算误差：

y_predict_elas = elas_net.predict(X_test)
error = mean_squared_error(y_test, y_predict_elas)
print(error)

模型可视化：

3.4.4 比较

我们将正则化后得到的模型的预测误差，与先前的误差进行比较（此处比较的是degree=20的模型），我们可以看到误差有所减小，说明正则化处理后我们的模型的泛化能力有所提高。

4. 总结

（1）我们首先引入了模型的过拟合问题，并说明了过拟合会带来的问题，由此提出了使用正则化的手段来解决模型的过拟合；
（2）之后我们介绍了如何在线性回归和逻辑回归中使用正则化：通过为损失函数添加惩罚项来减小$\theta$；
（3）接着我们介绍了几种常用的正则化方式：岭回归、LASSO回归、弹性网；
（4）最后我们通过编写代码，使用多项式回归，处理模型过拟合，并尝试实践了三种正则化方式。

至此，本篇就接近尾声了，需要说明一下：
由于本人也是初学者，文章内容可能会有错误和不足，非常欢迎大家指正和补充！