文本表示（Representation）

文本表示（Representation）

自然语言处理问题中，一般以词作为基本单元，例如我们想要分析“我爱中国”这句话的情感，一般的做法是先将这句话进行分词，变成我,爱,中国。由于神经网络无法处理词，所以我们需要将这些词通过某些办法映射成词向量。词向量可以被认定为词的特征向量，可以用作代表这个词。通常把词映射为实数领域向量的技术也叫词嵌入(Word embedding).

独热编码(one-hot representation)

假如我们要计算的文本中一共出现了4个词：猫、狗、牛、羊。向量里每一个位置都代表一个词。所以用one-hot来表示就是：

• 猫： $$[1,0,0,0]$$
• 猫: $$[1,0,0,0]$$
• 狗: $$[0,1,0,0]$$
• 牛: $$[0,0,1,0]$$
• 羊: $$[0,0,0,1]$$

但是在实际情况中，文本中很可能出现成千上万个不同的词，这时候向量就会非常长。其中大部分都是0填充。

one-hot的缺点如下：

1. 无法表达词语之间的关系
2. 这种过于稀疏的向量，导致计算和存储的效率都不高

整数编码

这种方式也非常好理解，用一种数字来代表一个词，对应钱买你的例子则是：

• 猫 : 1
• 狗：2
• 牛：3
• 羊：4

将句子里的每个词拼起来就是可以表示一句话的向量。

整数编码的缺点如下：

1. 无法表达词语之间的关系
2. 对于模型解释而言，整数编码可能具有挑战性

Word2vec

Word2vec 是google在2013年推出的一个NLP工具，它的特点是能够将单词转化为向量来表示，这样词与词之间就可以定量的去度量它们之间的关系。挖掘词之间的联系。

模型整体理解

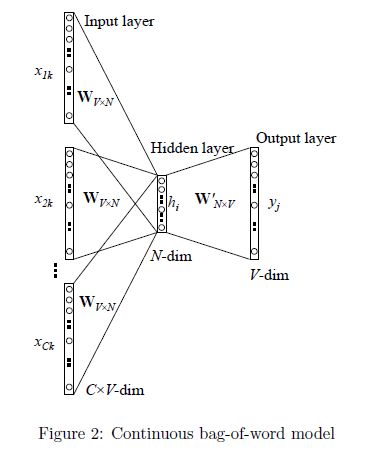
Word2vec的训练模型本质上是只具有一个隐含层的神经元网络，如下图：

它的输入是采用One-Hot编码的词汇表向量，它的输出也是One-Hot编码的词汇表向量。使用所有的样本，训练这个神经元网络，等到收敛之后，从输入层到隐含层的那些权重，便是每一个词的Distributed Representation的词向量。比如，上图单词的Word embedding后的向量便是矩阵$W_{V\ast N}$的第i行的转置。这样我们就把原本维度为$V$的词向量变成了维数为N的词向量，并且词向量间保留了一定的相关关系。

Google在关于Word2Vec的论文中提出了CBOW和Skip-gram两种模型，CBOW适合于数据集较小的情况，而Skip-Gram在大型语料中表现更好。其中CBOW如上图左部分所示，使用围绕目标单词的其他单词作为输入，在映射层做加权处理后输出目标单词。与CBOW根据语境预测目标单词不同，Skip-gram根据当前单词预测语境，如下图右部分所示。假如我们有一个句子“There is an apple on the table”作为训练数据，CBOW的输入为（is,an,on,the）,输出为apple.而Skip-gram的输入为apple，输出为（is, an, on , the）。

我的理解

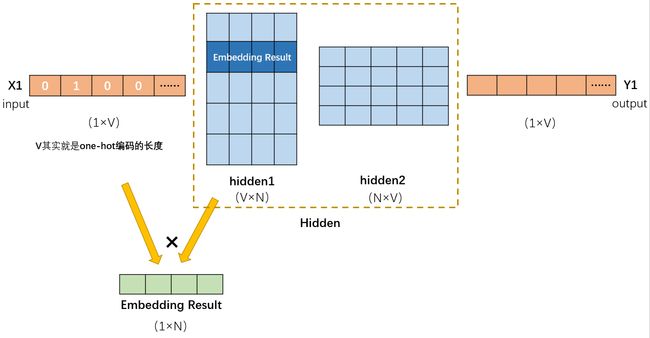
好吧，上面这些是从其它地方copy来的。其实讲得挺好的了，大致可以理解其中的工作原理。我又针对其中的细节进行进一步分析，可以根据下图进一步梳理其中的运作流程（将上述将上面的输入输出流程拆分为最小单元，即输入一个字的one-hot得到一个输出结果，例如输入一个$x_1$得到一个$Y_1$）：

单纯看这幅图可能还有的疑问

• 输入的是什么？输入的向量如何来的？
• 输出的结果是什么？输出的结果想要是什么？
• 中间Hidden层里面有两层作用分别是什么？
• 如果已经对模型进行过了训练，那么$$x_1$$的Embedding结果是什么，怎么获得？

✔解答

这个解答可以对照着前面的文字去看

1. 输入的其实就是 one-hot编码

2. 输出的结果想要的就是另外一个one-hot编码，那么另外一个one-hot是谁呢？这个其实就是CBOW和Skip-gram这两个模型所要做的事情。比如在训练时遇到了句子中第$t$个字$w_t$ CBOW是依次(当然可以一起)将$w_t$周围的几个字进行输入希望得到$w_t$这个字的one-hot。而 Skip-gram设计的是将$w_t$这个字作为输入希望依次得到周围几个字的one-hot编码。

3. 其实word2vec这个模型其实就是类似于一个encode和decode的架构。不过我们在编码和解码的过程中想要得到的输入输出的one-hot是不一样的，里面其实就是有一些网络随机的成分在里面。（也正是输入输出是不一样的所以，通过梯度下降的方式可以让一个单词的编码包含不同维度的信息，而不是one-hot那样子只有一个维度的信息而且与其他词之间的one-hot的距离都一样）。所以对应的上面的hidden1可以简单理解为encode层,hidden2为decode层。

4. 经过第三小问，我们将这个Hidden理解为encode和decode的架构。要得$x_1$的 Embedding结果就是也就是encode的结果嘛，对应的就是将$x_1$的one-hot向量与hidden1进行矩阵乘法的结果。

   上面所说的其实我们确实可以得到 Embedding的结果，不过我们还可以更具one-hot向量的特点进行简化。我们知道one-hot编码中只有一个维度是1其它维度都是用0表示，所以矩阵乘法的结果就是hidden1中对应的第$i$行。（我在hidden1中用更深的蓝色突出显示了）

CBoW & Skip-gram Model

下面所举例的句子都为：“There is an apple on the table”。

CBOW

1. 输入层：上下文单词的one-hot编码向量，V为词汇单词个数，C为上下文单词个数。所以以前面的句子为例，对于apple这个词。这里C=4,所以模型的输入是(is，an,on,the)4个单词的one-hot编码词向量。
2. 初始化一个权重矩阵$W_{V\times N}$(对应前面的hidden1),然后用所有输入的 one-hot 编码词向量左乘该矩阵，得到维数为N的向量 $w_1,w_2,...,w_c$，这里N就是想要得到的Word2vec编码的向量维数。
3. 将所得向量$w_1,w_2,...,w_c$相加求平均作为隐藏层向量h.
4. 初始化另一个权重矩阵$W_{N\times V}^{{}^{\prime }}$，用隐藏层向量h左乘$W_{N\times V}^{{}^{\prime }}$，再经过激活函数处理得到V维的向量y,y的每个元素代表相对应的每个单词的概率分布(也可以直接理解为one-hot)。
5. y中概率最大的元素所指示的单词为预测出的中间词（target word）与true label 的one-hot编码向量做比较，误差越小越好（根据误差更新两个权重矩阵）。

Skip-gram

同样的对于apple这个词在上述句子环境中。与CBOW不同的是Skip-gram选apple的one-hot作为输入。如果我们设置skip_window=2的话，那么target word其实就是[“is”, “an”, “on”, “the”].其他的部分都和 CBOW 一样。

改进方案

在前面的小结中，我们介绍了CBOW和Skip-gram在理想情况下的实现，即训练迭代两个举证$W$和$W^{{}^{\prime }}$，之后在输出层采用softmax函数来计算输出各个词的概率。但是在实际应用中这种方法的训练开销很大，所以提出了Hierarchical Softmax和Negative Sampling两种该进方法。

Hierarchical Softmax

Hierarchical Softmax对原模型的该进主要有两点：

1. （主要针对CBOW方案）从输入层到隐藏层的映射时，没有采用周围词与hidden1相乘后相加求平均的方法，而是直接对所有输入的词向量求和。
2. 采用哈夫曼树来替换原先的从隐藏层到输出层的矩阵$W^{{}^{\prime }}$，一个叶子节点代表一个单词，而从根节点到该叶子节点的路径确定了这个单词最终输出的词向量。

Negative Sampling

负采样（Negative Sampling）是另外一种用来提高Word2Vec效率的方法，它是基于这样的观察：训练一个神经网络意味着使用一个训练样本就要稍微调整一下神经网络中所有的权重，如果能够设计一种一次值更新一部分权重的方法，那么计算复杂度将大大降低。

负采样其实做的就是选取一部分单词进行训练，比如在文本中“the”这样的常用词出现概率很大，因此我们在训练的过程中会将大量的“the”加入到训练的过程中，而这些样本数量圆圆超过了我们学习“the”这个词所需要的训练样本数。因此需要通过“抽样”模式来解决这种高频词问题。它的基本思想如下：对于我们在训练原始文本中的每一个单词，它们都有一定概率被我们从文本中删掉，而这个被删除的概率于单词的频率有关。当一个词的出现频次越高这个单词越容易被选作为negtive words。

代码

下面是未优化前的代码实现

""""尝试自己完成代码"""
import sys
import jieba
import numpy as np
import pandas as pd
import os
import pickle
from tqdm import tqdm

def cut_words(filepath="./日志数据.txt"):
    stop_words = r'.。、!?？！……'
    result = []
    jieba.load_userdict("./my_dict_new.txt") 
    all_data = open(filepath,"r",encoding="utf-8")
    all_data = list(all_data)
    for sentence in all_data[:]:
        sentence = sentence[:-1]
        # cut_words  = jieba.lcut(sentence)
        cut_words  = jieba.cut(sentence, HMM=True,cut_all=False)
        result.append([word for word in cut_words if word not in stop_words])   #添加切好词并去除部分停用词
    return result

def get_dict(data):
    # 获取三个准备的数据
    index_2_word = []   #index -> word   且词语不会重复
    for words in data:
        for word in words:
            if word not in index_2_word:
                index_2_word.append(word)
            
    word_2_index = {word:index for index,word in enumerate(index_2_word)}         #word -> index
    words_size = len(word_2_index)
    word_2_onehot = {}
    for word,index in word_2_index.items():
        one_hot = np.zeros((1,words_size))       #构造1 * 
        one_hot[0,index] = 1
        word_2_onehot[word] = one_hot
    
    return word_2_index,index_2_word,word_2_onehot

def softmax(x):
    """
        # 激活函数
    """
    ex = np.exp(x)
    return ex/np.sum(ex,axis = 1,keepdims = True)

def train(embedding_num = 107,lr = 0.01,epoch = 10,n_gram = 3):
    data = cut_words()
    word_2_index,index_2_word,word_2_onehot = get_dict(data)

    word_size = len(word_2_index)
    """
        # embedding_num = 107    #设置维度
        # lr = 0.01
        # epoch = 10     #训练的次数
        # n_gram = 3     #设置相关词数
    """

    w1 = np.random.normal(-1,1,size = (word_size,embedding_num))
    w2 = np.random.normal(-1,1,size = (embedding_num,word_size))

    for e in range(epoch):
        for words in tqdm(data):
            for n_index,now_word in enumerate(words):
                now_word_onehot = word_2_onehot[now_word]
                other_words = words[max(n_index - n_gram,0):n_index] + words[n_index+1 : n_index+1+n_gram]  #获取前后一定范围的关联词
                # 使用上下文中的每一个字进行拟合
                for other_word in other_words:
                    other_word_onehot = word_2_onehot[other_word]
                    hidden = now_word_onehot @ w1
                    p = hidden @ w2
                    # pre 是通过隐藏层并通过激活函数后得到的值
                    pre = softmax(p)
                    """矩阵求导公式
                        # loss = -np.sum(other_word_onehot * np.log(pre)) 
                        # A @ B = C   
                        # delta_C = G
                        # delta_A = G @ B.T
                       0 # delta_B = A.T @ G
                    """

                    # 计算出这个激活函数出来的结果跟周围单词的差距
                    # G2 ->  1 * wordSize
                    # 输出的字向量和onehot的差
                    G2 = pre - other_word_onehot
                    delta_w2 = hidden.T @ G2
                    # G1 -> 1 * embedding
                    G1 = G2 @ w2.T
                    # 获得于这个字的向量然后去拟合
                    delta_w1 = now_word_onehot.T @ G1
                    print(delta_w1)
                    sys.exit(0)

                    w1 -= lr * delta_w1
                    w2 -= lr * delta_w2
    
    with open("word2vec.pkl","wb") as f:   #保存训练结果
        pickle.dump([w1,word_2_index,index_2_word],f)    #负采样

def predict(word,top_n):
    try:
        w1,word_2_index,index_2_word = pickle.load(open("my_word2vec.pkl","rb"))
        v_w1 = w1[word_2_index[word]]
        word_sim = {}
        for  i in range(len(word_2_index)):
            v_w2 = w1[i]
            theta_sum = np.dot(v_w1 , v_w2)
            theta_den = np.linalg.norm(v_w1) * np.linalg.norm(v_w2)
            theta = theta_sum / theta_den
            word = index_2_word[i]
            word_sim[word] = theta
        words_sorted = sorted(word_sim.items(), key=lambda kv : kv[1],reverse=True)
        for word,sim in words_sorted[:top_n]:
            print(word,sim)
    except KeyError:
        print(word+" Not found words")

if __name__ == '__main__':
    train()

使用 gensim包的实现

"""gensim包中Word2vec模块的使用"""

import jieba
from gensim.models import Word2Vec
from gensim.models.word2vec import LineSentence

#获得需要训练的数据
def get_train_data(filePath = r"./日志数据.txt"):
    jieba.load_userdict("./my_dict_new.txt")
    passage = open(filePath,"r",encoding="utf-8")
    stop_words = r".。、，,/\!?……"
    data = []
    for line in list(passage)[:]:
        line = line[:-1]
        cut_words  = jieba.cut(line, HMM=True,cut_all=False)
        data.append([word for word in cut_words if word not in stop_words])
    passage.close()
    return data

#模型训练
def train_model(savepath="./gensim.model"):
    sentences = get_train_data()    #获得分好词的数据
    model = Word2Vec(sentences, sg=1 , window=5,  min_count=5,  negative=3, sample=0.001, hs=1, workers=4)
    model.save(savepath) 
    model.wv.save_word2vec_format("./model_details.txt", binary=False)

# 使用训练得到的模型进行相关词预测
def predict(model_path = "./gensim.model"):
    my_predict_words = ["机组","小机","磨煤机","风机","ren"]
    model = Word2Vec.load(model_path)
    for word in my_predict_words:
        try:
            similar_word = model.wv.most_similar(word,topn=10)
            print(word,similar_word)
        except KeyError:
            print(word+"  not in data")

if __name__ == "__main__":
    train_model()
    predict()

Glove

Glove的全称叫做Global Vectors for Word Representation,它是基于全局词频统计的词表征工具，它可以把一个单词表达成一个由实数组成的向量，这些向量捕捉到了单词之间的一些语义特性，比如相似性、类比性等。我们通过对向量的运算，可以计算得到单词之间的语义相似性。

Glove的实现

Glove的实现分为以下三步：

1. 根据语料构建一个共现矩阵X，矩阵中的每一个元素 $X_{ij}$代表单词$i$和上下文单词$j$在特定大小的上下文窗口内共同出现的次数。一般而言，这个次数的最小单位是1，但是Glove根据两个单词在上下问窗口的距离d，提出了一个衰减函数：$decay=1/d$ 用于计算权重，也就是说距离越远的两个单词所占总计数的权重越小。

2. 构建词向量和共现矩阵之间的近似关系，论文的作者提出以下的公式可以近似地表达两者之间的关系：$w_i^T{w}_j^{-}+b_i+b_j^{-}=log(X_{ij})$.其中$w_i^T和w_j^{-}$其中$w_i^T$和$w_{-}j$是我们最终要求解的词向量；$b_i$和$b_j^{-}$分别是两个词向量的bias term

3. 有了卡面的公式之后我们可以构造它的loss function:
   $$J=\sum _{i，j}^{V}f(X_{ij})(w_i^T{w}_j^{-}+b_i+b_j-log(X_{ij}){)}^2$$
   这个loss function 的基本形式就是最简单的mean square loss，只不过在此基础上加了一个权重函数$f(X_{ij})$，那么这个函数起了什么作用，为什么要添加这个函数呢？这个其实就跟word2vec中要进行负采样的原因是差不多的，我们希望：

   • 这些单词的权重要大于那些很少在一起出现的单词，所以这个函数要是非递减的函数。

   • 但我们也不希望这个权重过大，当到达一定程度之后应该不再增加

   • 如果两个单词没有在一起出现，也就是$X_{ij}=0$，那么他们应该不参到loss function的计算中去，也就是$f(x)$要满足$f(0)=0$

     满足以上两个条件的函数有很多，作者采用了如下形式的分段函数：
     $$f(x)=\{\begin{array}{ll}(x/x_{max}{)}^a& ifx<x_{max}\\ 1& otherwise\end{array}$$

     

模型代码

class GloVe(nn.Module):
 
    def __init__(self, vocab_size, embedding_size, x_max, alpha):
        super().__init__()
        self.weight = nn.Embedding(
            num_embeddings=vocab_size,
            embedding_dim=embedding_size,
            sparse=True
        )
        self.weight_tilde = nn.Embedding(
            num_embeddings=vocab_size,
            embedding_dim=embedding_size,
            sparse=True
        )
        self.bias = nn.Parameter(
            torch.randn(
                vocab_size,
                dtype=torch.float,
            )
        )
        self.bias_tilde = nn.Parameter(
            torch.randn(
                vocab_size,
                dtype=torch.float,
            )
        )
        self.weighting_func = lambda x: (x / x_max).float_power(alpha).clamp(0, 1)
 
    def forward(self, i, j, x):
        loss = torch.mul(self.weight(i), self.weight_tilde(j)).sum(dim=1)
        loss = (loss + self.bias[i] + self.bias_tilde[j] - x.log()).square()
        loss = torch.mul(self.weighting_func(x), loss).mean()
        return loss

模型的输入就是共现矩阵的那个matrix，而这个遍历的过程其实就是去遍历遍历其中的每一个单元

参考

• glove
• word2vec负采样理解
• word2vec详解