数据挖掘实践(金融风控-贷款违约预测)(一):赛题理解
数据挖掘实践(金融风控-贷款违约预测)(一):赛题理解
目录
- 数据挖掘实践(金融风控-贷款违约预测)(一):赛题理解
-
- 1 引言
- 2 赛题介绍
-
- 2.1 数据概况
- 2.2 预测指标
-
- 2.2.1 分类算法常见的评估指标
- 2.2.2 金融风控预测类常见的评估指标
- 3 实战
- 4 总结
- 【参考资料】
1 引言
本次新人赛是Datawhale与天池联合发起的0基础入门系列赛事第四场——零基础入门金融风控之贷款违约预测挑战赛。赛题以金融风控中的个人信贷为背景,要求选手根据贷款申请人的数据信息预测其是否有违约的可能,以此判断是否通过此项贷款,这是一个典型的分类问题。通过这道赛题来引导大家了解金融风控中的一些业务背景,解决实际问题,帮助竞赛新人进行自我练习、自我提高。
项目地址:https://github.com/datawhalechina/team-learning-data-mining/tree/master/FinancialRiskControl
比赛地址:https://tianchi.aliyun.com/competition/entrance/531830/introduction
2 赛题介绍
比赛要求参赛选手根据给定的数据集,建立模型,预测金融风险。
赛题以预测金融风险为任务,数据集报名后可见并可下载,该数据来自某信贷平台的贷款记录,总数据量超过120w,包含47列变量信息,其中15列为匿名变量。为了保证比赛的公平性,将会从中抽取80万条作为训练集,20万条作为测试集A,20万条作为测试集B,同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。
2.1 数据概况
一般而言,对于数据在比赛界面都有对应的数据概况介绍(匿名特征除外),说明列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。
注:匿名特征,就是未告知数据列所属的性质的特征列。
train.csv
- id 为贷款清单分配的唯一信用证标识
- loanAmnt 贷款金额
- term 贷款期限(year)
- interestRate 贷款利率
- installment 分期付款金额
- grade 贷款等级
- subGrade 贷款等级之子级
- employmentTitle 就业职称
- employmentLength 就业年限(年)
- homeOwnership 借款人在登记时提供的房屋所有权状况
- annualIncome 年收入
- verificationStatus 验证状态
- issueDate 贷款发放的月份
- purpose 借款人在贷款申请时的贷款用途类别
- postCode 借款人在贷款申请中提供的邮政编码的前3位数字
- regionCode 地区编码
- dti 债务收入比
- delinquency_2years 借款人过去2年信用档案中逾期30天以上的违约事件数
- ficoRangeLow 借款人在贷款发放时的fico所属的下限范围
- ficoRangeHigh 借款人在贷款发放时的fico所属的上限范围
- openAcc 借款人信用档案中未结信用额度的数量
- pubRec 贬损公共记录的数量
- pubRecBankruptcies 公开记录清除的数量
- revolBal 信贷周转余额合计
- revolUtil 循环额度利用率,或借款人使用的相对于所有可用循环信贷的信贷金额
- totalAcc 借款人信用档案中当前的信用额度总数
- initialListStatus 贷款的初始列表状态
- applicationType 表明贷款是个人申请还是与两个共同借款人的联合申请
- earliesCreditLine 借款人最早报告的信用额度开立的月份
- title 借款人提供的贷款名称
- policyCode 公开可用的策略_代码=1新产品不公开可用的策略_代码=2
- n系列匿名特征 匿名特征n0-n14,为一些贷款人行为计数特征的处理
2.2 预测指标
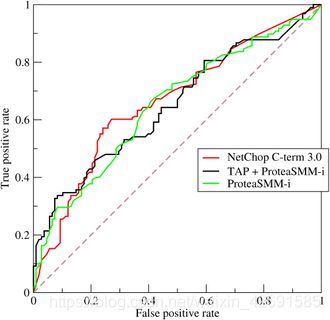
竞赛采用AUC作为评价指标。AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积。
2.2.1 分类算法常见的评估指标
1、混淆矩阵(Confuse Matrix)
混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。其中矩阵的行表示真实值,矩阵的列表示预测值,以分类模型中最简单的二分类为例,对于这种问题,我们的模型最终需要判断样本的结果是0还是1,或者说是positive还是negative。
我们通过样本的采集,能够直接知道真实情况下,哪些数据结果是positive,哪些结果是negative。同时,我们通过用样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。
因此,我们就能得到这样四个基础指标,我称他们是一级指标(最底层的):
- 真实值是positive,模型认为是positive的数量(True Positive=TP)
- 真实值是positive,模型认为是negative的数量(False Negative=FN):这就是统计学上的第二类错误(Type II Error)
- 真实值是negative,模型认为是positive的数量(False Positive=FP):这就是统计学上的第一类错误(Type I Error)
- 真实值是negative,模型认为是negative的数量(True Negative=TN)
将这四个指标一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵(Confusion Matrix):
(1)若一个实例是正类,并且被预测为正类,即为真正类TP(True Positive )
(2)若一个实例是正类,但是被预测为负类,即为假负类FN(False Negative )
(3)若一个实例是负类,但是被预测为正类,即为假正类FP(False Positive )
(4)若一个实例是负类,并且被预测为负类,即为真负类TN(True Negative )
2、准确率(Accuracy)
准确率是常用的一个评价指标,但是不适合样本不均衡的情况。
Accuracy = \frac{TP + TN}{TP + TN + FP + FN}
3、精确率(Precision)
又称查准率,正确预测为正样本(TP)占预测为正样本(TP+FP)的百分比。
Precision = \frac{TP}{TP + FP}
4、召回率(Recall)
又称为查全率,正确预测为正样本(TP)占正样本(TP+FN)的百分比。
Recall = \frac{TP}{TP + FN}
5、F1 Score
精确率和召回率是相互影响的,精确率升高则召回率下降,召回率升高则精确率下降,如果需要兼顾二者,就需要精确率、召回率的结合F1 Score。
F1-Score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}
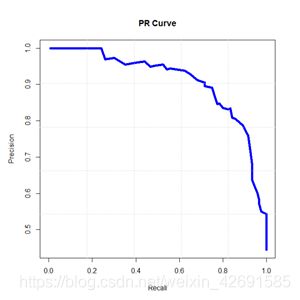
6、P-R曲线(Precision-Recall Curve)
P-R曲线是描述精确率和召回率变化的曲线,如下:
7、ROC(Receiver Operating Characteristic)
ROC空间将假正例率(FPR)定义为 X 轴,真正例率(TPR)定义为 Y 轴。
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
TPR = \frac{TP}{TP + FN}
FPR:在所有实际为负例的样本中,被错误地判断为正例之比率。
FPR = \frac{FP}{FP + TN}

8、AUC(Area Under Curve)
AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
2.2.2 金融风控预测类常见的评估指标
1、KS(Kolmogorov-Smirnov)
KS统计量由两位苏联数学家A.N. Kolmogorov和N.V. Smirnov提出。在风控中,KS常用于评估模型区分度。区分度越大,说明模型的风险排序能力(ranking ability)越强。 K-S曲线与ROC曲线类似,不同在于
- ROC曲线将真正例率和假正例率作为横纵轴
- K-S曲线将真正例率和假正例率都作为纵轴,横轴则由选定的阈值来充当。
公式如下: KS=max(TPR-FPR)
KS不同代表的不同情况,一般情况KS值越大,模型的区分能力越强,但是也不是越大模型效果就越好,如果KS过大,模型可能存在异常,所以当KS值过高可能需要检查模型是否过拟合。以下为KS值对应的模型情况,但此对应不是唯一的,只代表大致趋势。
| KS(%) | 好坏区分能力 |
|---|---|
| 20以下 | 不建议采用 |
| 20-40 | 较好 |
| 41-50 | 良好 |
| 51-60 | 很强 |
| 61-75 | 非常强 |
| 75以上 | 过于高,疑似存在问题 |
2、ROC(Receiver Operating Characteristic)
ROC空间将假正例率(FPR)定义为 X 轴,真正例率(TPR)定义为 Y 轴。
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
TPR = \frac{TP}{TP + FN}
FPR:在所有实际为负例的样本中,被错误地判断为正例之比率。
FPR = \frac{FP}{FP + TN}
3、AUC(Area Under Curve)
AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
3 实战
# 数据读取pandas
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
train = pd.read_csv('train.csv')
testA = pd.read_csv('testA.csv')
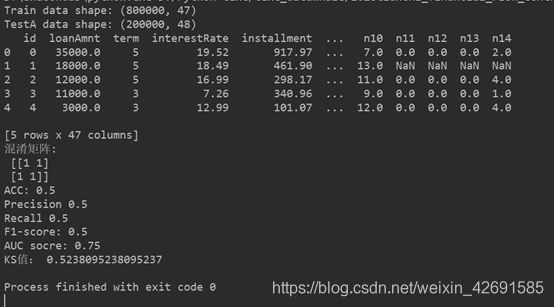
print('Train data shape:', train.shape)
print('TestA data shape:', testA.shape)
# Train data shape: (800000, 47)
# TestA data shape: (200000, 48)
print(train.head())
# 分类指标评价计算示例
# 混淆矩阵
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('混淆矩阵:\n', confusion_matrix(y_true, y_pred))
# accuracy
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('ACC:', accuracy_score(y_true, y_pred))
# Precision,Recall,F1-score
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('Precision', metrics.precision_score(y_true, y_pred))
print('Recall', metrics.recall_score(y_true, y_pred))
print('F1-score:', metrics.f1_score(y_true, y_pred))
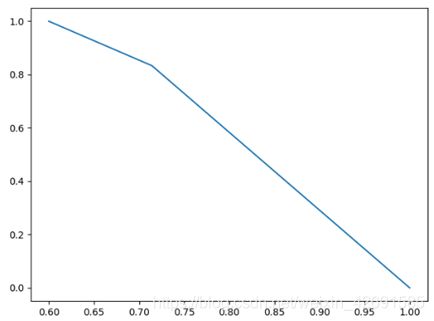
# P-R曲线
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision, recall, thresholds = precision_recall_curve(y_true, y_pred)
plt.plot(precision, recall)
plt.show()
# ROC曲线
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR, TPR, thresholds = roc_curve(y_true, y_pred)
plt.title('ROC')
plt.plot(FPR, TPR, 'b')
plt.plot([0, 1], [0, 1], 'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')
plt.show()
# AUC
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:', roc_auc_score(y_true, y_scores))
# KS值 在实际操作时往往使用ROC曲线配合求出KS值
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
FPR, TPR, thresholds = roc_curve(y_true, y_pred)
KS=abs(FPR-TPR).max()
print('KS值:', KS)
结果:
4 总结
赛题理解是开始比赛的第一步,赛题的理解有助于对竞赛全局的把握。通过赛题理解有助于对赛题的业务逻辑把握,对于后期的特征工程构建和模型选择都尤为重要。
- 在开始比赛之前要对赛题进行充分的了解。
- 比赛什么时候开始,什么时候结束,什么时候换B榜数据。
- 和该比赛有没有类似的比赛可以参考借鉴。
- 线上提交结果的次数往往是有限的,提前了解每日可以提交的次数。
- 比赛使用的是什么评价指标,可以选择相同的评价指标作为线下验证的方式。
【参考资料】
- 数据挖掘实践(金融风控)
- 零基础入门数据挖掘 - 贷款违约预测