pytorch学习线性回归与非线性回归,以及理解nn.linear()和ReLU激活函数
参考书目:Pytorch深度学习入门,作者:曾芃壹
文章目录
- 线性回归
-
- 线性模型与目标函数
- 优化
- 批量输入
- 代码实践
- 大规模数据实验
- 神经网络实现线性回归
- 非线性回归
-
- 激活函数
- 人工神经网络
- 详解nn.linear()的原理
- 浅谈ReLU激活函数在本例中的作用
线性回归
线性模型与目标函数
这次我们使用直线KaTeX parse error: \tag works only in display equations来拟合几个离散点,个点的 值如下
| x ( i ) x^{(i)} x(i) | y ( i ) y^{(i)} y(i) | y ^ ( i ) \widehat{y}^{(i)} y (i) |
|---|---|---|
| 1.4 1.4 1.4 | 14.4 14.4 14.4 | 14.4 w 1 + w 0 14.4w_1+w_0 14.4w1+w0 |
| 5 5 5 | 29.6 29.6 29.6 | 5 w 1 + w 0 5w_1+w_0 5w1+w0 |
| 11 11 11 | 62 62 62 | 11 w 1 + w 0 11w_1+w_0 11w1+w0 |
| 16 16 16 | 85.5 85.5 85.5 | 16 w 1 + w 0 16w_1+w_0 16w1+w0 |
| 21 21 21 | 113.4 113.4 113.4 | 21 w 1 + w ) 21w_1+w_) 21w1+w) |
优化
损失函数(均方误差):
L ( w 1 , w 0 ) = ∑ i = 1 5 ( w 1 x ( i ) + w 0 − y ( i ) ) 2 (1-2) L(w_1,w_0)=\sum\limits_{i=1}^5(w_1x^{(i)}+w_0-y^{(i)})^2\tag{1-2} L(w1,w0)=i=1∑5(w1x(i)+w0−y(i))2(1-2)
L L L的梯度
∇ L = ( ∂ L ∂ w 1 , ∂ L ∂ w 0 ) (1-3) \nabla L=\big(\cfrac{\partial L}{\partial w_1},\cfrac{\partial L}{\partial w_0}\big)\tag{1-3} ∇L=(∂w1∂L,∂w0∂L)(1-3)
将 ( w 0 , w 1 ) (w_0,w_1) (w0,w1)看做向量则梯度下降可以写为:
w → t + 1 = w → t − ∇ L ( w → t ) × δ (1-4) \overrightarrow{w}^{t+1}=\overrightarrow{w}^t-\nabla L (\overrightarrow{w}^t)\times\delta\tag{1-4} wt+1=wt−∇L(wt)×δ(1-4)
∇ L ( w → t ) \nabla L (\overrightarrow{w}^t) ∇L(wt)可以由自动微分autograd技术得到。
批量输入
把式(1-1)写成向量形式,把 w 0 w_0 w0看做 w 0 × x 0 w_0\times x_0 w0×x0其中 x 0 = 1 x_0=1 x0=1,则
y ^ = x → ⋅ w → (1-5) \widehat{y}=\overrightarrow{x} \cdot \overrightarrow{w}\tag{1-5} y =x⋅w(1-5)
损失函数 L L L也可写为:
L ( w 1 , w 0 ) = ∣ y ^ → − y → ∣ 2 L(w_1,w_0)=\left |\overrightarrow{\widehat{y}}-\overrightarrow{y} \right|^2 L(w1,w0)=∣∣∣y −y∣∣∣2
代码实践
import torch
import matplotlib.pyplot as plt
#产生输入X,X有两个维度n行2列,2列对应x1w1+x0w0,x0=1
def Produce_X(x):
x0=torch.ones(x.numpy().size)#x.numpy()将Tensor转化为numpy
X=torch.stack((x,x0),dim=1)#将x与x0在第二个维度进行连接组合成n行2列的矩阵
return X
x=torch.Tensor([1.4,5,11,16,21])
Y=torch.Tensor([14.4,29.6,62,85.5,113.4])
X=Produce_X(x)
#输入与目标函数结果
inputs=X
target=Y
w=torch.rand(2,requires_grad=True)#设置参数w开启自动微分
#X的实际结构
X
tensor([[ 1.4000, 1.0000],
[ 5.0000, 1.0000],
[11.0000, 1.0000],
[16.0000, 1.0000],
[21.0000, 1.0000]])
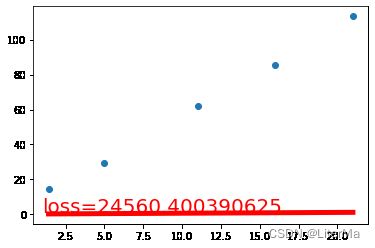
#训练前
draw(inputs.mv(w),loss = (inputs.mv(w) - target).pow(2).sum())
# 训练
def train(epochs=1, learning_rate=0.01):
for epoch in range(epochs):
output = inputs.mv(w)
loss = (output - target).pow(2).sum()
loss.backward()
w.data -= learning_rate * w.grad
w.grad.zero_() # 调用zero_函数清空grad属性值,避免grad值持续积累
#由于篇幅问题我们只画出最开始的直线和最后训练出的直线
#if epoch % 80 == 0: # 每80个epoch
# draw(output, loss)
return w, loss
def draw(output, loss): #
plt.cla() # 清除当前活动轴
plt.scatter(x.numpy(), Y.numpy())
plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5) # 红色,宽度5
plt.text(1, 2, 'loss=%s' % (loss.item()), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.005)
w, loss = train(10000, learning_rate=1e-4)
print("final loss:", loss.item()) # item将Tensor的单一张量转化为python的元素值
# 如果我们想要修改 tenso r的数值,但是又不希望被autograd记录,那么我么可以对 tensor.data 进行操作
print("weight:", w.data)
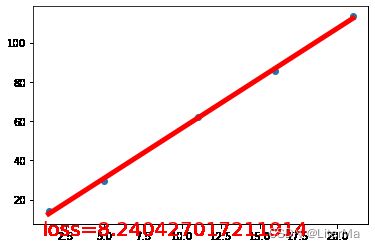
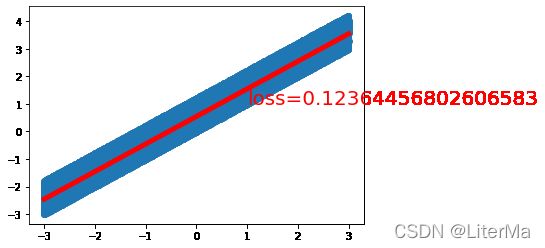
#训练后再画直线
draw(inputs.mv(w),loss = (inputs.mv(w) - target).pow(2).sum())
final loss: 8.24051284790039
weight: tensor([5.0838, 5.5881])
大规模数据实验
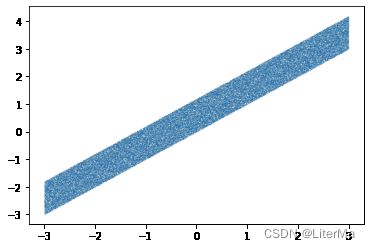
使用linspace函数在(-3,3)之间划分100000个点,并在y轴上增加一些误差
代码在训练部分不变,在数据初始化和draw部分有些许CUDA加速代码变动,并使用time记录计算时间
from time import perf_counter
import matplotlib.pyplot as plt
import torch
def Produce_X(x):
x0 = torch.ones(x.numpy().size)
X = torch.stack((x, x0), dim=1)
return X
x = torch.linspace(-3, 3, 100000)
X = Produce_X(x)
Y = x + 1.2 * torch.rand(x.size()) # 与x相同个数的随机数
w = torch.rand(2)
plt.scatter(x.numpy(), Y.numpy(), s=0.001)
plt.show()
# 开启gpu加速训练
CUDA = torch.cuda.is_available()
if CUDA:
print("CUDA success")
inputs = X.cuda()
target = Y.cuda()
w = w.cuda()
w.requires_grad = True
else:
print("CUDA fail")
inputs = X
target = Y
w = w
w.requires_grad = True
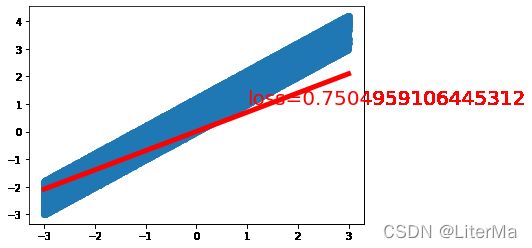
def draw(output, loss):
if CUDA:
output = output.cpu() # 若使用了CUDA加速这一步要还原为CPU数据类型
plt.cla()
plt.scatter(x.numpy(), Y.numpy())
plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5) # 红色,宽度5
plt.text(1, 1, 'loss=%s' % (loss.item()), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.005)
# 训练
def train(epochs=1, learning_rate=0.01):
global loss
for epoch in range(epochs):
output = inputs.mv(w)
loss = (output - target).pow(2).sum() / 100000 # 将均方误差除以数据个数
loss.backward()
w.data -= learning_rate * w.grad
w.grad.zero_() # 调用zero_函数清空grad属性值,避免grad值持续积累
if epoch % 2000 == 0: # 每80个epoch
draw(output, loss)
return w, loss
start = perf_counter()
w, loss = train(10000, learning_rate=1e-4)
finish = perf_counter()
time = finish - start
print("计算时间:%s" % time)
print("fina loss:", loss.item())
print("wights", w.data)
CUDA success
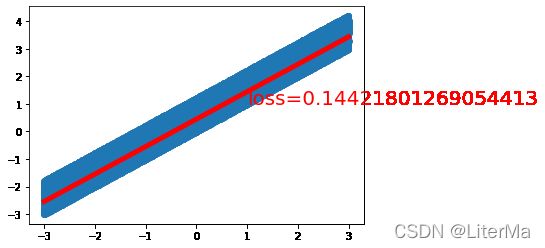
计算时间:9.94497809999666
fina loss: 0.12648160755634308
wights tensor([0.9995, 0.5204], device='cuda:0')
device='cuda:0’指使用显卡的编号,即使用我电脑中唯一一块显卡index为0
神经网络实现线性回归
pytorch已经预先编写好了我们要用到的损失函数以及优化函数
导入所需要的库
import torch
import matplotlib.pyplot as plt
from torch import nn,optim
from time import perf_counter
x=torch.unsqueeze(torch.linspace(-3,3,100000),dim=1)#unsqueeze函数在第一维处增加一个维度
y=x+1.2*torch.rand(x.size())
定义一个LR类继承nn模块中Module,nn是Neural Network的缩写。我们需要在初始化函数时先执行父类的初始化函数,再用nn中预设好的线性的神经网络模块nn.Linear()构造线性模型,Linear()的第一个参数是输入的的维度,第二个参数是输出的维度;接下来在类中定义forward()方法构造向前传播的计算步骤out相当于之前的inputs.mm(w)求出target
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
self.linear = nn.Linear(1, 1) # 因为x与y都是一维的所以设置为(1,1)
def forward(self, x):
out = self.linear(x)
return out
CUDA加速
CUDA = torch.cuda.is_available()
if CUDA:
LR_model = LR().cuda()
inputs = x.cuda()
target = y.cuda()
else:
LR_model = LR()
inputs = x
target = y
画图
def draw(output, loss):
if CUDA:
output = output.cpu() # 若使用了CUDA加速这一步要还原为CPU数据类型
plt.cla()
plt.scatter(x.numpy(), Y.numpy())
plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5) # 红色,宽度5
plt.text(1, 1, 'loss=%s' % (loss.item()), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.005)
nn中自带均方误差函数MSELoss()
数学表达式为
L ( x , y ) = 1 n ∑ ∣ x i − y i ∣ 2 (1-6) L(x,y)=\cfrac{1}{n}\sum\limits\left| x_i-y_i \right|^2\tag{1-6} L(x,y)=n1∑∣xi−yi∣2(1-6)
criterion = nn.MSELoss()
采用随机梯度下降法更新权重,相比梯度下降随机梯度下降法每次随机挑选一个数据样本计算梯度值并进行权值更新,可以避免一次性加载全部数据导致内存溢出,也可以防止梯度下降陷入局部最小值问题。
pytorch中预设的随机梯度下降函数SGD()
第一个是优化神经网络模型的参数,第二个参数是学习率
optimizer = optim.SGD(LR_model.parameters(), lr=1e-4)# parameters()是模型自动产生的参数
编写train()函数
def train(model, criterion, optimizer, epochs):
global loss
for epoch in range(epochs):
output = model(inputs)
# 计算误差
loss = criterion(output, target)
# 清空权重的grad值
optimizer.zero_grad()
# 计算梯度
loss.backward()
# 进行权值更新
optimizer.step()
if epoch % 5000 == 0:
draw(output, loss)
return model, loss
开始训练并计算时间
start = perf_counter()
LR_model, loss = train(LR_model, criterion, optimizer, epochs=10000)
finish = perf_counter()
time = finish - start
print("running time:%s" % time)
print("final loss:", loss.item())
print("wights:", list(LR_model.parameters()))
running time:12.47020970000085
final loss: 0.1208675354719162
wights: [Parameter containing:
tensor([[0.9995]], device='cuda:0', requires_grad=True), Parameter containing:
tensor([0.5789], device='cuda:0', requires_grad=True)]
非线性回归
实际中大多数现象都不是线性的是非线性的,即拟合函数不是直线或平面而是复杂的曲线或曲面。
激活函数
激活函数 f f f实际是一种非常简单的非线性函数,当多个带激活函数的神经元组合在一起就具有拟合复杂非线性函数的能力常用激活函数有:
- sigmoid:
- tanh
- ReLU
- Maxout|
这里我们一般使用ReLU
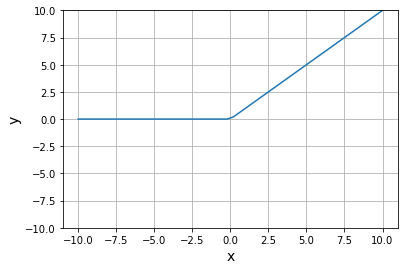
f ( x ) = { 0 , x ⩽ 0 x , x > 0 (2-1) f(x)=\begin{cases}0,&x\leqslant0\\x,&x>0\end{cases}\tag{2-1} f(x)={0,x,x⩽0x>0(2-1)
#画ReLU函数的图像
import matplotlib.pyplot as plt
import torch
x=torch.linspace(-10,10,50)
plt.plot(x,torch.nn.functional.relu(x))
plt.grid()
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.ylim(-10,10)
plt.show()
所以整个人工神经元的数据计算过程为:
y = f ( x → ⋅ w → ) (2-2) y=f(\overrightarrow{x}\cdot \overrightarrow{w})\tag{2-2} y=f(x⋅w)(2-2)
人工神经网络
为研究方便,我们将人工神经网络分为三层:作为输入的神经元结点称为输入层;中间无论多少层都称为隐含层;最后一层作为输出的神经元结点称为输出层。隐含层越复杂,所拟合的非线性函数就越复杂。隐含层大于等于2的神经网络称为深度神经网络。
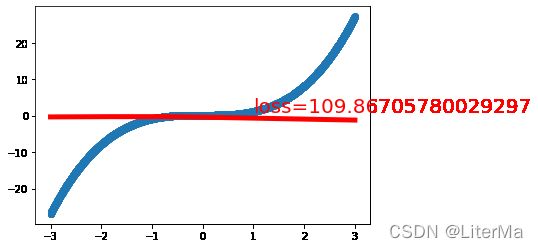
用pyhton据一元三次方程生成一批数据,之后根据这些样本演示神经网络非线性回归:
import matplotlib.pyplot as plt
import torch
x = torch.unsqueeze(torch.linspace(-3, 3, 10000), dim=1) # 1*10000变为1*10000*1
y=x.pow(3)+0.3*torch.rand(x.size())
plt.scatter(x.numpy(),y.numpy(),s=0.01)
plt.show()
由10000个样本绘制出的图像整体呈幂函数分布
对该非线性数据进行拟合,定义一个只有一层隐含的神经网络,构造一个Net类继承nn.Module,前向传播过程中经隐含层self.hidden的数据要经过ReLU激活函数进行非线性处理最后经过输出层。
import matplotlib.pyplot as plt
import torch
from torch import nn, optim
import torch.nn.functional as F
class Net(nn.Module):
# 参数分别为输入维数,隐含层节点数,输出维数
def __init__(self, input_feature, num_hidden, outputs):
super(Net, self).__init__()
#一层隐含层
self.hidden = nn.Linear(input_feature, num_hidden) # 隐含层
#一层输出层
self.out = nn.Linear(num_hidden, outputs) # 输出层,要进行ReLU函数进行非线性处理
# 向前传播
def forward(self, x):
# 激活函数处理数据
x = F.relu(self.hidden(x))
# 结果输出线性叠加
x = self.out(x)
return x
#画图函数
def draw(output, loss): #
if CUDA:
output = output.cpu() # 若使用了CUDA加速这一步要还原为CPU数据类型
plt.cla()
plt.scatter(x.numpy(), y.numpy())
plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=5) # 红色,宽度5
plt.text(1, 1, 'loss=%s' % (loss.item()), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.005)
CUDA加速处理,误差函数和优化器
CUDA = torch.cuda.is_available()
if CUDA:
# 输入1维,隐含节点数20,输出1维
net = Net(input_feature=1, num_hidden=20, outputs=1).cuda()
inputs = x.cuda()
target = y.cuda()
else:
net = Net(input_feature=1, num_hidden=20, outputs=1)
inputs = x
target = y
# 随机梯度下降
optimizer = optim.SGD(net.parameters(), lr=0.01)
# 误差函数
criterion = nn.MSELoss()
训练
# 训练
def train(model, criterion, optimizer, epochs):
for epoch in range(epochs):
output = model(inputs)
loss = criterion(output, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 5000 == 0:
draw(output, loss)
return model, loss
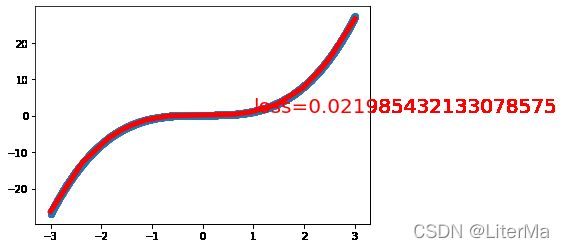
net, loss = train(net, criterion, optimizer, epochs=10000)
详解nn.linear()的原理
print("final loss:", loss.item())
print("hidden weights:", net.hidden.weight)#隐含层参数矩阵
print("hidden bias:", net.hidden.bias)#隐含层每个神经元偏置
print("\n\n-----------------------------------------\n\n")
print("out weights:", net.out.weight)#输出层参数矩阵
print("out bias:", net.out.bias)#输出层偏置
final loss: 0.01662907935678959
hidden weights: Parameter containing:
tensor([[ 1.6169],
[ 0.0310],
[-0.9883],
[-1.5132],
[ 1.4018],
[ 0.1451],
[-1.7884],
[ 0.0049],
[ 1.3800],
[ 0.0910],
[-0.2658],
[-1.2462],
[ 1.3094],
[ 0.1042],
[-0.2192],
[-1.3373],
[ 0.9802],
[-0.7488],
[ 1.7203],
[-1.1895]], device='cuda:0', requires_grad=True)
hidden bias: Parameter containing:
tensor([-3.2474, -0.3090, -1.4296, -1.0454, -3.5876, 0.6779, -4.3901, -0.1257,
-0.8308, -0.4038, 1.0237, -2.4189, -1.2523, 0.6349, 0.7053, -1.5562,
-2.2878, -1.5334, -2.5337, -1.9868], device='cuda:0',
requires_grad=True)
-----------------------------------------
out weights: Parameter containing:
tensor([[ 3.5436, -0.1078, -1.7330, -1.6130, 3.8011, 0.3948, -4.6166, 0.1487,
1.1665, 0.0947, -0.5813, -2.6255, 1.6617, 0.5125, -0.0774, -1.9762,
2.4254, -1.4602, 2.9863, -2.2666]], device='cuda:0',
requires_grad=True)
out bias: Parameter containing:
tensor([0.1983], device='cuda:0', requires_grad=True)
上面的打印代码可由print(list(net.parameters()))代替。
nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)的官方教程:
英文原话:in_features – size of each input sample;out_features – size of each output sample
in_features和out_features是输入和输出的二维大小,bias是偏置b,默认true指b会默认开启学习优化
函数作用是:
y = x A T + b (2-3) y=xA^T+b\tag{2-3} y=xAT+b(2-3)
A指的是该层的参数矩阵,将其逆置后与x做矩阵乘法加上偏置b后作为下一层的输入。
如本例中除去输入层(只是做x的输入,没有做其他事情),就是hidden层和out层,就是代码中该部分:
隐含层
self.hidden = nn.Linear(input_feature, num_hidden)
输出层
self.out = nn.Linear(num_hidden, outputs)
实际上input_feature决定了该层每个神经元中参数 w i w_i wi的个数,output_feature决定了神经元的个数,如本例中hidden层的input_feature为1,output_feature为20,代表输入是1维,隐含层节点有20个。
本例hidden层中参数矩阵
A = [ w 1 w 2 ⋮ w 20 ] A=\begin{bmatrix} w_1\\w_2\\\vdots\\w_{20} \end{bmatrix} A=⎣⎢⎢⎢⎡w1w2⋮w20⎦⎥⎥⎥⎤
b = [ b 1 , b 2 , ⋯ , b 20 ] b=\begin{bmatrix} b_1,&b_2,&\cdots,&b_{20} \end{bmatrix} b=[b1,b2,⋯,b20]
x看做是只有一个元素组成的矩阵或向量,所以nn.linear()按照式子(2-3)做了:
[ x ] A T + b = [ x ] [ w 1 , w 2 , ⋯ , w 20 ] + [ b 1 , b 2 , ⋯ , b 20 ] [x]A^T+b=[x]\begin{bmatrix} w_1,&w_2,&\cdots,&w_{20} \end{bmatrix}+\begin{bmatrix} b_1,&b_2,&\cdots,&b_{20} \end{bmatrix} [x]AT+b=[x][w1,w2,⋯,w20]+[b1,b2,⋯,b20]
根据矩阵相乘原理,x乘上A的转置就是x的行乘上 A T A^T AT的列结果为:
[ x w 1 + b 1 x w 2 + b 2 ⋯ x w 20 + b 2 0 ] \begin{bmatrix} xw_1+b_1&xw_2+b_2&\cdots&xw_{20}+b_20 \end{bmatrix} [xw1+b1xw2+b2⋯xw20+b20]
若令 u i = x w i + b i u_i=xw_i+b_i ui=xwi+bi,再经过ReLU激活函数则输出矩阵为:
[ f ( u 1 ) , f ( u 2 ) , ⋯ , f ( u 20 ) ] \begin{bmatrix} f(u_1),&f(u_2),&\cdots,&f(u_{20}) \end{bmatrix} [f(u1),f(u2),⋯,f(u20)]
待讨论完out层,我们再来研究ReLU激活函数对本例的作用。
得到的结果是1*20的一个矩阵作为输出层的输入,而out层的input_feature和output_feature分别为20和1,代表输入是20维,输出为1维(或是只有一个神经元),out层做了如下处理
y = [ f ( u 1 ) , f ( u 2 ) , ⋯ , f ( u 20 ) ] [ w 1 ′ , w 2 ′ , ⋯ , w 20 ′ ] T + b y=\begin{bmatrix} f(u_1),&f(u_2),&\cdots,&f(u_{20}) \end{bmatrix}\begin{bmatrix}w_1{}',&w_2{}'&,\cdots,&w_{20}'\end{bmatrix}^T+b y=[f(u1),f(u2),⋯,f(u20)][w1′,w2′,⋯,w20′]T+b
得到经神经网络向前传播处理后的结果y,在本例子中y可以写为:
∑ i = 1 , j = 1 20 [ f ( w i + b i ) ] w j + b (2-4) \sum\limits_{i=1,j=1}^{20}[f(w_i+b_i)]w_j+b\tag{2-4} i=1,j=1∑20[f(wi+bi)]wj+b(2-4)
w i w_i wi和 b i b_i bi为hidden的参数, w j w_j wj和 b b b是out层的参数
浅谈ReLU激活函数在本例中的作用
经过上面的讨论我们总结出该例子本质上就是公式(2-4)若忽略 f ( ) f() f()该公式是一个线性公式只能拟合直线,那么为什么它具有拟合曲线的本领呢?
原因在于ReLU函数是一个分段函数
f ( x ) = { 0 , x ⩽ 0 x , x > 0 f(x)=\begin{cases}0,&x\leqslant0\\x,&x>0\end{cases} f(x)={0,x,x⩽0x>0
通过反向传播优化参数我们可以控制结果y在不同区间内呈现不同的直线,就可以让许多直线拟合出曲线的效果,当然参数越多拟合的效果越好,当我们把隐藏层的节点数调的很少,那么我们可以发现拟合结果只有几段的直线,拟合效果会很差。